|
Задачи для подготовки к олимпиадам по математике
(с решениями)
5 класс.
В букете 11 цветов, причем 5 из них – красные, а 6 розы. Какое наибольшее число
белых гвоздик может быть в букете?
Разделите 7 полных, 7 пустых и 7 полупустых бочек меда между тремя купцами, чтобы
всем досталось поровну и бочек и меда. (Мед из бочки в бочку не переливать!)
Известно, что 4 персика, 2 груши и яблоко вместе весят 550 г, аперсик, 3 груши и
яблока вместе весят 450г. Сколько весят персик,груша и яблоко вместе?
Если бы школьник купил 11 тетрадей, то у него осталось бы 5 руб. А на 15 тетрадей у
него не хватило 7 руб. Сколько денег было у школьника?
Отлейте из цистерны 13 л молока, пользуясь бидонами емкостью 17 и 5л.
В четырехэтажном доме Ваня живет выше Пети, но ниже Кати, а Марат живет ниже
Пети. Кто на каком этаже живет
Можно ли заменить несколько минусов на плюсы в равенстве
2004-1-2- 3-4-5-6-7-8=2003 так, чтобы оно стало верным?
В каком числе столько же цифр, сколько букв?
Шесть котов за шесть минут съедают шесть мышей. Сколько понадобится котов, чтобы
за 100 минут съесть 100 мышей?
У меня остановились стенные часы, а никаких других часов у меня нет. Я пошел другу,
часы которого ходят верно, поиграл с ним в шахматы и, придя домой, смог верно
поставить свои часы. Как мне удалось это сделать?
11. В этом примере пропущены два одинаковых числа:
- +8)( :385+9). Какое число пропущено?
12.Изображенную на чертеже фигуру требуется разделить на шесть частей, проведя всего
лишь две прямые.

Инженер ежедневно приезжает поездом на вокзал в 8 ч утра. Точно в 8 ч к вокзалу подъезжает автомобиль и отвозит инженера на завод. Однажды инженер приехал на вокзал в 7 ч утра и пошел навстречу машине. Встретив машину, он сел в нее и приехал на завод на 20 мин раньше, чем обычно. Определить показание часов в момент встречи
инженера с машиной.
Малыш съедает банку варенья за шесть минут, а Карлсон – в два раза
быстрее. За какое время они съедят это варенье вместе?
Для нумерации страниц книги потребовалось всего 1392 цифры.
Сколько страниц в этой книге
6 класс.
Четырех кошек взвесили попарно во всех возможных комбинациях. Получились веса: 7, 8, 9, 10, 11 и 12 кг. Определите общий вес всех четырех кошек.
Из четырех жертвователей второй дал вдвое больше монет, чем первый, третий – втрое больше, чем второй, четвертый – вчетверо больше, чем третий, а все вместе они дали 132 монеты. Сколько монет дал третий жертвователь?
Мотоциклист и велосипедист выехали одновременно из пункта А в пункт В. Проехав треть пути, велосипедист остановился и поехал дальше лишь тогда, когда мотоциклисту осталось проехать треть пути до пункта В. Мотоциклист, доехав до пункта В, сразу поехал обратно. Кто приедет раньше: мотоциклист в пункт А или велосипедист в пункт В?
Над озерами летели гуси. На каждом озере садилась половина гусей и еще полгуся, остальные летели дальше. Все сели на 7 озерах. Сколько было гусей?
Отрежьте от шнура длиной 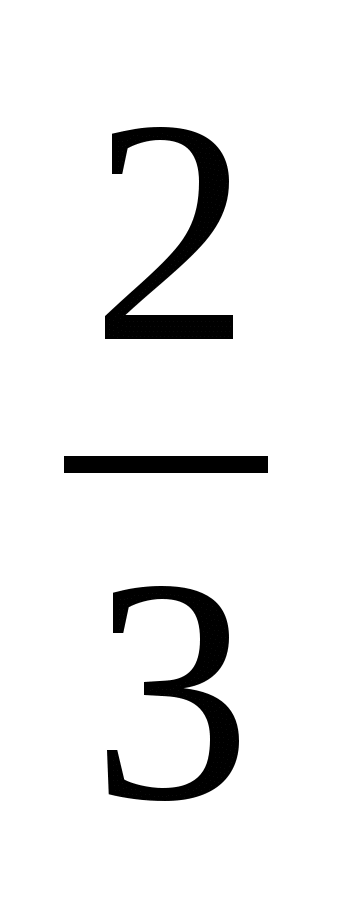 м кусок длиной полметра, не пользуясь линейкой. м кусок длиной полметра, не пользуясь линейкой.
Два мудреца написали на семи карточках числа от 5 до 11. После этого они перемешали карточки, первый мудрец взял себе три карточки, второй взял две, а две оставшиеся карточки они спрятали в мешок. Изучив свои карточки, первый мудрец сказал второму: «Я знаю, что сумма чисел на твоих карточках четна!» Какие числа написаны на карточках первого мудреца?
Коля поймал за 5 дней 512 мух. Каждый день он отлавливал столько мух, сколько во все предыдущие дни вместе. Сколько мух поймал он за каждый из этих дней?
Андрей, Борис, Вадим и Геннадий заняли первые четыре места в соревновании по перетягиванию каната. На вопрос корреспондента, какое место занял каждый из них было получено три ответа: 1) Андрей – первый, Борис – второй, 2) Андрей – второй, Геннадий – третий, 3) Вадим – второй, Геннадий – четвертый. В каждом из этих ответов часть правдива, а вторая ложна. Кто занял какое место?
В ящике лежат 35 шариков. Двое играющих по очереди вынимают их из ящика, причем по условию игры каждый обязан вынуть в свой ход не менее одного шарика и не более пяти. Проигравшим считается тот, кто вынужден будет своим ходом вынуть из ящика последний шар. Может ли игрок, делающий ход первым, обеспечить себе выигрыш? Каким образом?
Мимо железнодорожной станции за известный промежуток времени прошли три поезда. В первом поезде было 418 пассажиров, во втором – 494, в третьем – 456. Узнать, сколько пассажирских вагонов в каждом поезде, если известно, что в каждом вагоне по одинаковому числу пассажиров и число их наибольшее из всех возможных.
У змея Горыныча 2000 голов. Сказочный богатырь одним ударом отрубает 1, 17, 21 или 33 головы, но при этом, соответственно, вырастают 10, 14, 0 или 48 голов. Если все головы отрублены, то новые не отрастают. Сможет ли богатырь победить змея?
В трех ящиках лежат орехи. В первом на 6 орехов меньше, чем в двух других вместе, а во втором – на 10 меньше, чем в первом и третьем вместе. Сколько орехов в третьем ящике?
Числа a и b – целые. Известно, что a+b=2004. Может ли сумма 7a+3b равняться 6799?
Составьте из цифр 1, 2, 3, 4. 5, 6, 7, 8, 9 три трехзначных числа так, чтобы сумма двух чисел равнялась третьему числу и при этом у одного из этих чисел цифра десятков была равна 8 (каждую цифру нужно использовать один раз).)
Игра-лотерея проводится следующим образом. Выбирается случайное число от 1 до 1000. Если оно делится на 2, платят один рубль, если делится на 10 – два рубля, на 12 – четыре рубля, на 20 – восемь, если же оно делится на несколько этих чисел, то платят сумму. Сколько можно выиграть (за один раз) в такой игре?(
7 класс.
После того, как на борт были подняты 30 потерпевших кораблекрушение, оказалось, что запасов питьевой воды, имеющейся на корабле, хватит только на 50 дней, а не на 60, как раньше. Сколько людей было на корабле сначала?
Четверо купцов заметили, что если они сложатся без первого купца, то соберут 90 руб., без второго – 85 руб., без третьего – 80 руб., без четвертого – 75 руб. Сколько у кого денег?
Можно ли перенумеровать ребра куба числами от1 до 12 (каждое ребро – своим числом), чтобы сумма номеров любых трех ребер, сходящихся в одной вершине, делилась на 3?
Пусть запись a b обозначает наибольшее из чисел 2a и a+b. Решите уравнение b обозначает наибольшее из чисел 2a и a+b. Решите уравнение 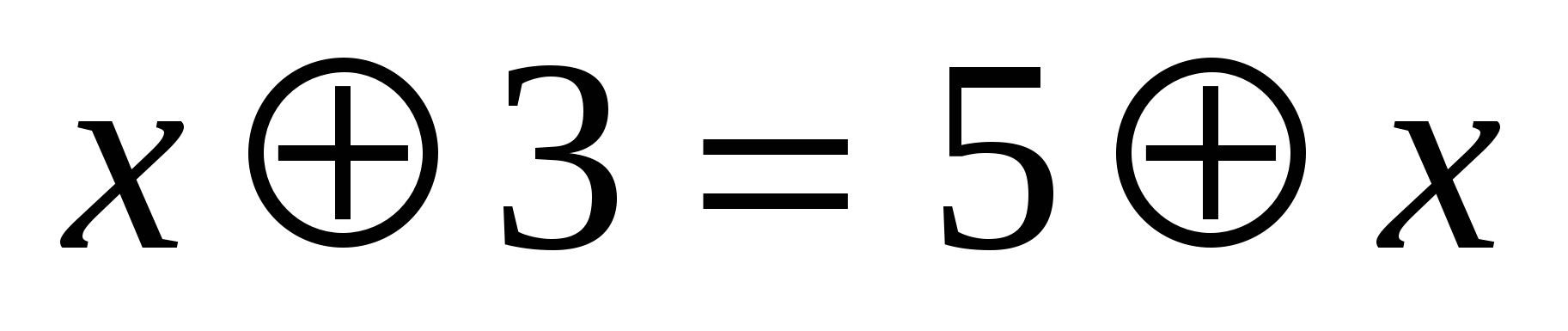 . .
В трех кучках находится 22, 14 и 12 орехов. Требуется путем трех перекладываний уравнять число орехов в каждой кучке, соблюдая при этом условие: из любой кучки разрешается перекладывать в другую лишь столько орехов, сколько их в этой второй кучке.
Вычислите 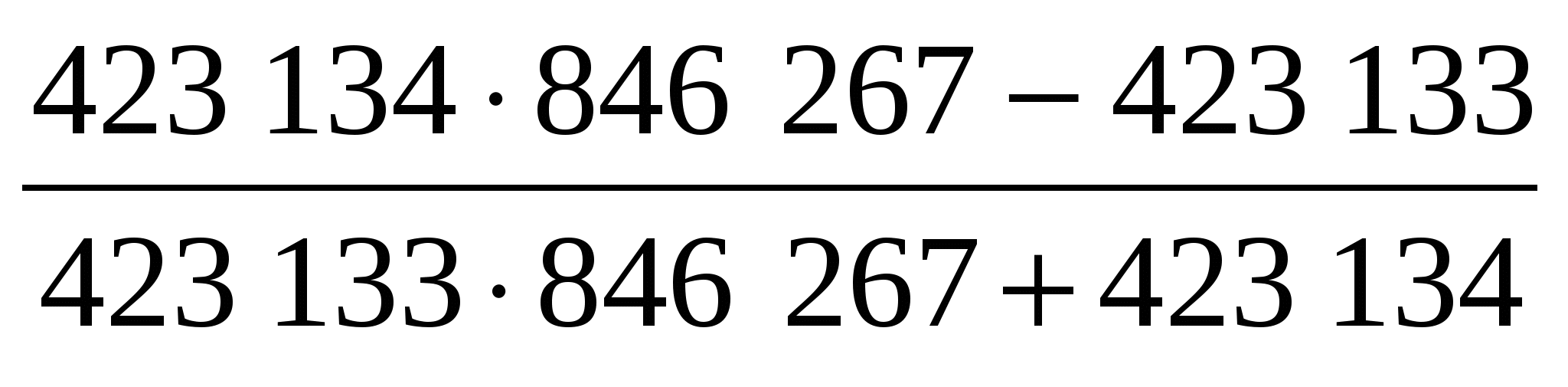 . .
Если полторы курицы несут полтора яйца за полтора дня, то сколько кур плюс еще полкурицы, несущихся в полтора раза быстрее, снесут десяток яиц с половиной за полторы недели?
И сказал Кощей Ивану-царевичу: «Жить тебе, Ваня, до завтрашнего утра. Утром явишься ко предо мною. Задумаю три цифры a, b, c, а ты назовешь мне три числа x, y, z. Выслушаю тебя и скажу, чему равно выражение ax+by+cz. Тогда угадай, какие цифры я задумал. Не угадаешь – голова с плеч…» Опечалился Иван-царевич, пошел думу думать. Нужно бы ему помочь. Как?
Решите уравнение: x-(x-(x-…-(x-1)…))=1 (в записи содержится 2005 пар скобок).
Даны два целых числа a и b. Доказать, что число ab(a+b) – четное.
Из городов А и В навстречу друг другу выехали два автомобиля и встретились через 8 ч. Если бы скорость автомобиля, выехавшего из А, была больше на 14 %, а скорость автомобиля, выехавшего из В, была больше на 15 %, то встреча произошла бы через 7 ч. Скорость какого автомобиля больше и во сколько раз?
Нефтепровод проходит мимо трех деревень А, В, С. В первой деревне сливают 30% от первоначального количества нефти, во второй – 40% того количества, которое дойдет до деревни В, а в третьей – 50% того количества, которое дойдет до деревни С. Сколько процентов нефти от первоначального количества доходит до конца нефтепровода?
Можно ли расставить по кругу числа 14, 27, 36, 57, 178, 467, 590, 2345 так, чтобы любые два соседних числа имели общую цифру?
Даны четыре гири с маркировками: 1, 2, 3 и 4 гр. Одна из них бракованная: более легкая или тяжелая, чем указано. Можно ли за два взвешивания определить, какая гиря бракованная, узнав при этом легче она или тяжелее, чем должна быть?
Сколькими способами можно расставить на полке томики стихов Пушкина, Лермонтова, Некрасова, Маяковского и Пастернака, чтобы Пушкин стоял на первом месте, а Маяковский и Пастернак стояли рядом?
8 класс.
Иван Иванович пришел в магазин, имея 20 рублей. В магазине продавали веники по 1 руб. 17 коп. и тазики по 1 руб. 66 коп. (других товаров в магазине уже не осталось). Сколько веников и сколько тазиков ему нужно купить, чтобы потратить как можно больше денег?
Сократить дробь 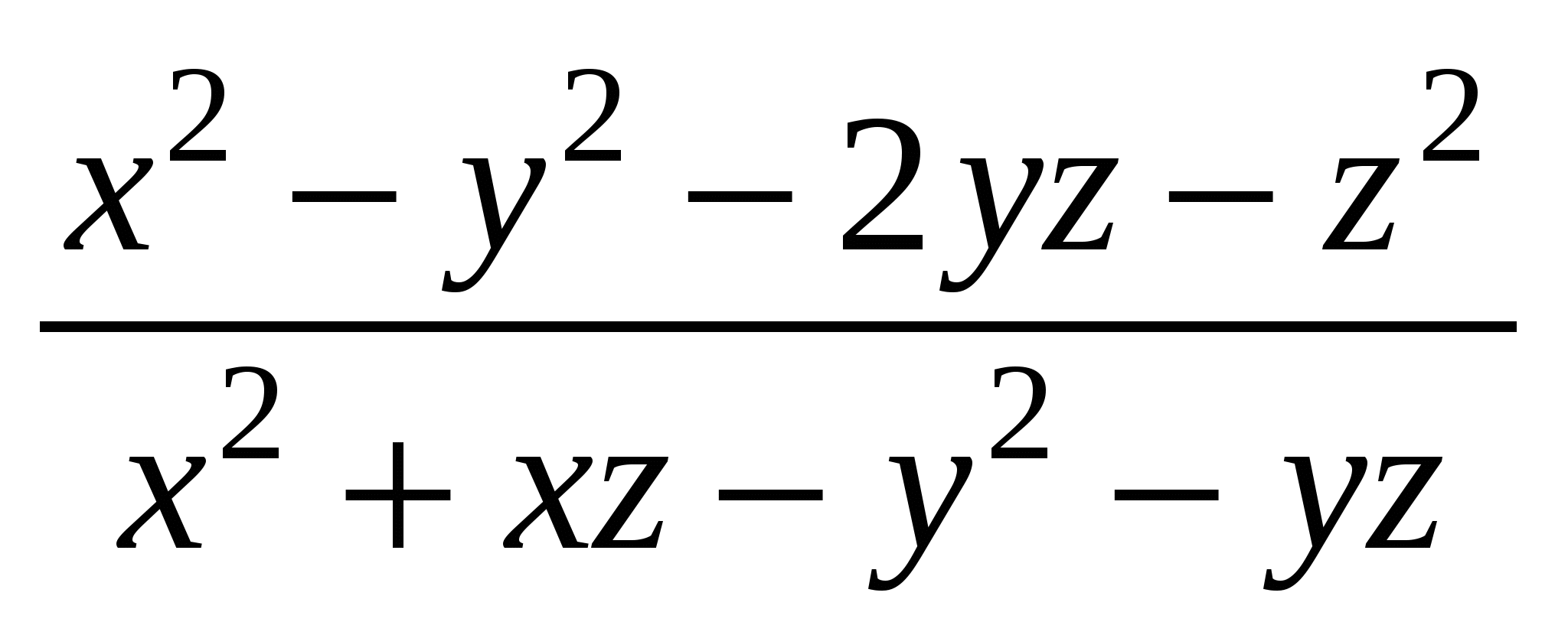 . Из двух городов выезжают по одному направлению два путешественника, первый позади второго. Проехав число дней, равное сумме чисел верст, проезжаемых ими в день, они съезжаются и узнают, что второй проехал 525 верст. Расстояние между городами 175 верст. Сколько верст в день проезжает каждый? . Из двух городов выезжают по одному направлению два путешественника, первый позади второго. Проехав число дней, равное сумме чисел верст, проезжаемых ими в день, они съезжаются и узнают, что второй проехал 525 верст. Расстояние между городами 175 верст. Сколько верст в день проезжает каждый?
На доске была написана обыкновенная несократимая дробь, числитель и знаменатель которой – целые положительные числа. К ее знаменателю прибавили числитель, получилась новая дробь. К числителю новой дроби прибавили ее знаменатель, получилась третья дробь. Когда к знаменателю третьей дроби прибавили числитель, получилось 13/23. Какая дробь была написана на доске? Даны числа 1, 2,3 4, 5, 6. Разрешено к любым двум из них прибавлять по единице. Можно ли за несколько шагов уравнять эти числа?
В одном ящике 50 шариков, а в другом 80. Каждый из двух игроков по очереди вынимает из какого-нибудь ящика любое число шариков. Выиграет тот, который возьмет последний шарик. Тебе разрешается начать игру или предоставить партнеру право первого хода. Как ты будешь играть? Два парома отходят одновременно от противоположных берегов реки и пересекают ее перпендикулярно берегам. Скорости у паромов постоянны. Паромы встречаются друг с другом на расстоянии 720 м от ближайшего берега. Достигнув берега, они сразу отправляются обратно. На обратном пути они встречаются в 400 м от другого берега. Какова ширина реки? Существуют ли целые числа a, b и c, такие, что (3a-b)(3b-c)(3c-a)=5005?
Про два числа x и y известно следующее: 1) если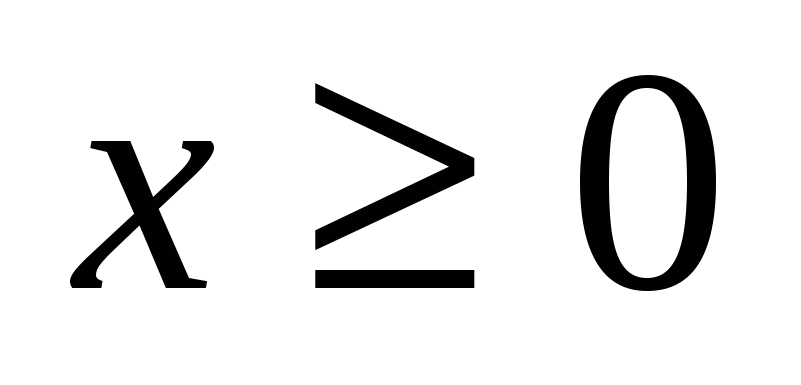 , то , то 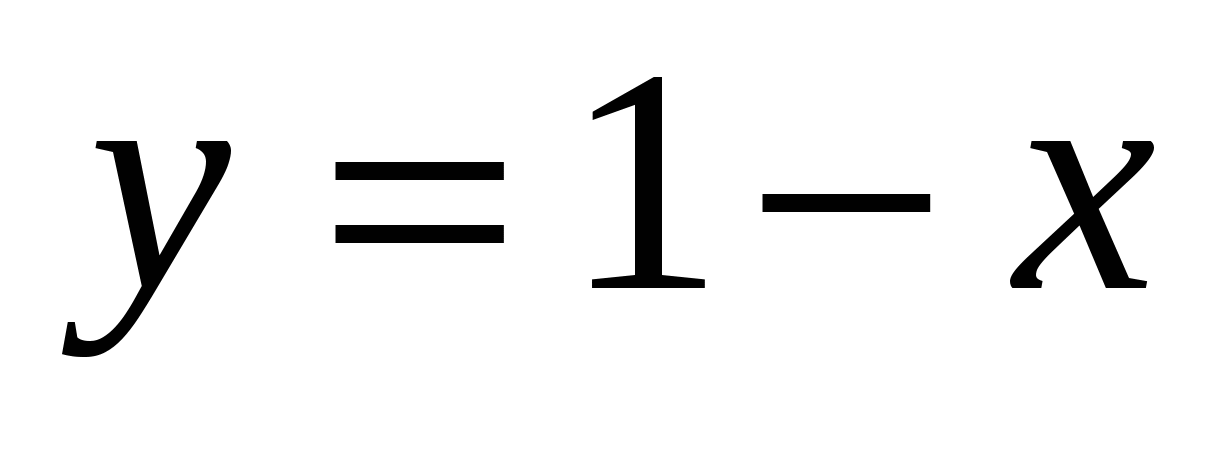 ; 2) если ; 2) если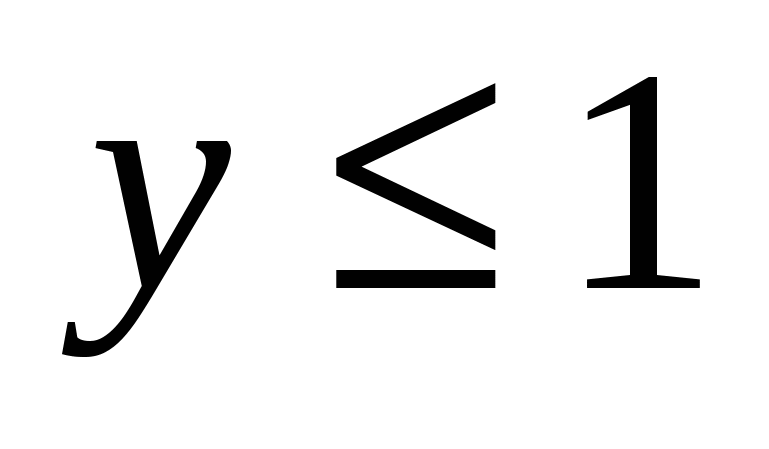 , то , то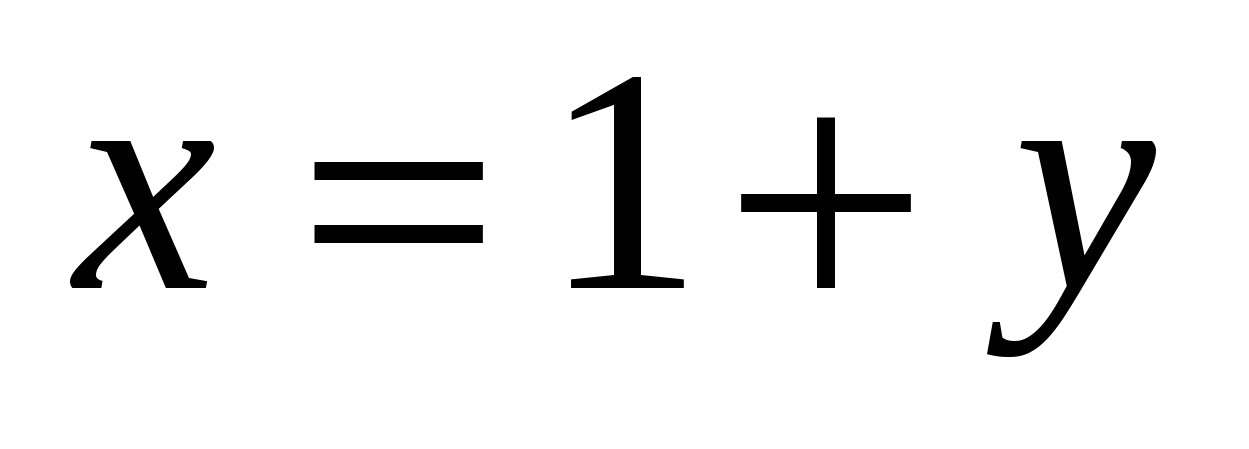 ; 3) если ; 3) если 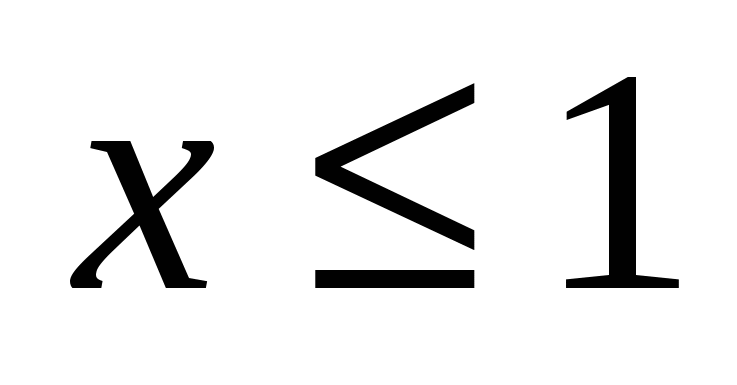 , то , то 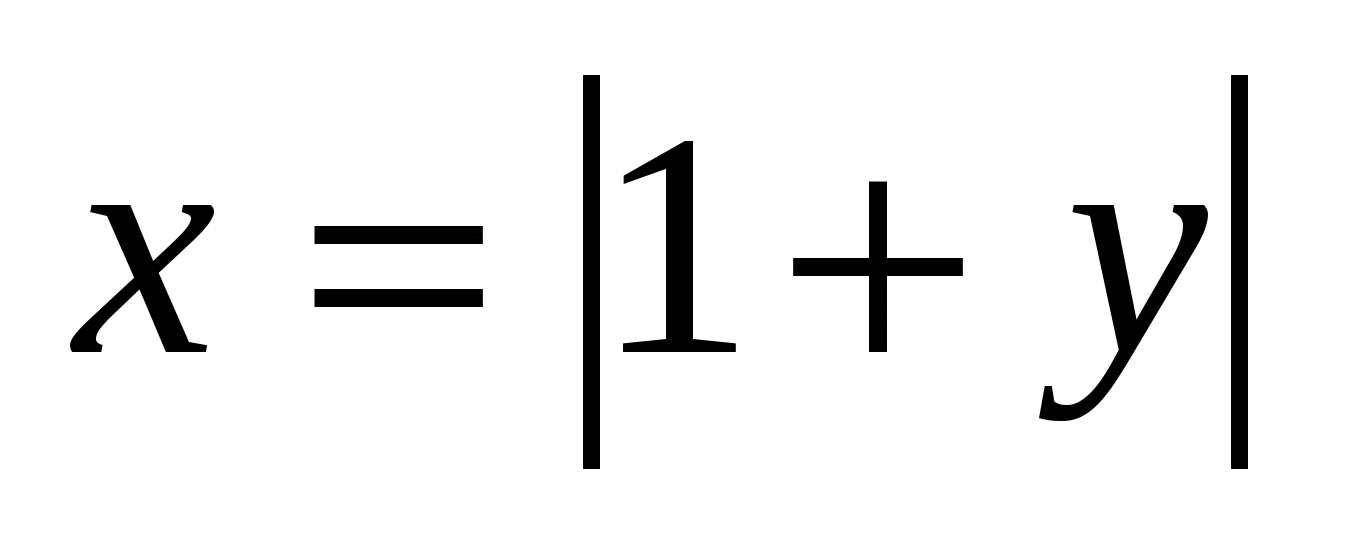 . Найдите x и y. . Найдите x и y.
Имеются бочки весом в 1, 2, 3, 4, …, 19, 20 пудов. Можно ли разложить их в три грузовика поровну (по весу)? Тот же вопрос для бочек весом в 1, 2, 3, …, 9, 10 пудов.
В корзине лежат яблоки и груши. Если добавить туда столько же яблок, сколько сейчас там груш (в штуках), то процент яблок будет вдвое больше, чем получится, если добавить в корзину столько груш, сколько сейчас там яблок. Какой процент яблок сейчас в корзине?
Представьте число 2004 в виде дроби, числителем которой является девятая степень какого-то целого числа, а знаменателем – десятая. Расставьте в таблице 44 10 минусов так, чтобы в каждом столбце было четное число минусов, а в каждой строке – нечетное.
В парке проложена замкнутая дорожка, имеющая вид прямоугольника со сторонами 5м и 3м. По дорожке гуляет дама с собачкой, держа ее на поводке длиной 1м. Нарисуйте участок парка, по которому сможет гулять собачка, не обрывая поводка, если дама обойдет всю дорожку. (Собачка может гулять и внутри, и снаружи дорожки). Сколькими способами хромая ладья может с поля а1 попасть на поле h6, двигаясь только вправо и вверх? Хромая ладья ходит только на одну клетку.
8 класс.
Иван Иванович пришел в магазин, имея 20 рублей. В магазине продавали веники по 1 руб. 17 коп. и тазики по 1 руб. 66 коп. (других товаров в магазине уже не осталось). Сколько веников и сколько тазиков ему нужно купить, чтобы потратить как можно больше денег?
Сократить дробь 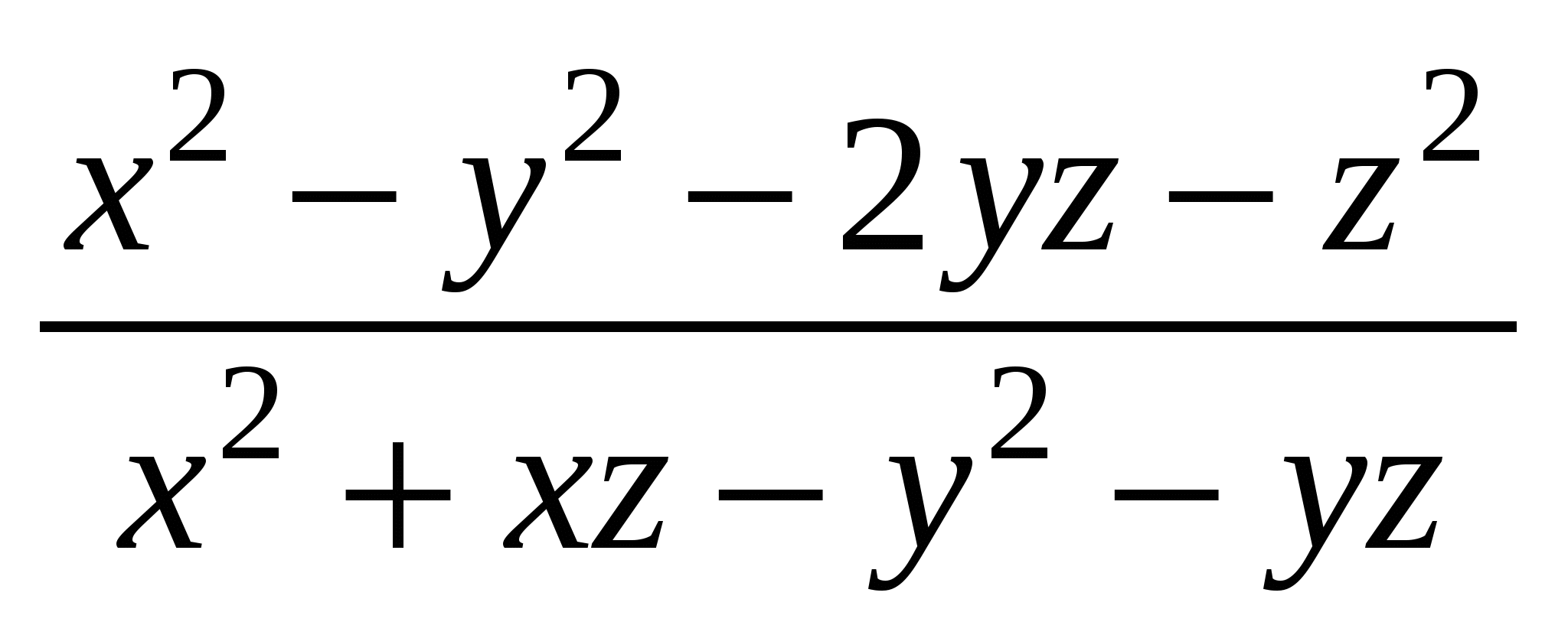 . Из двух городов выезжают по одному направлению два путешественника, первый позади второго. Проехав число дней, равное сумме чисел верст, проезжаемых ими в день, они съезжаются и узнают, что второй проехал 525 верст. Расстояние между городами 175 верст. Сколько верст в день проезжает каждый? . Из двух городов выезжают по одному направлению два путешественника, первый позади второго. Проехав число дней, равное сумме чисел верст, проезжаемых ими в день, они съезжаются и узнают, что второй проехал 525 верст. Расстояние между городами 175 верст. Сколько верст в день проезжает каждый?
На доске была написана обыкновенная несократимая дробь, числитель и знаменатель которой – целые положительные числа. К ее знаменателю прибавили числитель, получилась новая дробь. К числителю новой дроби прибавили ее знаменатель, получилась третья дробь. Когда к знаменателю третьей дроби прибавили числитель, получилось 13/23. Какая дробь была написана на доске? Даны числа 1, 2,3 4, 5, 6. Разрешено к любым двум из них прибавлять по единице. Можно ли за несколько шагов уравнять эти числа?
В одном ящике 50 шариков, а в другом 80. Каждый из двух игроков по очереди вынимает из какого-нибудь ящика любое число шариков. Выиграет тот, который возьмет последний шарик. Тебе разрешается начать игру или предоставить партнеру право первого хода. Как ты будешь играть?
Два парома отходят одновременно от противоположных берегов реки и пересекают ее перпендикулярно берегам. Скорости у паромов постоянны. Паромы встречаются друг с другом на расстоянии 720 м от ближайшего берега. Достигнув берега, они сразу отправляются обратно. На обратном пути они встречаются в 400 м от другого берега. Какова ширина реки? (
Существуют ли целые числа a, b и c, такие, что (3a-b)(3b-c)(3c-a)=5005?
Про два числа x и y известно следующее: 1) если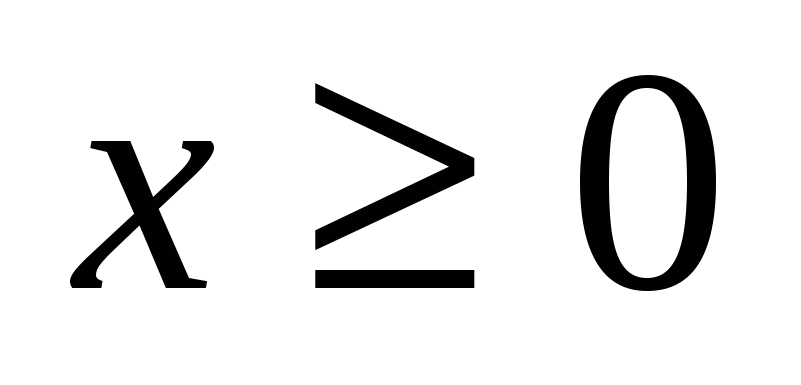 , то , то 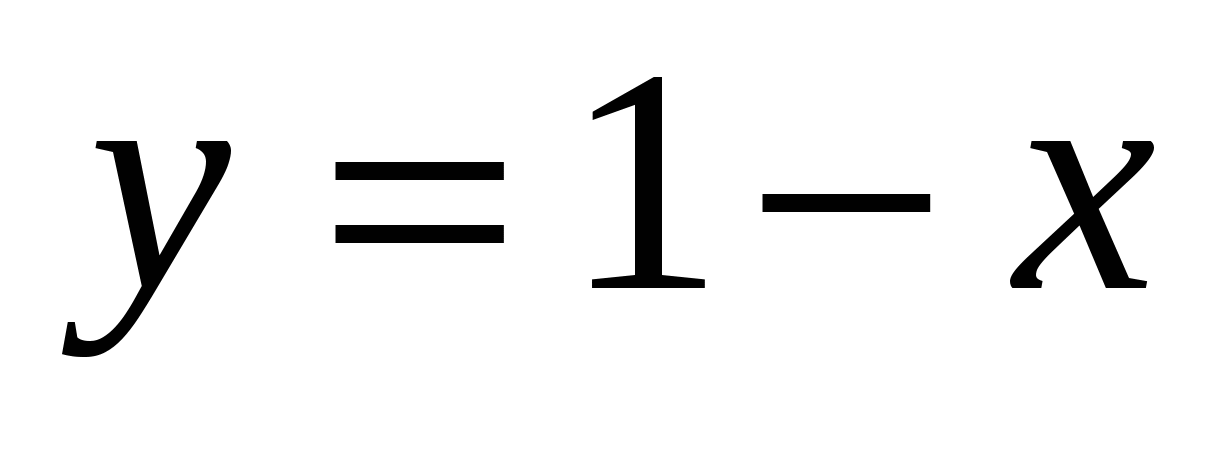 ; 2) если ; 2) если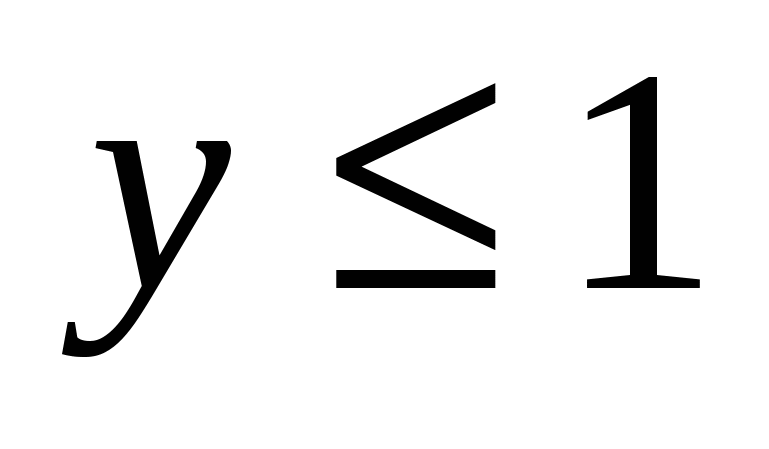 , то , то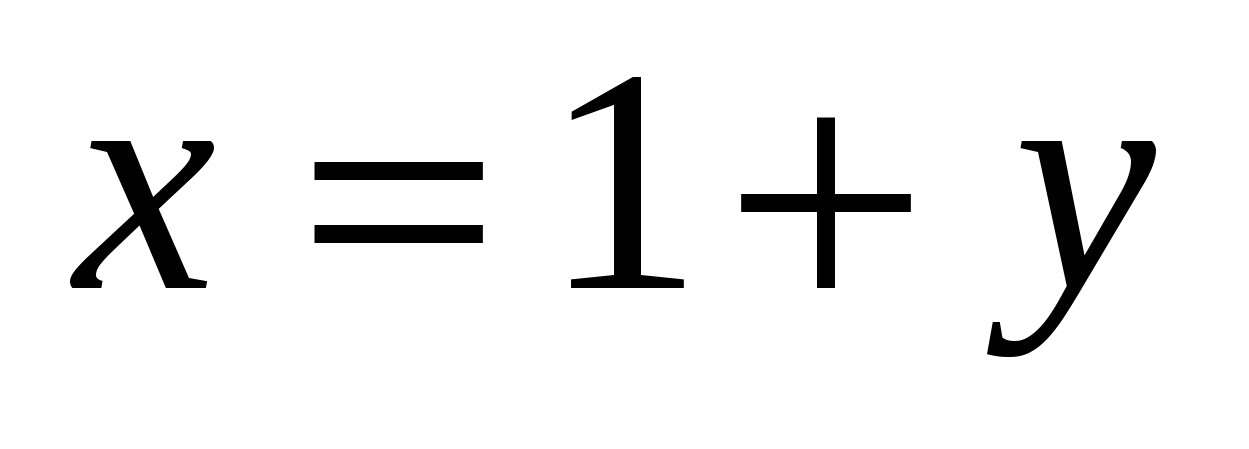 ; 3) если ; 3) если 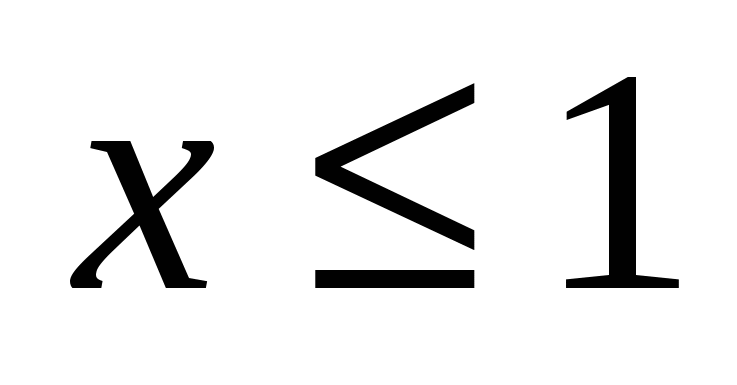 , то , то 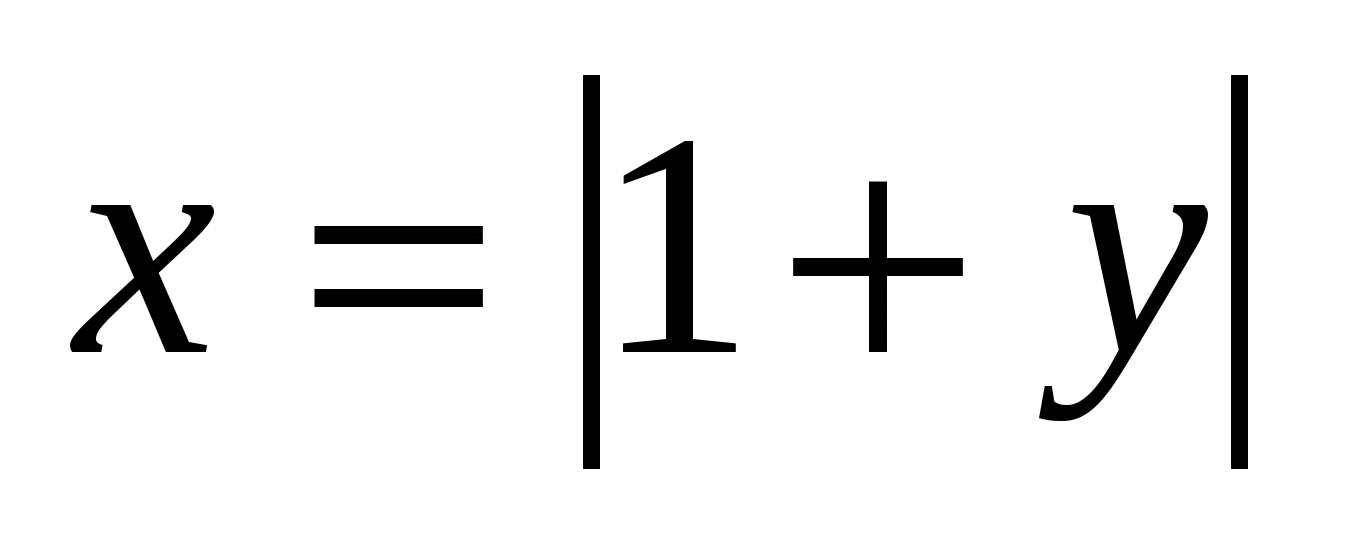 . Найдите x и y. 17. Имеются бочки весом в 1, 2, 3, 4, …, 19, 20 пудов. Можно ли разложить их в три грузовика поровну (по весу)? Тот же вопрос для бочек весом в 1, 2, 3, …, 9, 10 пудов. . Найдите x и y. 17. Имеются бочки весом в 1, 2, 3, 4, …, 19, 20 пудов. Можно ли разложить их в три грузовика поровну (по весу)? Тот же вопрос для бочек весом в 1, 2, 3, …, 9, 10 пудов.
18. В корзине лежат яблоки и груши. Если добавить туда столько же яблок, сколько сейчас там груш (в штуках), то процент яблок будет вдвое больше, чем получится, если добавить в корзину столько груш, сколько сейчас там яблок. Какой процент яблок сейчас в корзине?
19. Представьте число 2004 в виде дроби, числителем которой является девятая степень какого-то целого числа, а знаменателем – десятая.
20. Расставьте в таблице 44 10 минусов так, чтобы в каждом столбце было четное число минусов, а в каждой строке – нечетное.
21. В парке проложена замкнутая дорожка, имеющая вид прямоугольника со сторонами 5м и 3м. По дорожке гуляет дама с собачкой, держа ее на поводке длиной 1м. Нарисуйте участок парка, по которому сможет гулять собачка, не обрывая поводка, если дама обойдет всю дорожку. (Собачка может гулять и внутри, и снаружи дорожки).
Сколькими способами хромая ладья может с поля а1 попасть на поле h6, двигаясь только вправо и вверх? Хромая ладья ходит только на одну клетку.
10 класс.
1. Можно ли разрезать арбуз на 4 части так, чтобы после того, как его съели, осталось 5 корок?
2. В таблице 2 х 2 стоят четыре натуральных числа. Известно, что числа, соседние по вертикали, отличаются на 6, а соседние по горизонтали – в два раза. Найдите эти числа (все возможные варианты) и докажите, что других нет.
3. Можно ли изготовить прямоугольную коробку площади не больше 16, чтобы в нее можно было поместить два пирожных (см. рис.)? Каждое пирожное состоит из пяти квадратов 1 х 1 в форме креста.

4. a, b, c, d – стороны четырехугольника в порядке обхода. Докажите, что его площадь не превосходит (ac+bd)/2.
5. Существуют ли на плоскости четыре точки, попарные расстояния между которыми равны 1, 3, 4, 5, 7 и 8 см?
6. На базаре продаются рыбки, большие и маленькие. Сегодня три больших и одна маленькая стоят вместе столько же, сколько пять больших стоили вчера, а две большие и одна маленькая сегодня – столько же, сколько три больших и одна маленькая вчера. Можно ли по этим данным выяснить, что дороже: одна большая и две маленькие сегодня, или пять маленьких вчера?
7. Можно ли на клетчатой бумаге закрасить 25 клеток так, чтобы у каждой из них было четное число закрашенных соседей?
8. Вырежьте из квадрата 13 х 13 наибольшее количество прямоугольников 1 х 5.
9. Стороны нескольких прямоугольников параллельны осям координат. Любые два из них имеют общую точку. Докажите, что все они имеют общую точку.
10. По прямой летят с равными скоростями 10 одинаковых шариков: 5 слева и 5 справа. После столкновения шарики летят с теми же скоростями в противоположные стороны. Сколько всего произошло столкновений?
11. Доказать, что при всех натуральных n n3+5n делится на 6.
12. В ряд выписано 2005 чисел. Первое число равно 1. Известно, что каждое число, кроме первого и последнего, равно сумме двух соседних. Найти последнее число.
13. На плоскости проведено n прямых. Каждая пересекается ровно с 2004 другими. Чему может быть равно n?
14. Дано 17 чисел. Сумма любых четырех из них положительна. Докажите, что сумма их всех тоже положительна.
15. В народной дружине 100 человек, и каждый вечер трое из них идут на дежурство. Может ли через некоторое время оказаться так, что каждый дежурил с каждым ровно один раз?
-
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
баллы
|
3
|
3
|
3
|
5
|
3
|
3
|
3
|
3
|
4
|
3
|
3
|
3
|
5
|
3
|
3
|
11 класс.
1. Альпинист должен спуститься с вершины отвесной скалы высотой 300 м. На высоте 100 м и 200 м есть площадки, на которых он может остановиться. В распоряжении альпиниста есть веревка длиной 180 м, он может её отрезать, прикреплять к скале (к вершине или на уровне любой площадки), вязать любые узлы, но не может снизу взять веревку, если она где-то выше прибита к скале. Разработайте план действий альпиниста.
2. В таблице 3 х 3 расставлены положительные числа. Произведение чисел в каждой строке и в каждом столбце равно 1, а произведение чисел в любом квадрате 2 х 2 равно 2. Какое число стоит в центре?
3. На плоскости даны треугольник ABC и такие точки D и E, что ADB=BEC=900. Докажите, что длина отрезка DE не превосходит полупериметра треугольника ABC.
4. Прямоугольник разрезан на несколько прямоугольников, периметр каждого из которых – целое число метров. Обязательно ли периметр исходного прямоугольника – тоже целое число метров?
5. Даны числа 1, 2, 3, 4, 5, 6. Разрешается к любым двум числам добавить по единице. Можно ли за несколько таких действий все числа сделать равными?
6. Пешеход шел 3,5 часа, причем за каждый промежуток времени в один час он проходил ровно 5 км. Мог ли он за это время пройти больше 17,5 км?
7. Можно ли расположить на координатной плоскости прямоугольный треугольник с целыми сторонами так, что координаты всех его вершин целые, и ни одна сторона не параллельна осям координат?
8. Четыре населенных пункта находятся в вершинах квадрата со стороной 4 см. Как соединить их системой дорог, имеющей длину не более 11 км, так, чтобы из любого населенного пункта можно было добраться в любой из остальных по этим дорогам?
9. Отметьте несколько точек и несколько прямых так, чтобы на каждой прямой лежало ровно три отмеченные точки и через каждую точку проходило ровно три отмеченные прямые.
10. Сколько существует пятизначных четных чисел, в записи которых есть хотя бы одна тройка?
11. Можно ли расставить в вершинах куба натуральные числа так, чтобы в каждой паре чисел, связанных ребром, одно из них делилось на другое, а во всех других парах такого не было?
12. Правильный 2005-угольник разбит непересекающимися диагоналями на треугольники. Докажите, что среди них ровно один остроугольный.
13. На какое наименьшее число прямоугольников можно разрезать фигуру (см. рис.)? Резать можно только по границам клеток.
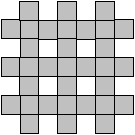
14. Три мухи сели в полдень на секундную, минутную и часовую стрелки и поехали на них. Когда какая-то стрелка обгоняла другую, сидящие на этих стрелках мухи менялись местами (а если бы секундная стрелка обогнала часовую и минутную стрелки одновременно, то местами поменялись бы мухи с секундной и часовой стрелок). Сколько кругов проехала каждая из мух до полуночи?
15. Известно, что a+b+c=5, ab+ac+bc=7. Найти a2+b2+c2. |
 Скачать 491.03 Kb.
Скачать 491.03 Kb.