Урок повторения Теория вероятности очень сложный предмет, если рассматривать отдельно
 Скачать 143.21 Kb. Скачать 143.21 Kb.
|
 ЗАДАЧА В10 Теория Вероятности. (Урок повторения) Теория вероятности – очень сложный предмет, если рассматривать отдельно. Но на ЕГЭ надо знать только самые основные понятия теории вероятностей. Если вы их будете понимать, то и задача покажется лёгкой. Приступим: 1. Случайное событие (СС)- это событие, которое либо произойдёт, либо нет. В жизни мы постоянно сталкиваемся со случайными событиями. Примеры:
2. Каждое случайное событие (СС) иметь свою вероятность произойти (сбыться, реализоваться). Каждый, думаю, понимает интуитивно, что такое вероятность. Одно событие может произойти со 100%-ой вероятностью, другое почти с нулевой и т.д. Примеры:
3. Испытание – любое действие, которое может привести к одному или нескольким результатам. 4. Исход - конечный результат испытания. Значит испытание может иметь один или несколько исходов. Например:
5. Благоприятный исход - желаемый исход. Примеры:
Какова же связь между этими понятиями? ЗАПОМНИ: 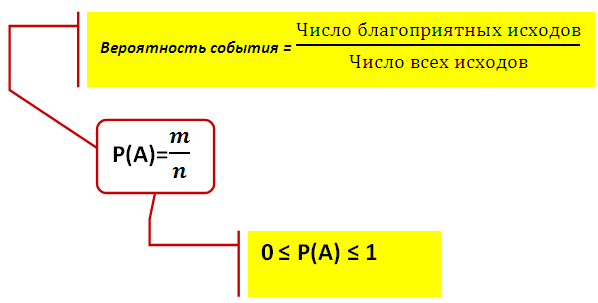 Эта формула называется классической формулой вероятности или классическим определением вероятности. Где:
Рассмотрим тот же пример: Сдаю экзамен. Из 20 билетов 10 знаю на отлично, 5 на хорошо, 3 на удовлетворительно и 2 не знаю. Хочу сдать на хорошо. Тогда благоприятный исход = сдать на хорошо. А какова вероятность сдать на хорошо? Решение:
Заметьте, ответы представлены в десятичной дроби, потому что в бланках ЕГЭ, надо писать в десятичном виде (если не указано иное). Классическая формула вероятности – самая главная и основная. Но бывают затруднения в нахождении n и m. В этом случае надо знать элементы комбинаторики: 1. Теорема о перемножении шансов: Пусть множество А состоит из k элементов, а множество B — из m элементов, тогда можно образовать ровно km пар, взяв первый элемент из множества A, а второй — из множества B. т.е. если первый элемент можно выбрать k способами, а второй элемент — m способами, то пару элементов можно выбрать km способами. Примеры:
Простые задачи на осмысление
подсказка: решение на теорему о перемножении шансов А теперь знакомимся со вторым элементом комбинаторики: 2. Выборы шариков из урны (или кубиков из ящика, или карточек из коробки, или книг с полки, или изделий из партии, или номер при жеребьёвке и т.д.): Есть урна (ящик), содержащая n пронумерованных объектов (шаров). Мы выбираем из этой урны k шаров; результатом выбора является набор из k шаров. Нас интересует, сколькими способами можно выбрать k шаров из n, или сколько различных результатов может получиться? На этот вопрос нельзя дать однозначный ответ, пока мы не определимся: а) с тем, как организован выбор: можно ли шары возвращать в урну, и б) с тем, что понимается под различными результатами выбора: учитывается или нет порядок. Рассмотрим следующие возможные способы выбора: 1) Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. Таким образом, в полученном наборе из k шаров могут встречаться одни и те же. 1.1) Выбор с учётом порядка: например, при выборе трёх шаров из 5, лежащих в урне, наборы (1, 5, 2) и (2, 5, 1) различны, если порядок учитывается. 1.2) Выбор без учёта порядка: т.е. наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Например, наборы (1, 5, 2) и (2, 5, 1) не различаются и образуют один и тот же результат выбора, если порядок не учитывается. 2) Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же шары. 2.1) Выбор с учётом порядка: например, при выборе трёх шаров из 5, лежащих в урне, наборы (1, 5, 2) и (2, 5, 1) различны, если порядок учитывается. 2.2) Выбор без учёта порядка: т.е. наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Например, наборы (1, 5, 2) и (2, 5, 1) не различаются и образуют один и тот же результат выбора, если порядок не учитывается. надо определить чётко: 1. Можно ли шары возвращать в урну (книги на полку, карточки с номерами в коробку для жеребьёвки и т.д.)? 2. Учитывать порядок или нет? Определив это, идём дальше. Скопируйте себе картинку (правая кнопка мыши -> Сохранить картинку как…) и распечатайте как шпаргалку: Шпаргалка:  Символ n! ( называется факториал ) – сокращённая запись произведения: 1 · 2 · 3 · … · ( n – 1 ) ·n . Подробнее о шпаргалке: Размещением k элементов из n (из n элементов по k) называются соединения, которые можно образовать из n элементов, собирая в каждое соединение по k элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения. Перестановка: возьмём n различных элементов: a1 , a2 , a3 , …, an . Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения.Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается Pn . Это число равно произведению всех целых чисел от 1 до n. Сочетание без повторений: число способов выбрать m элементов из n различных элементов (m≤n) без упорядочения. Сочетание с повторениями: число способов разместить m одинаковых элементов (предметов) в n ячейках (ящиках). Чтобы вникнуть в вышеперечисленные понятия, разбери решённые задачи. Задача 1Б. В розыгрыше кубка страны по футболу берут участие 17 команд. Сколько существует способов распределить золотую, серебряную и бронзовую медали? Решение: Поскольку медали не равноценны, то количество способов распределить золотую, серебряную и бронзовую медали среди команд будет равно числу размещений из 17-ти элементов по 3, т.е. = 4080. Задача 2Б. Произведено три выстрела по мишени. Рассматриваются такие элементарные события: А – попадание в мишень при i-том выстреле;  – промах по мишени при i-том выстреле. Выразить через А и – промах по мишени при i-том выстреле. Выразить через А и  следующие события: следующие события:А – все три попадания; В – ровно два попадания; С – все три промаха; D – хотя бы одно попадание; Е – больше одного попадания; F – не больше одного попадания. Решение: А – все три попадания, т.е. совместное появления трех событий А1, А2 и А3 Р(А) = Р(А1 и А2 и А3) В – ровно два попадания, т.е. два попадания и один промах Р(В) = Р(  1 и А2 и А3 или А1 и 1 и А2 и А3 или А1 и  2 и А3 или А1 и 2 и А3 или А1 и  2 и А3) 2 и А3)С – все три промаха, т.е. совместное появления трех событий  1 и 1 и  2, 2,  3 3Р(С) = Р(  1 и 1 и  2 и 2 и  3) 3)D – хотя бы одно попадание, т.е. или одно попадание, или два попадания или три попадания Р(D) = Р(  1 и 1 и  2 и А3 или 2 и А3 или  1 и А2 и 1 и А2 и  3 или А1 и 3 или А1 и  2 и 2 и  3 ИЛИ 3 ИЛИ  1 и А2 и А3 или А1 и 1 и А2 и А3 или А1 и  2 и А3 или А1 и 2 и А3 или А1 и  2 и А3 ИЛИ А1 и А2 и А3) 2 и А3 ИЛИ А1 и А2 и А3) или по формуле Р(D) = 1 – Р(  1 и 1 и  2 и 2 и  3) 3)Е – больше одного попадания, т.е. или два попадания или три попадания Р(Е) = Р(  1 и А2 и А3 или А1 и 1 и А2 и А3 или А1 и  2 и А3 или А1 и 2 и А3 или А1 и  2 и А3 или А1 и А2 и А3) 2 и А3 или А1 и А2 и А3)F – не больше одного попадания, т.е. одно попадание и два промаха Р(F) = Р(  1 и 1 и  2 и А3 или 2 и А3 или  1 и А2 и 1 и А2 и  3 или А1 и 3 или А1 и  2 и 2 и  3) 3)Задача 3Б. Игральный кубик бросают два раза. Описать пространство элементарных событий. Описать события: А – сумма появившихся очков равна 8; В – по крайней мере один раз появится 6. Решение: Будем считать пространством элементарных событий множество пар чисел (i, j), где i (соответственно j) есть число очков, выпавших при первом (втором) подбрасывании, тогда множество элементарных событий будет таким: ={(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)} А – сумма появившихся очков равна 8. Этому событию благоприятствуют такие элементарные события А={(2,6) (6,2) (5,3) (3,5) (4,4)}. В – по крайней мере один раз появится 6. Этому событию благоприятствуют такие элементарные события В={(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) (1,6) (2,6) (3,6) (4,6) (5,6)}. Задача 4. В вазе с цветами 15 гвоздик: 5 белых и 10 красных. Из вазы наугад вынимают 2 цветка. Какова вероятность того, что эти цветки: а) оба белые; б) оба красные; в) разного цвета; г) одного цвета. Решение: а) Пусть событие А состоит в том, что оба вынутых из вазы цветка белые. Количество возможных способов взять 2 цветка из 15-ти равно 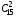 , т.е. , т.е. 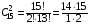 = 715 = 105, а количество возможных способов взять 2 белых цветка из 5-ти белых равно = 715 = 105, а количество возможных способов взять 2 белых цветка из 5-ти белых равно 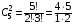 = 25 = 10. Тогда по классическому определению вероятность события А равна = 25 = 10. Тогда по классическому определению вероятность события А равна 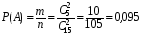 . .б) Пусть событие В состоит в том, что оба вынутых из вазы цветка красные. Количество возможных способов взять 2 цветка из 15-ти равно 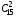 , т.е. , т.е. 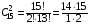 = 715 = 105, а количество возможных способов взять 2 красных цветка из 10-ти красных равно = 715 = 105, а количество возможных способов взять 2 красных цветка из 10-ти красных равно 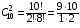 = 95 = 45. Тогда по классическому определению вероятность события В равна = 95 = 45. Тогда по классическому определению вероятность события В равна 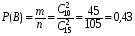 . .в) Пусть событие С состоит в том, что оба вынутых из вазы цветка разного цвета, т.е. один белый и один красный. Количество возможных способов взять 2 цветка из 15-ти равно 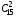 , т.е. , т.е. 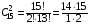 = 715 = 105, а количество возможных способов взять 1 красный цветок из 10-ти красных И 1 белый цветок из 5-ти белых равно = 715 = 105, а количество возможных способов взять 1 красный цветок из 10-ти красных И 1 белый цветок из 5-ти белых равно 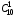 * *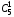 = 105 = 50. Тогда по классическому определению вероятность события С равна = 105 = 50. Тогда по классическому определению вероятность события С равна 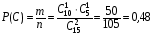 . .г) Пусть событие D состоит в том, что оба вынутых из вазы цветка одного цвета, т.е. или оба белые (событие А) или оба красные (событие В). По теореме сложения независимых событий вероятность события D будет равна Р(D) = Р(А или В) = Р(А) + Р(В) = 0,095 + 0,43 = 0,525 Задача 5. Из шести карточек с буквами I, С, К, Ь, Н, М наугад одну за другой вынимают и раскладывают в ряд в порядке появления. Какова вероятность того, что появится слово а) «НIС»; б) «CIM»? Решение: (для пунктов а) и б) одинаково) Каждый вариант получившегося «слова» является размещением из 6-ти элементов по 3. Число таких вариантов равно 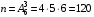 . Из этих вариантов правильным будет только один, т.е. m = 1, тогда по классическому определению вероятности . Из этих вариантов правильным будет только один, т.е. m = 1, тогда по классическому определению вероятности 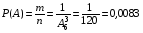 . .Задача 6. Вероятность того, что в течении одной смены возникнет поломка станка равна 0,05. Какова вероятность того, что не возникнет ни одной поломки за три смены? Решение: Пусть событие А состоит в том, что в течении одной смены возникнет поломка станка. По условию задачи вероятность этого события равна Р(А) = 0,05. Противоположное событие  состоит в том, что в течении одной смены поломка станка НЕ возникнет. Вероятность противоположного события Р( состоит в том, что в течении одной смены поломка станка НЕ возникнет. Вероятность противоположного события Р( ) = 1– Р(А) = 1 – 0,05 = 0,95. Искомая вероятность равна Р(В) = Р( ) = 1– Р(А) = 1 – 0,05 = 0,95. Искомая вероятность равна Р(В) = Р( и и  и и  ) = Р( ) = Р( )Р( )Р( )Р( )Р( )= 0,950,950,95 = 0,953 = 0,86 )= 0,950,950,95 = 0,953 = 0,86Задача 7. Студент пришел на зачет зная только 30 вопросов из 50. Какова вероятность сдачи зачета, если после отказа отвечать на вопрос преподаватель задает еще один? Решение: Вероятность того, что преподаватель задал студенту вопрос, на который он не знал ответа (событие А) равна Р(А) = 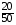 . Найдем вероятность того, что на второй вопрос преподавателя студент знает ответ (событие В) при условии, что ответа на первый вопрос студент не знал. Это условная вероятность, так как событие А уже произошло. Отсюда РА(В) = . Найдем вероятность того, что на второй вопрос преподавателя студент знает ответ (событие В) при условии, что ответа на первый вопрос студент не знал. Это условная вероятность, так как событие А уже произошло. Отсюда РА(В) = 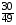 . Искомую вероятность определим по теореме умножения вероятностей зависимых событий. Р(А и В) = Р(А)* РА(В) = . Искомую вероятность определим по теореме умножения вероятностей зависимых событий. Р(А и В) = Р(А)* РА(В) = 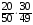 = 0,24. = 0,24.Задача 9. С помощью наблюдений установлено, что в некоторой местности в сентябре в среднем бывает 25 дней без дождя. Какова вероятность того, что 1-го и 2-го сентября дождя не будет? Решение: Вероятность того, что 1-го сентября дождя не будет (событие А) равна Р(А) = 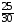 . Найдем вероятность того, что и 2-го сентября дождя не будет (событие В) при условии, что 1-го сентября дождя не было. Это условная вероятность, так как событие А уже произошло. Отсюда РА(В) = . Найдем вероятность того, что и 2-го сентября дождя не будет (событие В) при условии, что 1-го сентября дождя не было. Это условная вероятность, так как событие А уже произошло. Отсюда РА(В) = 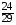 . Искомую вероятность определим по теореме умножения вероятностей зависимых событий. Р(А и В) = Р(А)* РА(В) = . Искомую вероятность определим по теореме умножения вероятностей зависимых событий. Р(А и В) = Р(А)* РА(В) = 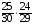 = 0,7. = 0,7.Задача 13. Из партии, в которой 25 изделий, среди которых 6 бракованных, случайным образом выбрали 3 изделия для проверки качества. Найти вероятность того, что: а) все изделия годные, б) среди выбранных изделий одно бракованное; в) все изделия бракованные. Решение: а) Пусть событие А состоит в том, что все выбранные изделия годные. Количество возможных способов взять 3 изделия из 25-ти равно 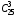 , т.е. , т.е. 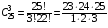 = 2300, а количество возможных способов взять 3 годных изделия из (25 – 6) = 19-ти годных равно = 2300, а количество возможных способов взять 3 годных изделия из (25 – 6) = 19-ти годных равно 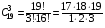 = 1938. Тогда по классическому определению вероятность события А равна = 1938. Тогда по классическому определению вероятность события А равна 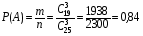 . .б) Пусть событие В состоит в том, что среди выбранных изделий одно бракованное, т.е. одно бракованное и два годных. Количество возможных способов взять 3 изделия из 25-ти равно 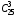 = 2300, а количество возможных способов взять одно бракованное изделие из 6-ти бракованных И два годных изделия из (25 – 6) = 19-ти годных равно = 2300, а количество возможных способов взять одно бракованное изделие из 6-ти бракованных И два годных изделия из (25 – 6) = 19-ти годных равно 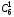 * *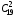 = 6153 = 738. Тогда по классическому определению вероятность события В равна = 6153 = 738. Тогда по классическому определению вероятность события В равна 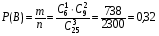 . .в) Пусть событие С состоит в том, что все выбранные изделия бракованные. Количество возможных способов взять 3 изделия из 25-ти равно 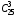 = 2300, а количество возможных способов взять 3 бракованные изделия из 6-ти бракованных равно = 2300, а количество возможных способов взять 3 бракованные изделия из 6-ти бракованных равно 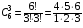 = 20. Тогда по классическому определению вероятность события С равна = 20. Тогда по классическому определению вероятность события С равна 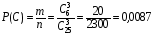 . .Задача 13. В урне находится 6 шаров: 1 белый, 2 красных и 3черных. Наугад вытаскивают 3 шара. Какова вероятность того, что среди вытащенных шаров ровно 1 будет черным? Решение:
Задачи для самостоятельного решения 1. Обезьяна напечатала на машинке слово из десяти букв. Сколько слов (набор букв) она может напечатать? 2. Женя, Петя, Оля и Лена занимают какие-то четыре из десяти мест в классе. Сколькими способами они могут сесть? 3. Найти число возможных результатов подбрасывания трёх игральных костей, если кости считаются неразличимыми. 4. В урне находится 12 белых и 8 черных шаров. Найти вероятность того, что два одновременно изъятых наудачу шара будут черными. На этом урок закончен! Использованы материалы из: https://probno.ru/v10-teoriya-veroyatnosti-novoe/ | |||||||