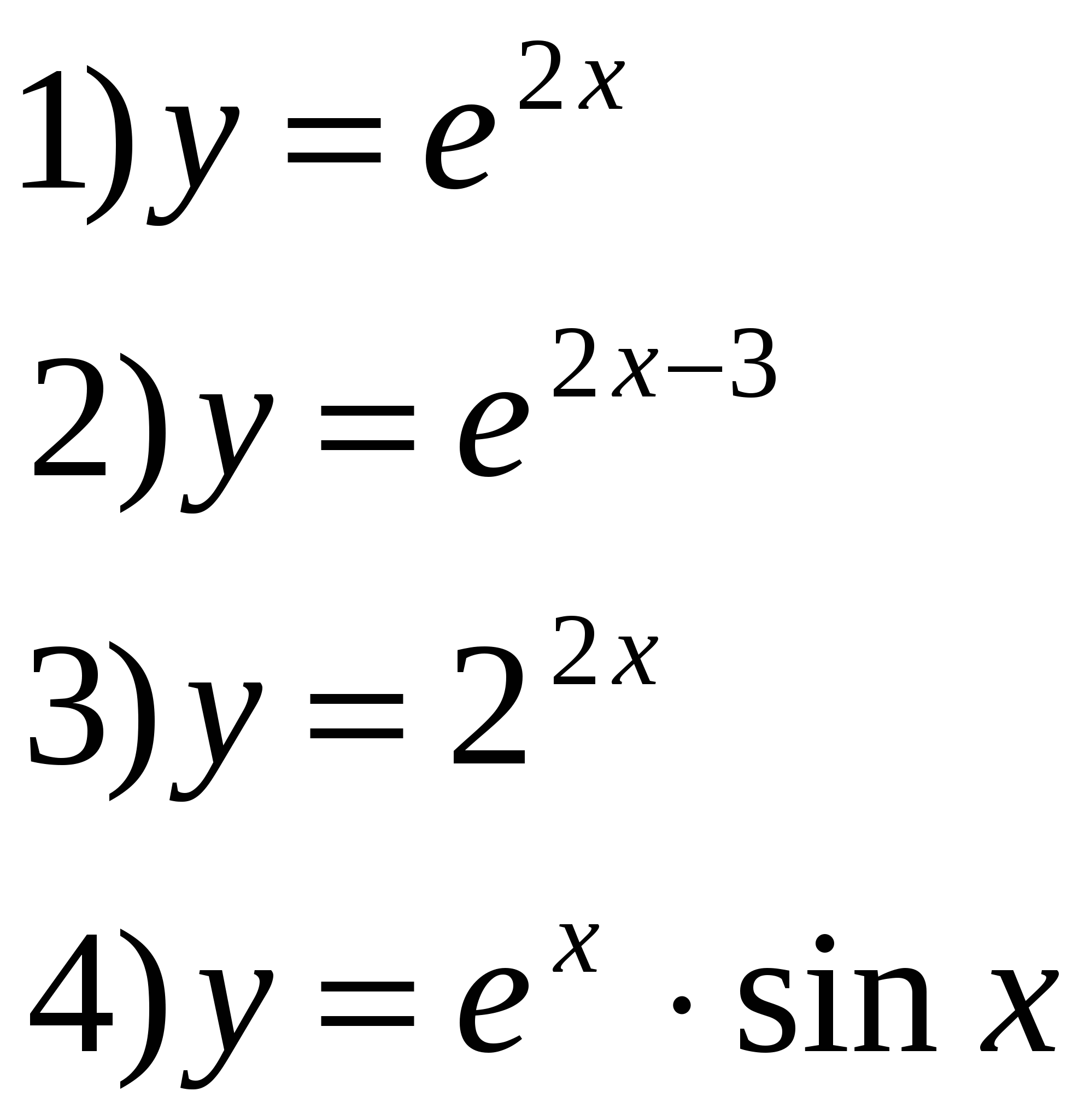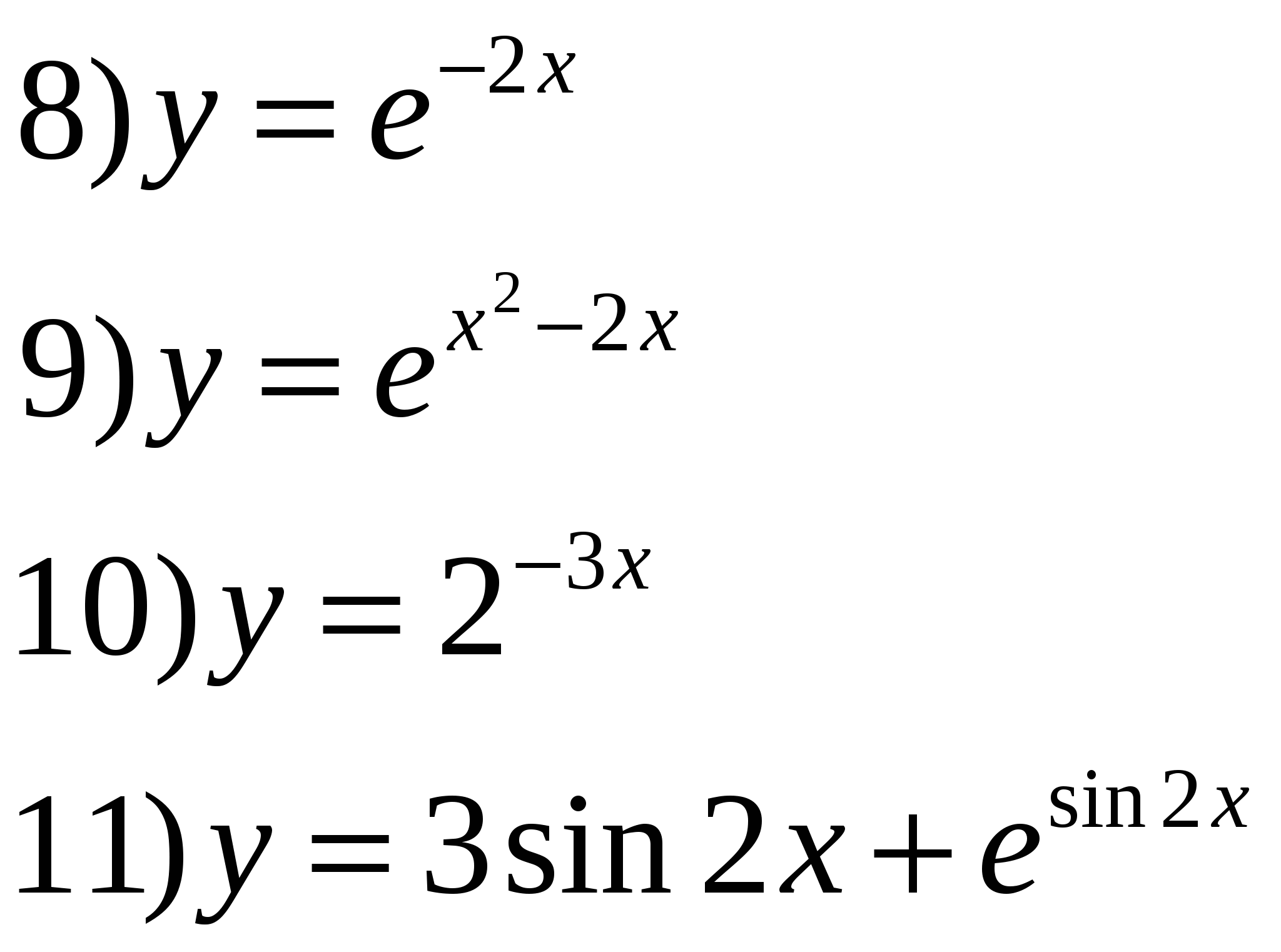Урок по теме: «Производная и первообразная показательной функции»
 Скачать 116.18 Kb.
|
Самоукина Галина Петровна Учитель математики МКОУ « Средняя общеобразовательная школа №1» имени Героя Советского Союза А.С. Шелаева город Киров, Калужская область . Конспект урока Предмет- алгебра и начала анализа. 11 класс Урок по теме: «Производная и первообразная показательной функции» Дата выполнения работы - 2011 год Урок закрепления изученного Предмет: алгебра и начала анализа 11 класс Тема: « Производная и первообразная показательной функции» Цели и задачи:
отношение к учению. При подготовке к уроку была использована литература: 1. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. / Под редакцией А.Н. Колмогорова.-М.: Просвещение, 2008 год. 2. Дидактические материалы по алгебре и началам анализа для 11 класса:/Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. 3. Задачи по алгебре и началам анализа для 10-11 классов / С.М. Саакян, А.М. Гольдман, Д.В. Денисов. Данный авторский материал ранее нигде не публиковался и не размещался. Данный урок – урок закрепления, проводится в нестандартной форме. Чтобы овладеть настоящим, постоянно приходится обращаться к прошлому, а именно: вспомнить график показательной функции, формулу площади криволинейной трапеции, схему исследования функции с помощью производной и др. В каждом классе наряду с хорошо успевающими учащимися присутствуют такие, которым для усвоения материала требуется больше времени. Поэтому на уроке предусмотрена работа по уровням. Кроме того, учащимся предоставляется возможность «расти» в знаниях, поэтому заготавливается достаточное количество дополнительных карточек с заданиями разного уровня и которые оцениваются отдельно. Цели и задачи:
отношение к учению. Оборудование: учебник, дидактические материалы по алгебре и началам анализа для 11 класса, карточки с разноуровневыми заданиями . . Урок по алгебре и началам анализа в 11 классе Тема: « Производная и первообразная показательной функции» Ход урока Эпиграф: «Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет». Г.Ф. Лейбниц Структура урока I. Вступительное слово учителя. Организационный этап. «Сегодня мы повторим и закрепим знания по данной теме. Урок у нас не совсем обычный. Мы совершим путешествие. А напутствием будут слова эпиграфа, который надо расшифровать, решив устно упражнения (на два варианта). Решайте по порядку. Сразу ищите ответ и соответствующее ему слово». (На доске записаны упражнения для устной работы, а на столах учащихся – карточки для расшифровки эпиграфа). II. Устная работа.
Для расшифровки эпиграфа достаточно выбрать верные ответы и соответствующее им слово.
Учащиеся, расшифровав фразу, записывают ее на лист и сдают учителю. Проверяем работу. Несколько человек зачитывают фразу. I вариант: Кто хочет ограничиться настоящим без знания II вариант: прошлого, тот никогда его не поймет. За правильно расшифрованный эпиграф учащимся начисляется три балла. «Вы знаете, что путешествовать интереснее всего с друзьями. И сейчас вам, ребята, предстоит выбрать друзей, а для этого вы выполните 1 задание из карточки. Всего в карточке 3 задания. Они записаны по возрастающей сложности. Первое – 1 балл, второе – 2 балла, третье – 3 балла». III. Самостоятельная работа (дифференцированная) Карточки для самостоятельной работы
Краткие решения и ответы к самостоятельной работе.
Для самостоятельной работы использованы задания из книги «Задачи по алгебре и началам анализа для 10-11 классов». Саакян С.М. и др. Работа учащимися пишется под копировку. Верхний лист сдают учителю. Верные решения записаны на доске. Учащиеся сверяют своё решение с решением на доске, начисляют себе баллы. Далее происходит пересадка учащихся. Садятся на I ряд: кто получил верный ответ в задании 1) и не получил верного ответа в заданиях 2) и 3). На II ряд садятся те, кто получил верный ответ в задании 2). На III ряд садятся те, кто получил верный ответ в задании 3). Итак, группы сформированы. Но надо знать дорогу, по которой пойдет каждая группа, то есть её рельеф. Известно, что местность, где пролегает дорога, описывается функцией, которую нужно исследовать на монотонность и экстремумы. IV. Работа в парах. Каждой группе предлагается функция, которую нужно исследовать (задания разноуровневые). Задание I группе:  Задание II группе:  Задание III группе:  Затем от каждой группы приглашаются учащиеся для записи решения на доске. В обсуждение решений вовлекаются все учащиеся. Решения и ответы к данному виду работы. I. Функция определена и дифференцируема на R. Найдем ее производную  Решим уравнение   Так как  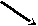, то  - критическая точка.      - + х 0 В точке 0 производная меняет знак с минуса на плюс, поэтому 0 – точка минимума; исходная функция убывает на промежутке (-; 0] и возрастает на промежутке [0; +) .  - минимум функции.II. Функция определена и дифференцируема на R. Найдем ее производную  .Решив уравнение 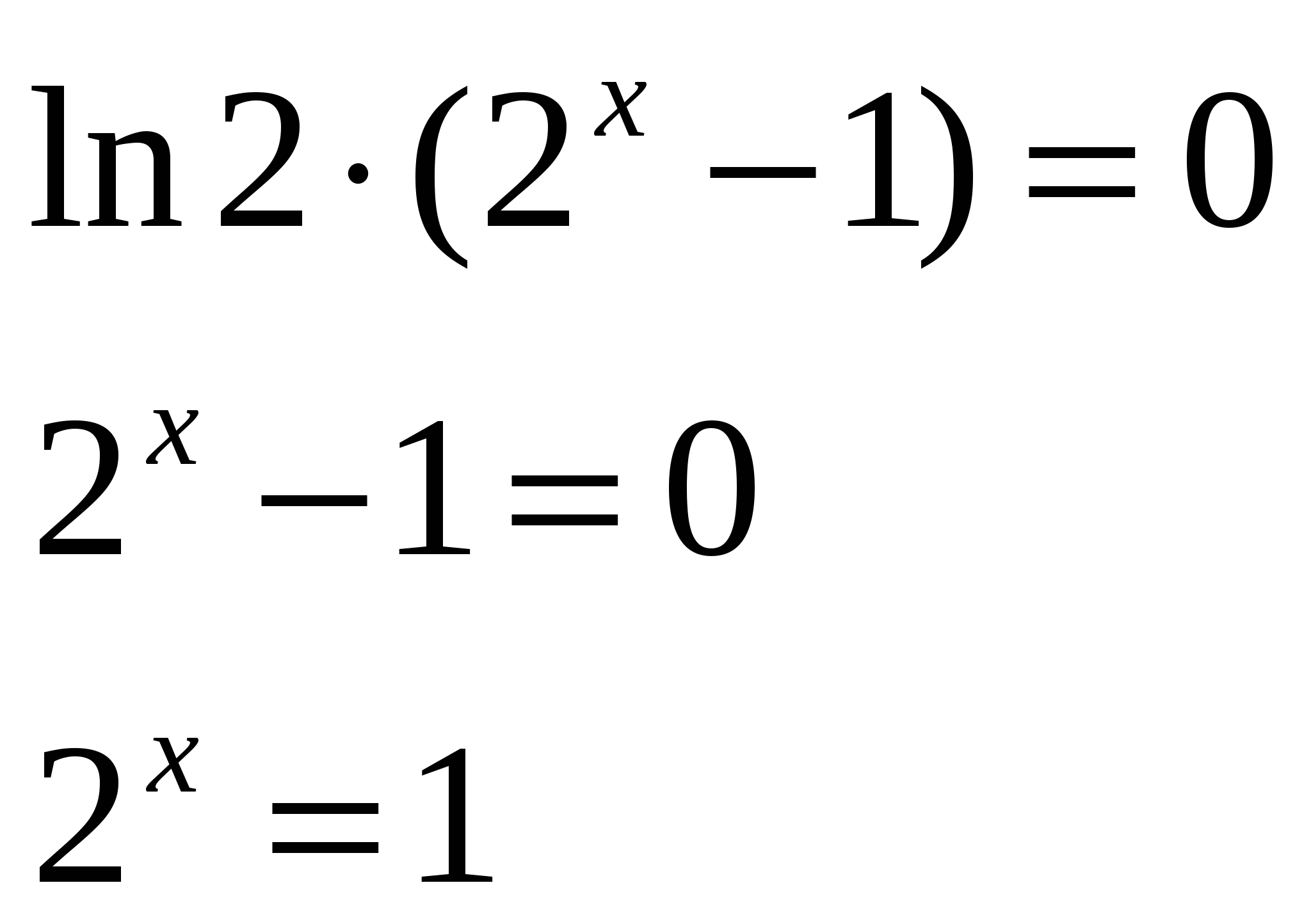, найдем критические точки данной функции. - критическая точка. - + х 0 В точке 0 производная меняет знак с минуса на плюс, поэтому 0 – точка минимума; исходная функция убывает на промежутке (-; 0] и возрастает на промежутке [0; +) .  - минимум функции.III. Третьей группе предлагаем выбрать верный ответ из трёх предложенных. 1 - + min - max )  х    1  - минимум функции - максимум функции- + min max 2) х +  -1  - максимум функции - минимум функции- + - 3 х min max 1 )  - минимум функции - максимум функцииОчевидно, что верный ответ 1) За верное решение учащиеся начисляют себе 1 балл. Итак, наше путешествие продолжается, и мы держим путь в городской парк, где примем участие в конкурсе на создание лучшего проекта клумбы для цветов. V. Работа в группах. Задания группам: создать проект клумбы, то есть изобразить указанные линии на координатной плоскости и вычислить площадь фигуры, ограниченной этими линиями, а затем защитить ваш проект. Работают в группах, могут тихо совещаться, затем 1 человек от группы защищает проект, балл выставляется одинаковый всей группе. Максимальный – 3 балла. Учащиеся других групп принимают участие, задавая вопросы. Клумбы должны иметь форму плоской фигуры, которую можно было бы ограничить линиями: кривыми и прямыми. Учащиеся решают разноуровневые задачи. Задание группам: Вычислите площадь фигуры, ограниченной линиями (ответ округлите до единиц): I группа    II группа    III группа   Решения и ответы: I группа 1) Изобразим данные линии на координатной плоскости и выделим интересующую нас фигуру (см. рис.1в приложении). 2) Фигура АВСD - криволинейная трапеция, поэтому ее площадь находим по формуле площади криволинейной трапеции:  Ответ: 4 II группа 1) Изобразим данные линии на координатной плоскости и выделим интересующую нас фигуру (см. рис.2 в приложении). 2) Фигура АВС не является криволинейной трапецией. Ее площадь найдем так:  .Фигура DАВСМ – криволинейная трапеция, поэтому  Фигура DАСМ – квадрат, поэтому   Ответ: 1 III группа 1) Изобразим данные линии на координатной плоскости и выделим интересующую нас фигуру (см. рис.3 в приложении). 2) Фигура АВС не криволинейная трапеция, но она симметрична относительно оси ОУ  3) Найдем координаты точки С . Абсциссу найдем, решив уравнение:  Таким образом С (1;2). 4) Проведём через точку С прямую  . 5)  Ответ: 1 VI. Подведение итогов. Вот и подходит к концу наше путешествие. Давайте подведём итоги урока. Оцените свою работу на уроке. Выразите своё отношение к уроку. “5” – 10 баллов “4” – 8-9 баллов “3” – 3-7 баллов VII. Домашнее задание. Придумать (или подобрать) и решить две задачи с практическим содержанием на вычисление площади фигуры и на исследование функции на монотонность и экстремумы. Литература: 1. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. / Под редакцией А.Н. Колмогорова.-М.: Просвещение, 2003 год. 2. Дидактические материалы по алгебре и началам анализа для 11 класса:/Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. 3. Задачи по алгебре и началам анализа для 10-11 классов / С.М. Саакян, А.М. Гольдман, Д.В. Денисов. 4. Программы общеобразовательных учреждений по алгебре и началам математического анализа 10-11 классы. / Составитель Бурмистрова Т. А. М. Просвещение, 2009./ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
касательная параллельна прямой 
-
