Контрольная работа Вариант №744089 b найдите значение выражения
 Скачать 172 Kb. Скачать 172 Kb.
|
| Вводная контрольная работа Вариант № 744089 B 1. Найдите значение выражения A 1. Одно из чисел 1) A 2. Какое из чисел больше: 1) B 2. Решите уравнение B 3. Найдите значение 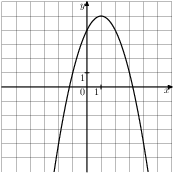 Варианты ответа
B 5. Упростите выражение A 3 . На каком рисунке изображено множество решений неравенства 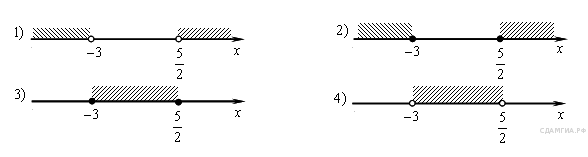 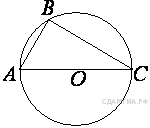 1) 1 2) 2 3) 3 4) 4 B 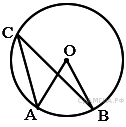 6. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°. Ответ дайте в градусах. 6. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°. Ответ дайте в градусах.B 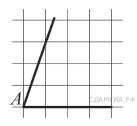 7. Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах). 7. Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).B 8. Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на B 9 . На квадратной сетке изображён угол B 10 . Укажите номера верных утверждений. 1) Через любую точку проходит не менее одной прямой. 2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны. 3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны. A 4. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года.
Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 111 км/ч на участке дороги с максимальной разрешённой скоростью 80 км/ч? 1) 500 рублей 2) 1000 рублей 3) 2000 рублей 4) 5000 рублей B 11. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
Какой вывод о суточном потреблении жиров, белков и углеводов мужчиной можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 150 г жиров, 120 г белков и 611 г углеводов? В ответе укажите номера верных утверждений. 1) Потребление жиров в норме. 2) Потребление белков в норме. 3) Потребление углеводов в норме. B 12. Суточная норма потребления витамина С для взрослого человека составляет 60 мг. Один помидор в среднем содержит 17 мг витамина С. Сколько процентов суточной нормы витамина С получил человек, съевший один помидор? Ответ округлите до целых. B 13 . Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка — 3 км/ч. Какое расстояние (в километрах) будет между ними через 30 минут? B 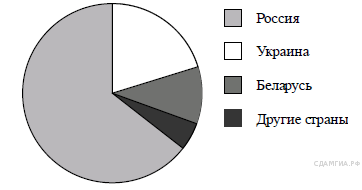 14. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей. Какое из следующих утверждений неверно? 14. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей. Какое из следующих утверждений неверно?1) Пользователей из России больше, чем пользователей из Белоруссии и Украины вместе. 2) Пользователей из Украины больше, чем пользователей Латвии. 3) Примерно две трети общего числа пользователей — из России. 4) Пользователей из Украины больше 3 миллионов. В ответ запишите номер выбранного утверждения. B 16. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C 1. Решите уравнение C 2. Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 4 км/ч, а собственная скорость лодки 6 км/ч? C 4. В прямоугольном треугольнике Вариант № 744143 B 1. Найдите значение выражения A 1. На координатной прямой отмечены числа 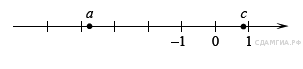 1) A 2. Какое из следующих выражений равно 1) B 2. Решите уравнение B 3. На рисунке изображён график функции 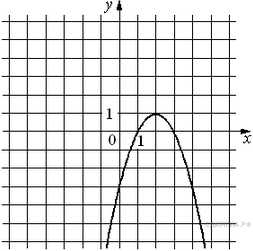
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
B 5. Упростите выражение В ответ запишите полученное число. A 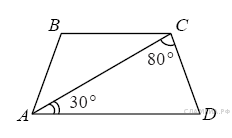 3. Решите неравенство 3. Решите неравенство 1) B 6. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно. B  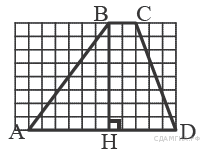 7. Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности. 7. Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.B 8. В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника. B 9. На рисунке изображена трапеция B 10. Какие из следующих утверждений верны? 1) Через любые три точки проходит не более одной окружности. 2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек. 3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются. 4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°. A 4. В таблице даны результаты забега мальчиков 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,5 с.
Укажите номера дорожек, по которым бежали мальчики, получившие зачет. 1) I, IV 2) II, III 3) только III 4) только IV B 11. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
Какой вывод о суточном потреблении жиров, белков и углеводов женщиной можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 55 г жиров, 61 г белков и 255 г углеводов? В ответе укажите номера верных утверждений. 1) Потребление жиров в норме. 2) Потребление белков в норме. 3) Потребление углеводов в норме. B 12. Товар на распродаже уценили на 20%, при этом он стал стоить 520 р. Сколько рублей стоил товар до распродажи? B 13. За сколько часов Земля повернется вокруг своей оси на 120°? B 14. В доме располагаются однокомнатные, двухкомнатные, трёхкомнатные и четырёхкомнатные квартиры. Данные о количестве квартир представлены на круговой диаграмме. Какое утверждение относительно квартир в этом доме неверно, если всего в доме 180 квартир?  1) Больше половины квартир двухкомнатные. 2) Однокомнатных квартир менее четверти. 3) Четверть всех квартир — трёхкомнатные. 4) Однокомнатных, двухкомнатных и трёхкомнатных квартир всего более 165. B 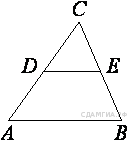 16. Закон Кулона можно записать в виде 16. Закон Кулона можно записать в виде C 1. Решите систему уравнений С2. Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шёл со скоростью, на 1 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку. C 4. В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 9. Найдите площадь треугольника ABC. Вариант № 744206 B 1. Найдите значение выражения A 1. На координатной прямой отмечены числа x, y и z. Какая из разностей z − x, x − y, z − y положительна? 1) z − x 2) x − y 3) z − y 4) ни одна из них A 2. Какому из следующих выражений равна дробь 1) B 2. Решите уравнение B 3. Укажите соответствие между графиками функций и формулами, которые их задают. 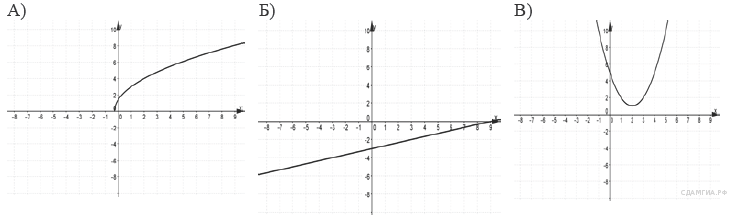 1) Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке В 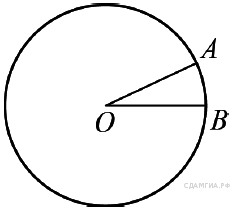 6. Н 6. Н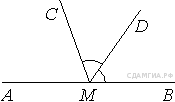 а прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 60°. Найдите угол CMA. Ответ дайте в градусах. а прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 60°. Найдите угол CMA. Ответ дайте в градусах.B 7. На окружности с центром O отмечены точки A и B так, что Д 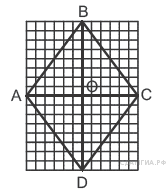 лина меньшей дуги AB равна 63. Найдите длину большей дуги. лина меньшей дуги AB равна 63. Найдите длину большей дуги.B 8. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой. B 9. На рисунке изображен ромб B 10. Укажите номера верных утверждений. 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Треугольник со сторонами 1, 2, 4 существует. 3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат. 4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника. A 4. В таблице приведены нормативы по прыжкам с места для учеников 11 класса.
Какую оценку получит девочка, прыгнувшая на 167 см? 1) «5» 2) «4» 3) «3» 4) «Неудовлетворительно» B 11. На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов в первой половине дня температура превышала 25 °C? 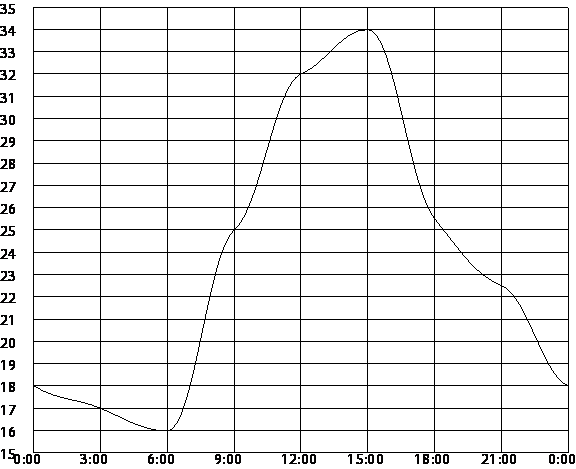 B 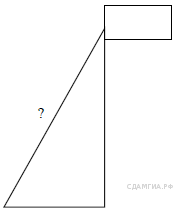 12. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников? 12. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?B 13. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 4,4 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 3,3 м. Найдите длину троса в метрах. B 14. Родительский комитет закупил 20 пазлов для подарков детям на окончание года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Илюше достанется пазл с машиной. B 16. Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 155° по шкале Фаренгейта? Ответ округлите до десятых. C 1. Решите уравнение: C 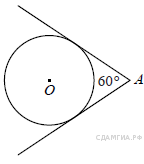 2. Катер прошёл от одной пристани до другой, расстояние между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся обратно через 2. Катер прошёл от одной пристани до другой, расстояние между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся обратно через C 4. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8. Вариант № 744251 B 1. Расположите в порядке убывания числа 0,1327; 0,014; 0,13.
A 1. На координатной прямой отмечено число a. Найдите наименьшее из чисел a2, a3, a4. 1) a2 2) a3 3) a4 4) не хватает данных для ответа A 2. Расположите в порядке возрастания числа: Варианты ответа
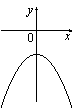
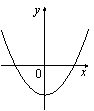
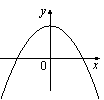
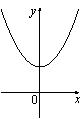
B 2. Уравнение B 3. На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и знаками коэффициентов a и c. ГРАФИКИ
ЗНАКИ КОЭФФИЦИЕНТОВ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
B 5. Упростите выражение A 3. Р 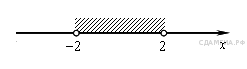 ешение какого из данных неравенств изображено на рисунке? ешение какого из данных неравенств изображено на рисунке?1 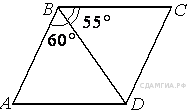 ) ) 2) B 6. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма. B 7. Н 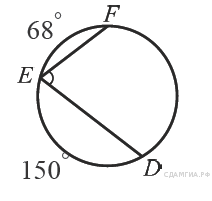 айдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно. айдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.B 8. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на B 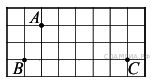 9. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах. 9. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.B 10. Какие из следующих утверждений верны? 1) Около любого правильного многоугольника можно описать не более одной окружности. 2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника. 3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей. 4) Около любого ромба можно описать окружность. A 4. Бизнесмен Петров выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.
Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят бизнесмену Петрову. 1) 038А 2) 020У 3) 016А 4) 116С B 11. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
Какой вывод о суточном потреблении жиров, белков и углеводов 8-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 84 г жиров, 65 г белков и 455 г углеводов? В ответе укажите номера верных утверждений. 1) Потребление жиров в норме. 2) Потребление белков в норме. 3 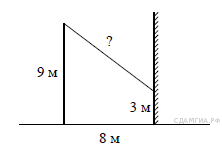 ) Потребление углеводов в норме. ) Потребление углеводов в норме.B 12. В городе 190 000 жителей, причем 29% – это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч. B 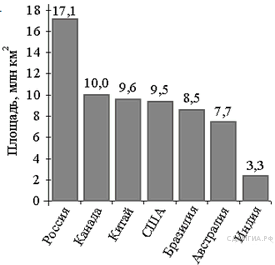 13. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода. 13. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.B 14. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира. Какое из следующих утверждений неверно? 1) По площади территории Австралия занимает шестое место в мире. 2) Площадь территории Бразилии составляет 7,7 млн км2. 3) Площадь Индии меньше площади Китая. 4) Площадь Канады меньше площади России на 7,1 млн км2. B 16. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта ( C 1. Решите неравенство C 2. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба? C 4. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||