Наименование продукта
 Скачать 39.82 Kb. Скачать 39.82 Kb.
|
| Часть 1 Ответом на задания В1–В14 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке. Единицы измерений писать не нужно. В1 Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 60 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды? В2 На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите разность между среднемесячными температурами июля и ноября. Ответ дайте в градусах Цельсия. 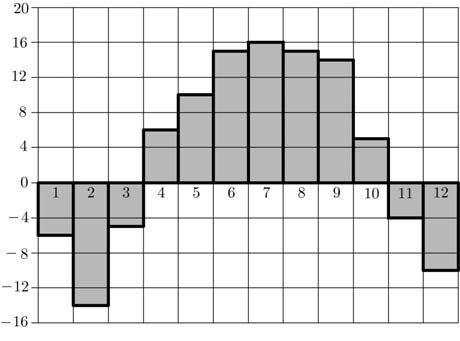 В3 Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 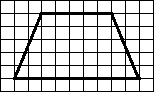 В4 В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трех городах России (по данным на начало 2010 года).
В каком из этих городов была самой низкой стоимость набора продуктов: 3 л молока, 1 кг говядины, 1 л подсолнечного масла? В ответе запишите эту стоимость (в рублях). В5 Найдите корень уравнения 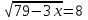 . .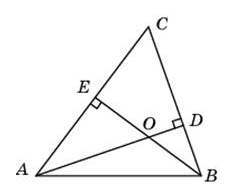 В6 В треугольнике АВС угол А равен 41°, угол В равен 74°, высоты AD и BE пересекаются в точке О. Найдите угол АОВ. Ответ дайте в градусах. В7 Найдите 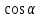 , если , если 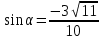 и α и α 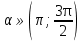 . .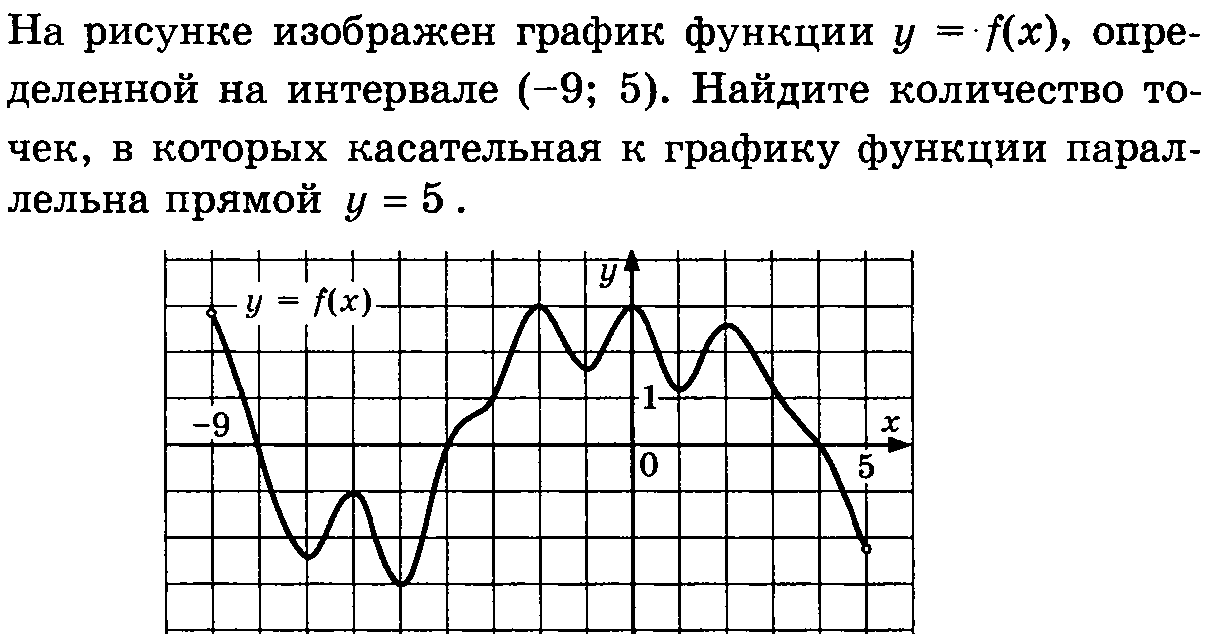 В8 На рисунке изображен график функции y = f(x), определенной на интервале (–9; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 5. 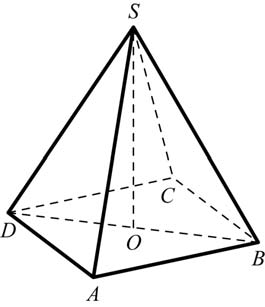 В9 В правильной четырёхугольной пирамиде SABCD точка O – центр основания, SO = 24, BD = 36. Найдите боковое ребро SA. В10 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. В11 Найдите боковое ребро правильной четырёхугольной призмы, если сторона её основания равна 2, а площадь поверхности равна 104. В12 Высота над землёй подброшенного вверх мяча меняется по закону 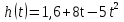 , где , где 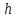 - высота в метрах, - высота в метрах, 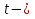 время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находится на высоте не менее трех метров? время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находится на высоте не менее трех метров?В13 Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч. В14 Найдите точку максимума функции 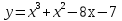 . .Часть 2 Для записи решений и ответов на задания C1–C4 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ. С1 Решите уравнение 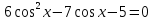 . Укажите корни, принадлежащие отрезку [−π; 2π]. . Укажите корни, принадлежащие отрезку [−π; 2π].С2 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 4, найдите расстояние от точки A до прямой B1C1. С3 Решите неравенство 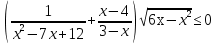 . .С4 Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 14, а отношение катетов треугольника равно 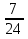 . . |