Пример нестандартного решения некоторой текстовой задачи школьного курса математики
 Скачать 24.04 Kb.
|
Пример нестандартного решения некоторой текстовой задачи школьного курса математики.Некоторые текстовые задачи при решении у учащихся вызывают затруднения. На примере одной задачи я хочу показать нестандартное решение, которое может быть применено и к другим задачам, например, при решении задач на совместно произведённую работу. Задача Л. Н. Толстого) Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру ещё остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели? Решение. Данная задача эквивалентна следующей. Имеются два резервуара, объём одного из них вдвое больше другого. Резервуары могут заполняться жидкостью от источника с пропускной способностью G через систему трубопроводов одинакового диаметра с кранами K1 и K2 . 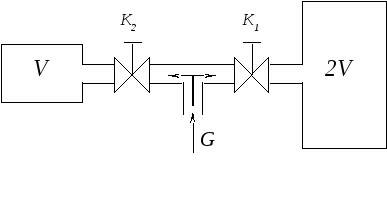 Полдня заполнялся большой резервуар (кран K2 был закрыт) и в результате в него поступило количество жидкости, равное  . После этого был открыт кран K2 и оставшиеся полдня оба резервуара заполнялись одновременно, причём больший резервуар оказался заполненным. Поэтому, учитывая разветвление потока, за оставшиеся полдня в каждый резервуар поступило количество жидкости, равное  . Так как при таком режиме работы больший резервуар оказался заполненным, то в результате получаем следующее уравнение:  G=2V (1)На следующий день производительность источника уменьшили в k раз так, чтобы оставшаяся часть объёма малого резервуара заполнялась полный день. В результате получаем следующее уравнение: + =V (2)Уравнения (1) и (2) позволяют установить, во сколько раз была уменьшена производительность источника. Действительно, поделив уравнение (1) на уравнение (2), получим: 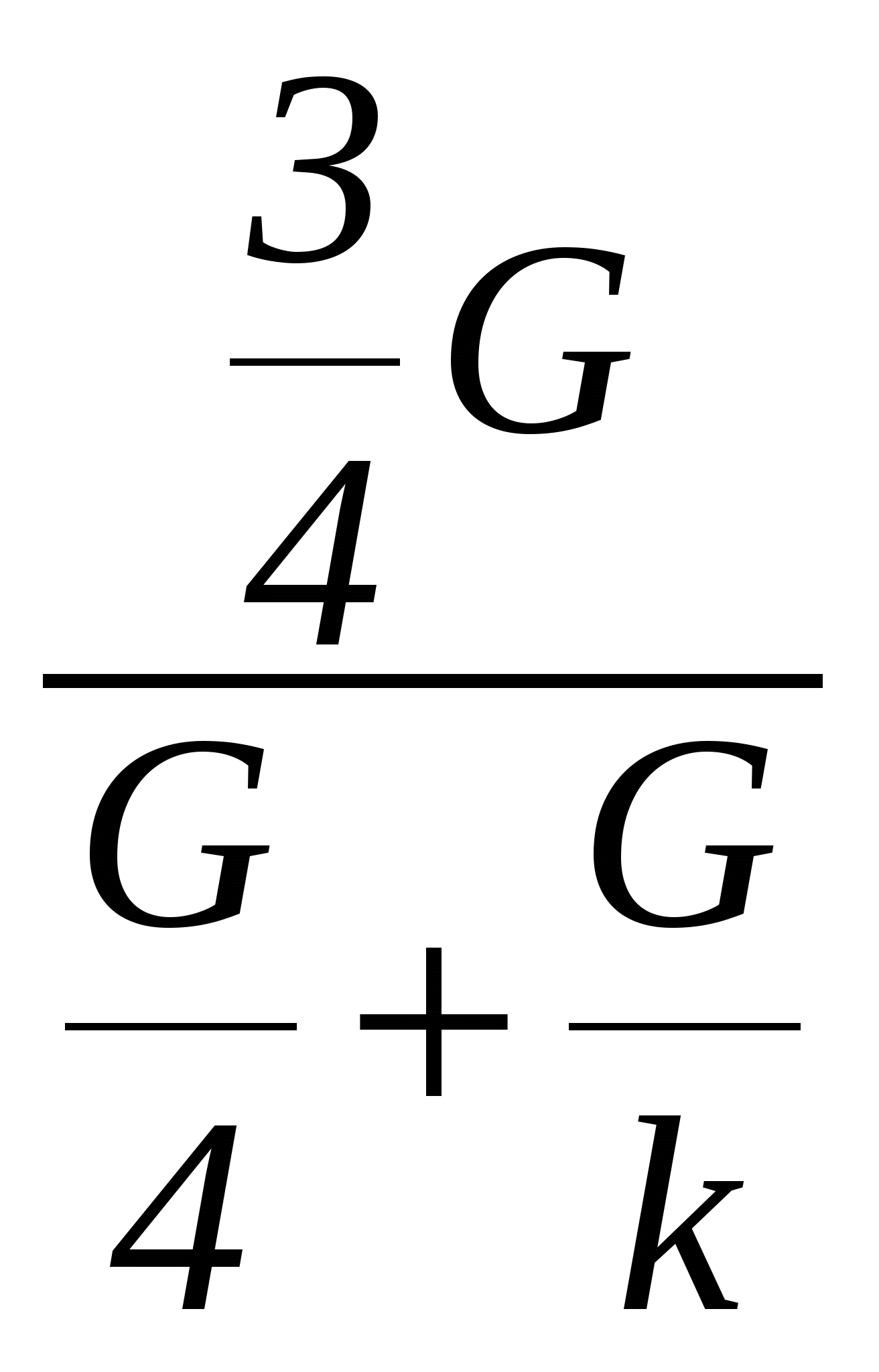 =2 k=8.Легко убедиться, что значение k=8 в исходной задаче как раз соответствует числу косцов в артели. Для этого рассмотрим решение этой задачи по традиционной схеме. Пусть x – число косцов артели, y – размер участка, скашиваемого одним косцом за один день. Заметим, что y представляет вспомогательное переменное, которое вводится для облегчения решения задачи, и в итоге сокращается. Далее выразим через x и y площади большого и малого луга. Площадь большого луга равняется  площадь малого луга  . Большой луг по условию больше малого в 2 раза  или  . После сокращения на y получим: x=8. Ответ: 8 косцов.Данный метод отличается большей наглядностью, что, как показал опыт, обеспечивает лучшее восприятие данного материала у детей, по сравнению с традиционными методиками; дети с удивлением обнаруживают, что, казалось бы, различные ситуации описываются одинаковыми математическими моделями и в принципе решение одной задачи подменяется решением другой более наглядной. Подробнее с данным методом решения задач можно познакомиться в работе Игошин В.И., Серебрякова И.В., Фирстов В.Е. «Идеи изоморфизма и её интерпретация при решении текстовых задач в школьном курсе алгебры» (Сборник «Актуальные вопросы региональной педагогики» Саратов.:Издательство СГУ, 2005 год,стр.32-43). https://pedsovet.org/index.php?option=com_mtree&task=viewlink&link_id=74396&mosmsg=%D1%EF%E0%F1%E8%E1%EE%2C+%E4%EE%E1%E0%E2%EB%E5%ED%ED%E0%FF+%E2%E0%EC%E8+%E8%ED%F4%EE%F0%EC%E0%F6%E8%FF+%EE%EF%F3%E1%EB%E8%EA%EE%E2%E0%ED%E0. |