Контрольная работа по геометрии для 10-го класса по материалам открытого банка егэ
 Скачать 39.48 Kb.
|
| КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ ДЛЯ 10-го КЛАССА ПО МАТЕРИАЛАМ ОТКРЫТОГО БАНКА ЕГЭ 1. В прямоугольном параллелепипеде ABCDA1B1C1D1 D1В = 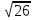 , ВВ1 = 3, А1D1 = 4. Найдите длину ребра А1В1.2. В правильной четырехугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 10, BD = 48. Найдите боковое ребро SA. 3. Стороны основания правильной четырехугольной пирамиды равны 42, боковые ребра равны 75. Найдите площадь поверхности этой пирамиды. 4. В правильной треугольной пирамиде SABC М – середина ребра АВ, S – вершина, ВС = 4, SМ = 3. Найдите площадь боковой поверхности пирамиды. 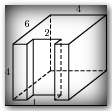 5. Площадь поверхности куба равна 200. Найдите его диагональ. 6. Если каждое ребро куба увеличить на 9, то его площадь поверхности увеличится на 594. Найти ребро куба. 7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 32 и 42. Площадь поверхности параллелепипеда равна 6240. Найдите его диагональ. 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 40, и боковым ребром, равным 55. 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 1. В прямоугольном параллелепипеде ABCDA1B1C1D1 С1А = 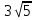 , СС1 = 2, А1D1 = 5. Найдите длину ребра CD.2. В правильной четырехугольной пирамиде SABCD точка О – центр основания, S – вершина, SD = 13, BD = 10. Найдите длину отрезка SО. 3. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. 4. В правильной треугольной пирамиде SABC К – середина ребра СВ, S – вершина, ВА = 6, а площадь боковой поверхности равна 63. Найдите длину отрезка SК. 5. Площадь поверхности куба равна 1568. Найдите его диагональ. 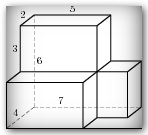 6. Если каждое ребро куба увеличить на 2, то его площадь поверхности увеличится на 192. Найти ребро куба. 7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 12. Площадь поверхности параллелепипеда равна 192. Найдите его диагональ. 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 5 и 12, и боковым ребром, равным 17. 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 1. В прямоугольном параллелепипеде ABCDA1B1C1D1 АС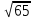1 =  , DD1 = 5, В1С1 = 6. Найдите длину ребра D1C1.2. В правильной четырехугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 7, АС = 48. Найдите боковое ребро SВ. 3. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности этой пирамиды. 4. В правильной треугольной пирамиде SABC Р – середина ребра ВС, S – вершина, АВ = 7, SР = 16. Найдите площадь боковой поверхности пирамиды. 5. Площадь поверхности куба равна 242. Найдите его диагональ. 6. Если каждое ребро куба увеличить на 2, то его площадь поверхности увеличится на 144. Найти ребро куба. 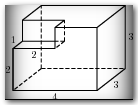 7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 12. Площадь поверхности параллелепипеда равна 576. Найдите его диагональ. 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 5 и 12, и боковым ребром, равным 16. 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |