Решение задачи№1(№2-4 решаются аналогично)
 Скачать 26.69 Kb.
|
 Задачи на совместную работу с решением(ЕГЭ №13)1.Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше? 2.Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше? 3.На изготовление 391 детали первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 460 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий? 4. На изготовление 16 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 40 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий? 5.Двое рабочих, работая вместе, могут выполнить работу за 15 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 2 дня выполняет такую же часть работы, какую второй — за 3 дня 6Двое рабочих, работая вместе, могут выполнить работу за 15 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 2 дня выполняет такую же часть работы, какую второй — за 3 дня? 7Двое рабочих, работая вместе, могут выполнить работу за 20 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 3 дня выполняет такую же часть работы, какую второй — за 4 дня? Решение задачи№1(№2-4 решаются аналогично) Работа это количество деталей. В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем её за х (деталей в час). Тогда производительность первого рабочего будет равна х+1 (он делает на одну деталь в час больше). Поскольку t=A/p, то время работы первого рабочего будет равно: 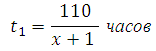 время работы второго равно: 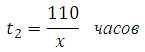 Занесём данные в таблицу: 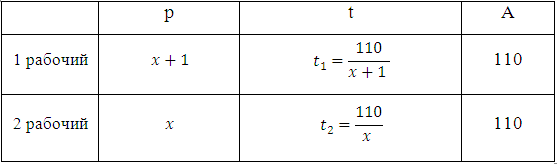 Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй. Значит 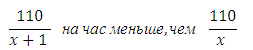 Можем записать: 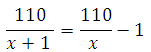 Уравнение сводится к квадратному: 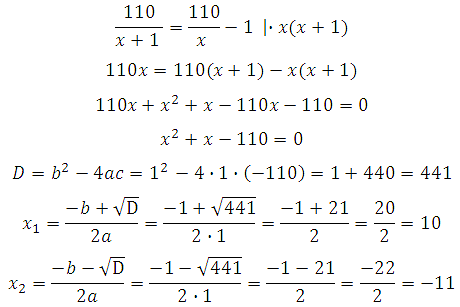 Очевидно, что производительность рабочего не может быть отрицательной величиной. Ответ: 10 Решение задачи№5(№6,7 аналогично) Пусть x - число дней, за которое первый рабочий выполняет работу, работая отдельно, а y - число дней, за которое второй рабочий выполнит работу, работая отдельно. Тогда за один день первый выполнит  часть работы, второй -  часть работы. По условию, работая вместе, за день они выполняют  часть работы, т.е.  Также из условия известно, что первый рабочий за 2 дня выполняет такую же часть работы, какую второй за 3 дня, т.е. 2  = 3   Подставим последнее выражение в уравнение (1):       Ответ: 20 |