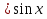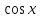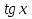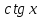обучение на тренера тренажерного зала Курсы для тренеров по фитнесу. Курсы инструктора тренажерного зала. О нас.
Конспект урока Игра «Математический аукцион»
 Скачать 40.83 Kb. Скачать 40.83 Kb.
|
| Автор игры Князькина Татьяна Викторовна, учитель математики МБОУ «СОШ №143» г. Красноярска Конспект урока Игра «Математический аукцион» по программе углубленного изучения математики в 9 классе автора Виленкин Н. Я. Математический аукцион – это урок – соревнование, который заслуженно можно назвать азартной игрой. Его можно проводить как в форме личного состязания, так и в форме командного. На данном уроке учащиеся работали в группах. Тема урока зашифрована в анаграмме «ОРИМЯТОРИНЕГТ», которую учащиеся определяют без труда– «Тригонометрия», т. е. тригонометрические функции, их свойства, тригонометрические преобразования. На уроке 4 команды. В начале урока учитель на правах аукциониста объявляет правила игры. Суть их в следующем: Каждая команда получает одинаковое количество денежных единиц (они могут быть названы по разному: «кошки», «мышки», «слоники» и т. д.) Каждой команде выдается список 9 заданий, каждое из которых – это лот №1, лот №2,и т. д. Лот №9 – призовой, за который взявшая его команда получает весь банк аукциона. Понятно, что это наиболее сложное задание. Каждый лот имеет первоначальную стоимость, в зависимости от сложности задания. Во время торгов цена может повышаться. Если задание не выполнено, то внесенная в банк денежная сумма возвращается обратно команде. Побеждает та команда, которая вносит в банк аукциона наибольшее количество денежных единиц, тем самым оставляя на «руках» наименьшую сумму. Во время озвучивания решенных заданий каждый участник аукциона имеет право на помощь в виде подсказки. Если помощь осуществляет собственная команда—штраф из банка аукциона. Если подсказку делает команда соперников – штраф из фонда соперников в фонд тех, кому помогают. После озвучивания всех лотов каждой команде необходимо подсчитать оставшиеся денежные единицы. Во время розыгрыша призового лота торг не уместен. Когда команды изучают список восьми заданий, они оценивают свои интеллектуальные возможности. Можно взять лот «подешевле» и справиться с заданием, но соперники в таком случае могут внести в банк аукциона большую сумму денежных единиц, выкупив после торгов «дорогое» задание! Можно претендовать на «дорогой» лот, но с заданием не справиться. Риск! После продажи лотов время на решение для всех команд одинаковое. Затем представитель команды озвучивает решение у доски. В это время все ученики внимательно следят за ходом решения и при малейшей заминке вносят дополнения или подсказки. Азарт игры! Итак, торги прошли, все лоты озвучены, команды считают оставшиеся денежные единицы. Определяется команда, победившая в аукционе. Наступило время призового девятого лота. Вероятнее всего, что его выкупит команда, уверенная в своих математических способностях. Чтобы не задеть самолюбие остальных, им можно дать дополнительный шанс в виде сложных заданий. Справились – хорошо! Прослушав версию решения призового лота, подводим итог. Ученики сами проставляют оценки в рабочей карте урока:
На уроке – игре «плохих» оценок не бывает, так как все ученики включены в работу. Последнее слово за учителем – аукционистом. Педагог должен очень умело подвести итог, чтобы не ущемить самолюбие проигравших, так как азарт повышает математический интерес у всех учащихся, независимо от уровня подготовки. Приложение к уроку. Лот №1 (20 ден. ед.) Задание. Дать определение функции и перечислить её свойства:
Лот №2 (50 ден. ед.) Задание. Решить неравенство: x2 +x(cos2+cos3)+cos2cos3<0 указать какое – нибудь рациональное число, ему не удовлетворяющее. Лот №3 (100 ден. ед.) Задание. Числа sin5; 0,5cos25;sin55 составляют арифметическую прогрессию. Докажите это утверждение. Лот №4 (80 ден. ед.) Задание. Вычислить: tg4 a+ctg4 a, если tg a – ctga=b Лот №5 (200 ден. ед.) Задание. Зная, что А, В, С – внутренние углы некоторого треугольника, докажите справедливость равенства: sin4A+ sin4B+ sin4C=-4 sin2A· sin2B· sin2C Лот №6 (180 ден. ед.) Задание. Докажите справедливость равенства: sin10· sin30· sin50· sin70= 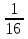 Лот №7 (120 ден. ед.) Задание. Вычислить: 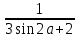 , если tga=0,1 , если tga=0,1Лот №8 (150 ден. ед.) Задание. Упростить выражение: 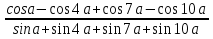 Лот №9 (призовой) Задание. Найти наименьшее целое значение выражения: 18cos2x+24sin2 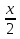 +4,59 +4,59Подводя итог, хочу сказать, что урок – игра уникален по своей сути, так как дает положительный заряд не только ученикам, но и учителю. Поверьте, азарт в обучении и учении – огромный стимул в двуедином учебном процессе. В игре выражают себя все принципы дидактических технологий: принцип свободы выбора, принцип активности, принцип деятельности, принцип обратной связи. Играйте на уроках, так как «вся наша жизнь – игра!» |