Мбоу «сош №143» г. Красноярска Метапредметный проект «Криптография: алгоритм rsa»
 Скачать 422.14 Kb.
|
2.3. Расширенный алгоритм ЕвклидаУ алгоритма Эвклида есть еще один вариант. Достоинство нового варианта в том, что наибольший общий делитель — лишь часть выходных данных. Пусть a и b — натуральные числа, а r — их наибольший общий делитель. Расширенный алгоритм Эвклида подсчитывает не только r, но и два целых числа c и d таких, что r =d *a+c*b. Отметим, что если d оказывается положительным, то c — отрицательное, и наоборот. Лучше всего вычислять эти числа, добавив некоторые инструкции в обычный алгоритм Эвклида так, чтобы r, c и d подсчитывались одновременно. Именно поэтому новая процедура называется расширенным алгоритмом Эвклида. Формулы для остатков ri из алгоритма Евклида могут быть переписаны следующим образом: r1=a -bq1 r2=b - r1q2 =b-q2 (a –bq1) =b(1+ q1q2)-aq2 … rn =d *a+c*b . Тогда НОД(a,b)=rn =d *a+c*b, где d и с – целые числа. Это представление наибольшего общего делителя называется соотношением Безу или линейным представлением НОД, а числа d и c — коэффициентами Безу. Пример 2. Выписать соотношение Безу для чисел 1840 и 135 с помощью расширенного алгоритма Евклида. Воспользуемся таблицей 1. НОД(1840,135)=5=35-15*2=5-2*(50-35)=35-2*50+2*35=3*35-2*50=3*(85-50)-2*50=3*85- -3*50-2*50=3*85-5*50=3*85-5*(135-85)=3*85-5*135+5*85=8*85-5*135=8*(1840-13*135)-5*135=8*1840-13*8*135-5*135=8*1840-109*135=8*a+(-109)*b Соотношение Безу или линейное представление НОД для данного примера НОД(a,b)=rn =d *a+c*b=8*a+(-109)*b. 2.4. Функция Эйлера Мне также понадобится функция, которая была названа в честь великого математика Леонарда Эйлера, который впервые использовал ее в своих работах по теории чисел. Функция Эйлера (m), где m — натуральное число, равна количеству натуральных чисел, не больших m и взаимно простых с ним. Пример 3. Пусть m=15. Выпишем все натуральные числа меньшие либо равные 15 и выделим жирным шрифтом взаимно простые с 15: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15. Нетрудно посчитать, что (15)=8. Выпишем некоторые свойства функции Эйлера.
Например, 15 можно представить как произведение взаимно простых чисел 3 и 5, тогда по свойству 2 (15)= (5*3)= (5)*(3). Так как 3 и 5 простые числа, то воспользуемся свойством 1 и получим (15)= (5*3)= (5)* (3)=(5-1)(3-1)=4*2=8. Таким образом, из свойств 1 и 2 вытекает свойство 3, которые мы будем использовать в алгоритме RSA:
2.5. Методы поиска простых чисел Всякий, кто изучает простые числа, бывает очарован и одновременно ощущает собственное бессилие. Определение простых чисел так просто и очевидно; найти очередное простое число так легко; разложение на простые сомножители – такое естественное действие. Почему же простые числа столь упорно сопротивляются нашим попыткам постичь порядок и закономерности их расположения? Может быть, в них вообще нет порядка, или же мы так слепы, что не видим его? Ч. Узерелл «Этюды для программистов». Ни одному другому разделу теории чисел не свойственно столько загадочности и изящества, как разделу, занимающемуся изучением простых чисел — непокорных упрямцев, упорно не желающих делиться ни на какое целое число, кроме единицы и самих себя. В теории чисел много проблем, формулировка которых достаточна проста, но решение не поддавалось или не поддаётся до сих пор многим поколениям математиков. Значительная часть таких проблем связана с распределением простых чисел в натуральном ряду. Некоторые задачи, относящиеся к теории распределения простых чисел, формулируются настолько просто, что понять их может и ребенок. Тем не менее они настолько глубоки и далеки от своего решения, что многие математики считают их вообще неразрешимыми. В разные периоды человеческой истории многие выдающиеся математические умы напрягались в поиске ответа на простой вопрос: как часто встречаются простые числа в натуральном ряду? Конкретнее: сколько существует простых чисел, меньших заданного натурального числа n ? Вопрос, казалось бы, простой и понятный, но точного ответа на него до сих пор не знает никто. Развитие математической мысли показало, что задача точного вычисления функции (n) - количества простых чисел, не превосходящих n, является чрезвычайно трудной. Но разгадка тайн природы является благородным и увлекательным занятием, поэтому изучение с разных сторон функции (n) продолжается во всем математическом мире. Большие заслуги в области изучения простых чисел принадлежат русским математикам.
7 = 2 + 2 + 3, 9 = 3 + 3 + 3, 15 = 3 + 5 + 7 = 5 + 5 + 5 . Сама проблема получения простых чисел занимает ключевое место в математике, на ней основаны некоторые криптографические алгоритмы, например RSA. 2.5.1. Решето Эратосфена Очевидно, что любое простое число, не равное 2, является нечетным. Существуют признаки делимости целых чисел на различные простые числа, например, чтобы число делилось на 3 и 9 достаточно, чтобы сумма его цифр делилась на 3 и 9 соответственно. Чтобы число делилось на 5, достаточно, что его последняя цифра была 0 или 5.
Рис. 6. Решето Эратосфена Такие частные признаки делимости можно использовать, если нужно уменьшить множество кандидатов проверки на простоту или отсечь заведомо составные числа. Альтернативным способом получения простых чисел является решето Эратосфена, приписываемое древнегреческому ученому Эратосфену Киренскому, жившему примерно в 276 - 194 г. до н.э. Так как во времена Эратосфена писали на восковых табличках и не вычеркивали, а "выкалывали" цифры, то табличка после описанного процесса напоминала решето. Поэтому метод Эратосфена для нахождения простых чисел получил название "решето Эратосфена". Решето Эратосфена — алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому. Алгоритм Эратосфена для нахождения всех простых чисел не больше заданного числа n.
Таким образом, для нахождения множества простых до заранее выбранной верхней границы n мы сначала вычеркиваем все четные числа кроме 2, затем выписываем последовательность всех нечетных чисел от 3 до n. Затем выбираем первое число в списке, т.е. тройку, и оставляя его в списке, вычеркиваем все кратные 3, начиная с 6. Потом переходим ко второму числу списка (пятерке) и вычеркиваем его кратные, оставив саму пятерку и т.д., пока не дойдем до конца списка. В оставшемся списке будут только простые числа. Мартин Гарднер [7] предложил следующую «конструкцию» решета Эратосфена. Выпишем все целые числа от 1 до 100 в виде прямоугольной таблицы, изображенной на рис. 6. Вычеркнем все числа, кратные 2, за исключением самой двойки, проведя вертикальные черты во втором, четвертом и шестом столбцах. Вычеркнем все числа, кратные 3 (сама тройка остается), проведя вертикальную черту в третьем столбце. Следующее за 3 невычеркнутое число равно 5. Чтобы вычеркнуть числа, кратные 5, проведем диагонали, идущие вниз и влево. Оставшиеся в таблице числа, кратные 7, вычеркнем, проведя диагонали с наклоном вправо и вниз. Числа 8, 9 и 10 — составные, их кратные уже были вычеркнуты раньше. Наша работа по составлению списка простых чисел, не превосходящих числа 100, на этом заканчивается. Итак, все числа, кроме 26, не закрашенных, просеялись сквозь решето. Осталось лишь 26 простых чисел. Математики предпочитают говорить, что осталось лишь 25 первых простых чисел, поскольку многие важные теоремы формируются проще, если 1 не считать простым числом. Решето Эратосфена работает как своего рода вычислительная машина. И, значит, вот что изобрел великий грек: он изобрел счетную машину. Простые числа располагаются на числовом ряду весьма причудливым образом, но, создав Решето Эратосфена достаточно большого размера, мы отсеем (построим) их ВСЕ без исключения. Все они окажутся в дырках совершенно правильного геометрически Решета! 2.5.2. Скатерть Улама В зависимости от расположения целых чисел простые числа могут образовывать тот или иной узор. Однажды математику Станиславу М. Уламу пришлось присутствовать на одном очень длинном и очень скучном, по его словам, докладе. Чтобы как-то развлечься, он начертил на листке бумаги вертикальные и горизонтальные линии и хотел было заняться составлением шахматных этюдов, но потом передумал и начал нумеровать пересечения, поставив в центре 1 и двигаясь по спирали против часовой стрелки. Без всякой задней мысли он обводил все простые числа кружками. Вскоре, к его удивлению, кружки с поразительным упорством стали выстраиваться вдоль прямых. На рисунке показано, как выглядела спираль. Это заинтересовало Улама, и позже он вместе с Майроном Л. Стейном и Марком Б. Уэллсом продолжил это исследование на ЭВМ MANIAC Лос-Аламосской лаборатории, использовав магнитную ленту, на которой были записаны 90 млн простых чисел. Скатерть Улама представляет из себя спираль чисел натурального ряда, на которой отмечены клетки, соответствующие простым числам. 2.5.3. Простые числа Мерсена Числа Мерсенна - это числа, преставимые в виде 2n-1. Особый интерес представляют простые числа Мерсена, которые получаются при n=2, 3, 5, 7, 13, 17, 19, 41, 47, 61, 89, 107, 127, ... Эта последовательность начинается так: 3, 7, 31, 127, 2047, 8191, 131071, 524287, 8388607, 536870911, 2147483647 Наибольшим известным простым числом по состоянию на февраль 2011 года является 243112609 − 1. Оно содержит 12 978 189 десятичных цифр и является простым числом Мерсенна (M43112609). Его нашли 23 августа 2008 года на математическом факультете университета UCLA в рамках проекта по распределённому поиску простых чисел Мерсенна GIMPS. Это же число является наибольшим среди всех известных простых чисел. На сегодняшний день неизвестно: конечно ли число простых чисел Мерсена. 2.5.4. Простые числа Ферма Числа вида 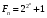 впервые начал изучать Пьер Ферма, поэтому эти числа называются числами Ферма. Он высказал гипотезу, что все эти числа являются простыми, но не смог ни доказать, ни опровергнуть это утверждение. Первые 5 чисел Ферма действительно являются простыми: F0 = 3, F1 = 5, F2 = 17, F3 = 257, F4 = 65537.Гипотеза Ферма о простоте чисел Fn была отвергнута в 1732 г. другим выдающимся математиком Леонардом Эйлером (1707-1783) , который нашел разложение шестого числа Ферма: + 1 = 4 294967 297 = 641 6 700 417 |