| Https://vremya-stroiki.net https://vremya-stroiki.net рабочие перчатки хб: хлопковые перчатки. vremya-stroiki.net |
Методические рекомендации по решению задач для подготовки к огэ и егэ. Вероятность Обращение к выпускникам
 Скачать 157.61 Kb. Скачать 157.61 Kb.
|
                                              Обращение к выпускникам Обращение к выпускникамПри самостоятельной подготовке к ЕГЭ и ОГЭ рекомендую придерживаться изложенного в данной работе системы изложения. В работе проанализированы задания по теории вероятности последних лет и сформированы в цикл, где темы изложены в некоторой последовательности. Это позволит Вам привести в систему знания и умения по решению задач о вероятностях событий. Тематическое планирование занятий по теории вероятности (12 час)
Лекция 1. Определение события. Случайные события. Достоверные и невозможные случайные события. Человека окружает мир событий. Мы часто замечаем такой факт: одни события при реализации данного комплекса условий непременно происходят, другие же могут произойти, а могут и не произойти. Рассмотрим некоторую группу таких событий: Табл. 1
Про события А1 и А5 мы говорим, что они произойдут закономерно., а про события А2, А3, А4 – что они могут произойти, но могло быть и иначе. События А2, А3, А4 позволяют говорить о так называемых случайных событиях. Определение: Случайным событием называется такой исход наблюдения или эксперимента, который при реализации испытания может произойти, а может и не произойти. Обычно случайные события обозначают заглавными латинскими буквами. Например, А, В, С,D и т.д. Подбрасываем монету. Появился, для определенности, герб. А ведь могла появиться цифра. То, что появился герб – случайное событие. Охотник стрелял в волка. Попал. Но мог и не попасть ( произошла осечка, дрогнула рука или еще что – то). Попадание -= случайное событие. На прогулке Аюр встретил трех своих друзей. Конечно, это дело случая: он мог и не встретить их или встретить одного, или встретить двух друзей. Встреча – случайное событие. Определение: Невозможное событие – это когда среди всех возможных элементарных событий при реализации испытания нет ни одного элементарного события, благоприятствующего случайному событию. Определение: Достоверное событие – это когда все возможные элементарные события при реализации испытания благоприятствуют случайному событию Рассмотрим следующий пример: Заданы числа 1, 2, 3. Составим из этих чисел всевозможные трехзначные числа: «к=123», «к=213», «к=312», «к=231», «к=132», «к=321». Пусть событие А={к<123} и B={k≥123}. Тогда говорят, что событие А –невозможное событие, событие В – достоверное событие. Рассмотрим следующий пример: Подбрасываем симметрическую монету. Возможны следующие исходы – «орел» и «решка». Такие события, как событие «орел» и событие «решка» будем в дальнейшем называть элементарными событиями или просто событиями. Упражнение 1. Какие из следующих событий достоверные: А = «два попадания при трех выстрелах» В= « размен рубля семью монетами» С= «наугад выбранное трехзначное число не больше 1000» D= «наугад выбранное число, составленное из цифр 1, 2, 3 без повторений, меньше 400» Решение: О событии А нельзя точно сказать, как достоверное оно или невозможное событие. События В, C,D являются достоверными. Реши самостоятельно Упражнение 2. Какие из следующих событий невозможные: А = «опоздание некоторых учащихся в субботние дни» В= « появление 17 очков при бросании 3 игральных кубиков» С= «появление слова «мама» при случайном наборе букв а, а, м, м» D= «появление составленного из цифр 1, 2, 3, 7, 8 и кратного 9 числа при случайном однократном наборе указанных цифр» Е= «появление составленного из цифр 1, 2, 3, 7, 8 и кратного 3 числа при произвольном однократном наборе указанных цифр». Ответ: D Упражнение3. Какие из следующих событий невозможные: А = «выплата 10 рублей четырьмя купюрами» В= « появление 3 лайнеров над аэропортом» С= «попадание в мишень при 3 выстрелах» Е= «появление в окошке счетчика трехзначного числа, составленного из цифр 1, 2, 3 и кратного 5». Ответ: А- достоверное, Е – невозможное событие. Лекция 2. Классическое определение вероятности события Замечание: 1. Классическое определение вероятности применяется там, где реальные опыты проводить не планируется. 2. Равновозможными элементарными событиями будем считать такие события, любое из которых по отношению к другим событиям не обладает никаким преимуществом появляться чаще другого при многократных испытаниях, проводимых в одинаковых условиях. При бросании игрального кубика возможны события: Табл. 2
В таблице 2 рассмотрены случайные события, имеющие неодинаковые возможности появления при одном испытании, причем более возможно то событие, которому благоприятствует большее число равновозможных элементарных событий, определяемых испытанием. Тогда возможность появления события Аi, где i изменяется от 1 до 7 удобно измерять отношением  , где n – число всех равновозможных элементарных событий, m – число элементарных событий, благоприятствующих данному событию. , где n – число всех равновозможных элементарных событий, m – число элементарных событий, благоприятствующих данному событию.
Вероятность случайного события А – это число, обозначаемое Р(А). Таким образом, Р(А)=  , где n – общее число исходов данного испытания, m – число исходов, благоприятствующих событию А. , где n – общее число исходов данного испытания, m – число исходов, благоприятствующих событию А.В заданиях ОГЭ и ЕГЭ в основном задачи:
Рассмотрим задачи на определение вероятности подбрасывания монеты. 1 тип: монета подбрасывается один раз Задача 1. Монету подбросили один раз (рис.1). Какова вероятность р о - исходы всего появления «решки»? Рис.1 Дано: A={выпадение «решки»} исходы всего n=21=2 (показатель степени равен числу бросаний) благоприятствующие исходы m=1 Найти: Р(А)=? Решение: Р(А)=  = =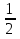 = 0,5 = 0,5Ответ: 0,5 Определение: Событие А называется противоположным событию А, если событие А заключается в том, что событие А не произойдет. Очевидно, что Р(А)+Р(А) =1 Тогда, в задаче 1 противоположным событию А событие А={падение «орла»}. Таким образом, Р(А)=0.5 и Р(А)+Р(А) =1. 2 тип: монета подбрасывается два раза Задача 2. Монету подбросили два раза (рис.1). Какова вероятность появления «решки» один раз? Дано: А={выпадение «решки» один раз»} Р о n=22=4 m= 2 Р о р о -исходы всего Найти: Р(А)=? Рис.2 Решение: Р(А)=  = =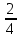 =0.5 =0.5Ответ: 0.5 3 тип: монета подбрасывается более двух раз Задача 3. В эксперименте монету подбрасывают трижды. Найдите вероятность появления орла ровно два раза. A={выпадение «решки» ровно два раза} Дано: n=23=8 Рис. 3 m=3 P o Найти: Р(А)=? Решение: Р(А)=  = =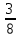 =0.375 =0.375P o p o P o p o p o p o - исходы всего ответ: 0,375 Задача 4. В эксперименте монету подбрасывают трижды. Найдите вероятность появления орла хотя бы один раз. А= {падение орла хотя бы один раз}. Дано: n=8 m=7 Найти: Р(А)=? Решение: Р(А)=  = =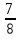 =0.875 =0.875 Ответ: 0,875 Задача 5. В эксперименте монету подбрасывают трижды и замечают, что орел выпал ровно один раз. Найдите вероятность того, что третий раз выпадет «решка». Ответ округлите до сотых. A={выпадение «орла» хотя бы один раз} Дано: n=3 Рис. 4 m=2 P o Найти: Р(А)=? Решение: Р(А)=  = =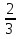 =0,67 =0,67P o p o P o p o p o p o - исходы всего ответ: 0,67 Рассмотрим задачи на определение вероятности подбрасывания кубика. Подбрасываем игральный кубик. Выпасть могут или одно, или два, или три, или четыре, или пять, или шесть очков. Каждый из этих событий элементарное., и вместе они образуют множество элементарных событий. Пусть А={выпадение 5 очков}, B={выпадение четного числа очков}, С={выпадение не менее 3 очков}. Событие А означает выпадение одного из равновозможных элементарных событий; событие В – может выпасть или 2, или 4, или 6. Всего три из шести равновозможных элементарных событий; Событие С - выпадение или 3 очков, или 4, или 5, или 6 очков. Всего 4 из 6 возможных элементарных событий. Тогда Р(А)=  = =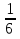 ; Р(В)= ; Р(В)= = =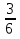 =0.5; Р(С)= =0.5; Р(С)= = =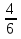 = =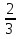 В заданиях ОГЭ и ЕГЭ 2015 года задачи с игральной костью в основном доходят до трех подбрасываний. Рассмотрим 1 тип - когда игральный кубик подбрасывается один раз. Задача 1. Кубик подбросили один раз. Какова вероятность появления 2 очков.
Таб. 1 Таб.1 - число исходов одного подбрасывании я игрального кубика. Тогда число 2 выпадает 1 раз. Дано: Всего исходов n=6 Благоприятствующих исходов m=1 Событие А= {выпадет число 2} Найти: Р(А)=  ? ?Решение: Р(А)=  = =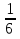 Ответ: Ответ: 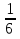 Задача 2. Кубик подбросили один раз. Выпало четное число очков. Какова вероятность появления 2 очков?
Дано: Всего исходов n=3 Благоприятствующих исходов m=1 Событие А= {выпадет число 2 из возможных четных} Найти: Р(А)=  ? ?Решение: Р(А)=  = =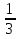 Ответ: Ответ: 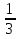 Задача 3. Кубик подбросили один раз. Какова вероятность, что выпадет число очков, большее 2 очков?
Дано: Всего исходов n=6 Благоприятствующих исходов m=4 Событие А= {выпадет число , большее 2} Найти: Р(А)=  ? ?Решение: Р(А)=  = =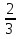 Ответ: Ответ: 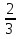 Задача 4. Кубик подбросили один раз. Какова вероятность, что выпадет число очков, не меньшее 2 очков?
Дано: Всего исходов n=6 Благоприятствующих исходов m=5 Событие А= {выпадет число большее или равное 2} Найти: Р(А)=  ? ?Решение: Р(А)=  = =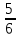 Ответ: Ответ: 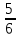 Задача 5. Кубик подбросили один раз. Какова вероятность, что выпадет число очков, менее 2 очков?
Дано: Всего исходов n=6 Благоприятствующих исходов m=1 Событие А= {выпадет число меньшее 2} Найти: Р(А)=  ? ?Решение: Р(А)=  = =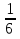 Ответ: Ответ: 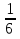 Рассмотрим 2 тип - когда игральный кубик подбрасывается два раза. Задача 1. Игральный кубик подбросили два раза. Какова вероятность, что выпадет в сумме 8 очков?
Дано: Всего исходов n=36 Благоприятствующих исходов m=5 Событие А= {выпадет сумма очков , равное 8} Найти: Р(А)=  ? ?Решение: Р(А)=  = =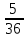 Ответ: Ответ: 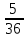 Задача 2. Кубик подбросили два раза. Какова вероятность, что выпадет одинаковое количество очков?
Дано: Всего исходов n=36 Благоприятствующих исходов m=6 Событие А= {выпадет одинаковое количество очков} Найти: Р(А)=  ? ?Решение: Р(А)=  = =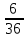 = = 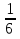 Ответ: Ответ: 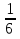 Задача 3. Кубик подбросили два раза. Какова вероятность, что выпадет сначала два, а при втором подбрасывании - 6?
Дано: Всего исходов n=36 Благоприятствующих исходов m=1 Событие А= {выпадет число 2} Найти: Р(А)=  ? ?Решение: Р(А)=  = =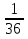 = = 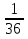 Ответ: Ответ: 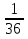 Задача 4. Кубик подбросили два раза. Какова вероятность, что выпали числа, сумма которых меньше 8?
Дано: Всего исходов n=36 Благоприятствующих исходов m=21 Найти: Р(А)=  ? ?Решение: Р(А)=  = =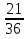 = = 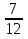 Ответ: Ответ: 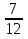 Задача 5. Кубик подбросили два раза. В сумме выпало 8 очков. Найти вероятность того, что при одном из бросков выпадет 5 очков.
Дано: Всего исходов n=5 Благоприятствующих исходов m=2 Событие А= {выпадет число 2} Найти: Р(А)=  ? ?Решение: Р(А)=  = =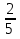 = Ответ: = Ответ: 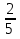 Задача 6. Двое играют в кости - они по разу подбросили игральный кубик. Выигрывает тот, кто у кого больше очков. Если выпадает поровну, то наступает ничья. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того, что он выиграет.
Дано: Всего исходов n=6 Благоприятствующих исходов m=3 Событие А= {первому выпало 4 очка и он выиграет} Найти: Р(А)=  ? ?Решение: Р(А)=  = =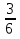 = 0,5 Ответ: = 0,5 Ответ: 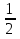 Замечание: При анализе различных версий задания 5 в ЕГЭ-2015 года нет задач с бросанием монеты или кубика три более раз. Решение таких задач не отличаются от решения задач вышеперечисленных задач. Рассмотрим задачи на определение вероятности при выборе одного элемента из множества Рассмотрим задачу: В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном билете обучающемуся достанется вопрос о Великой Отечественной войне. Данная задача относится к задачам выбора одного элемента из множества. Анализируя данную задачу, заключаем, что множеством будет множество билетов по истории. Всего элементов n=50. Множество билетов делится на два подмножества: подмножество, содержащее вопрос о Великой Отечественной войне и подмножество, не содержащее вопрос о ВОВ. Благоприятствующих исходов m=13. Пусть событие А – достался билет с вопросом о ВОВ. Тогда Р(А)= 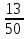 =0,26 ответ: 0,26 =0,26 ответ: 0,26Задача 1. В черном ящике 4 белых и 7 черных шаров. Какова вероятность того, что наудачу вынутый шар окажется белым? Дано: Всего исходов (шаров) n=11 Благоприятствующих исходов m=4 Событие А= {вынут белый шар} Найти: Р(А)=  ? ?Решение: Р(А)=  = =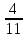 Ответ: Ответ: 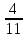 Задача 2. В каждой двадцать пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайным образом. Коля покупает банку в надежде выиграть приз. Найдите вероятность того, что Коля не найдет приз в своей банке. Дано: Всего исходов (банок) n=25 Благоприятствующих исходов m=24 Событие А= {не выиграет приз} Найти: Р(А)=  ? ?Решение: Р(А)=  = =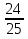 =0,96 Ответ: 0,96 =0,96 Ответ: 0,96Задача 3. Конкурс исполнителей проводится в 3 дня. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день запланировано 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жребием. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Дано: Всего исходов (банок) n=80 Благоприятствующих исходов m=30 Событие А= {россиянин выступит в третий день} Найти: Р(А)=  ? ?Решение: Р(А)=  = =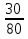 =0,375 Ответ: 0,0,375 =0,375 Ответ: 0,0,375Замечание: При решении данной задачи возникает вопрос – среди участников конкурса есть ли представитель России? Задача, по-моему должна быть уточнена. Например, после слов «- по одному от каждой страны» после запятой дополнит словами « в том числе и из России». Задача 3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых. Решение. Пусть завод произвел N тарелок. В продажу поступят все качественные тарелки и 20% не выявленных дефектных тарелок, т.е. 0,9* N – качественные тарелки, поступающие в продажу и из дефектных тарелок 20% поступают в продажу, т.е. 0,2*0,1* N. Таким образом, в продажу поступаю т n= 0,9* N + 0,2*0,1* N=0.92*N тарелок. Поскольку качественных из них 0.9*N, то вероятность купить качественную тарелку равна: Р(А)= 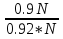 ≈0.98 ≈0.98Ответ: 0,98. Задача 4. Фабрика выпускает сумки. В среднем НА 170 качественных сумок приходится одиннадцать сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется без скрытого дефекта . Результат округлить до сотых. Совет: Когда в задаче встречается союз «НА», то при определении общего количества сумок необходимо суммировать количество качественных и дефектных изделий, т.е. n=170+11=181 Дано: Всего исходов (банок) n=181 Благоприятствующих исходов m=170 Событие А= { купленная качественная сумка без скрытого дефекта } Найти: Р(А)=  ? ?Решение: Р(А)=  = =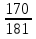 ≈0,92 Ответ: 0,92 ≈0,92 Ответ: 0,92Задача 5. Фабрика выпускает сумки. В среднем ИЗ 100 качественных сумок восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется без скрытого дефекта. Результат округлить до сотых. Совет: Когда в задаче встречается союз «ИЗ», то при определении количества изделий без скрытых дефектов необходимо вычесть из общего количества качественных изделий и количество дефектных изделий, т.е. n=100 - 8=92 Дано: Всего исходов (банок) n=100 Благоприятствующих исходов m=92 Событие А= {купленная качественная сумка без скрытого дефекта} Найти: Р(А)=  ? ?Решение: Р(А)=  = =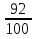 =0,92 Ответ: 0,92 =0,92 Ответ: 0,92Задача 6.В соревнованиях по шахматам, где каждый играет с каждым, участвуют 7 спортсменов из Франции, 6 – из России, 3 – из Японии. Найдите вероятность того, что в первом туре французский спортсмен Жак де Ширак сыграет с другим спортсменов из Франции. Дано: Всего исходов (банок) n=15 ( так как Жак сыграет 15 партий) Благоприятствующих исходов m=6 (Жак сыграет с 6 французами) Событие А= {Жак сыграет с французом} Найти: Р(А)=  ? ?Решение: Р(А)=  = =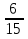 =0,4 Ответ: 0,4 =0,4 Ответ: 0,4Следует заметить, что в заданиях ЕГЭ и ОГЭ присутствуют только задачи на вычисление вероятности в классическом понимании. Также в заданиях отсутствуют задачи при решении которых применяются правила сложения и умножения, выбор нескольких элементов из множества. Поэтому, в данной работе нет необходимости рассматривать перечисленный класс задач. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||