«Множество значений функции». (9 класс)
 Скачать 26.72 Kb. Скачать 26.72 Kb.
|
| Мастер-класс по теме «Множество значений функции». (9 класс) 1.Проверка домашнего задания.На доске изображены графики функций. Ученики должны выбрать и подписать те функции, графики которых построили дома.
2.Игра «Испорченный телефон».Каждая колонка получает задание, где изображены графики функций вида У =f(x +a) +b. Первый ученик записывает функцию, график которой изображен и отрывает предыдущую запись, следующий по формуле изображает график и отрывает и т.д.Выигрывает та колонка, которая первой и верно выполнит задание. Y =(x -2)2 +1; y = 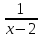 ; y = ; y = 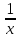 - 2; y = - 2; y =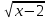 ; y = ; y = 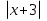 - 1; y = - 1; y =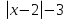 3.Определение свойств функции по заданному графику.На уроках мы часто встречаемся со следующей задачей: Функция задана формулой, требуется исследовать ее свойства и построить график . В жизни происходит иначе: на практике проще получить график физического процесса и по нему изучать свойства. Значительный практический интерес представляет задача: задан график функции, с помощью которого требуется перечислить основные характеристики этой функции. Подобные задачи часто встречаются в ходе экспериментальных исследований. Построение графиков при этом осуществляется разными методами. Например:
4. Устно:Изображен график функции y = f(x)(см. карту урока). По заданному графику необходимо перечислить свойства функции. (Или свойства функции учитель может выписать на доске с некоторыми недочетами. Ученик должен определить ошибки.) 5.Самостоятельная работа в парах на 6 вариантов различной сложности.6.Новый материал.Рассмотрим исследовательские приемы нахождения множества значений функции. Решение задач с параметрами развивает навыки исследовательской деятельности, которые востребованы во многих современных профессиях: логисты, программисты. В данных примерах задание «Найти множество значений функции» можно переформулировать следующим образом: «При каких значениях параметра у уравнение имеет решение?»
Y (x – 4) = 3x + 2 y x – 3x = 2 + 4y x = 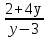 Данное уравнение имеет решение при всех значениях переменной у, кроме у = 3. Ответ: Е(у) = ( -∞;3)U (3;+∞)
Х2 – 3х +2 –у = 0 D =9 – 4(2 –y) 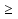 0 0y≥ - 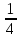 Ответ: Е(у) = 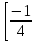 ;+∞) ;+∞)7.Закрепление нового материала:Самостоятельная работа в парах.
У(3х + 5) = 1 х2 + 4х – 1 – y = 0 3ху = 1 – 5у 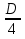 = y + 5 ≥ 0 = y + 5 ≥ 0X = 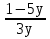 y y 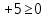 Y ≠ 0 y ≥ - 5 Ответ: Е(у) =(- ∞; 0)U(0;+∞) Ответ: Е(у) = 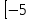 ; +∞) ; +∞)8.Решение примеров повышенной сложности.1) У = 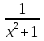 2) у = 2) у = 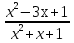 D(y) = ( - ∞; +∞) ух2 + ух + у – х2 + 3х – 1 = 0 Y (x2 + 1) = 1 ( у –1)х2 + ( 3 + у) х + у – 1 = 0 x2 = 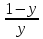 а)если у = 1, то х = 0 а)если у = 1, то х = 0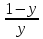 ≥ 0 б) если у ≠ 1, то уравнение имеет ≥ 0 б) если у ≠ 1, то уравнение имеет Ответ: Е(у) =( 0; 1  корни,если D = (3 + у)2 - 4( у – 1)2≥ 0 корни,если D = (3 + у)2 - 4( у – 1)2≥ 0( 5 – у)(3у + 1) ≥ 0 - 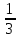 ≤ у ≤ 5 ≤ у ≤ 5Ответ: Е( у) = 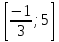 9. Примеры на баллы.( дополнительный материал)1) у = 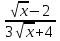 ( 2 балла) Ответ: ( 2 балла) Ответ: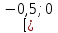 2) у = 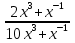 ( 3 балла) Ответ:( ( 3 балла) Ответ:(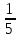 ; 1) ; 1)3) у = 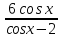 ( 3 балла) Ответ: ( 3 балла) Ответ: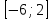 |
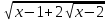 –
– 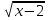
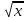 -
- 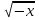
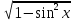 ∙
∙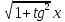 ∙
∙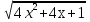
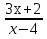
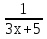 4)у = х2 + 4х – 1
4)у = х2 + 4х – 1