Задание B3 (27545)
 Скачать 114.83 Kb.
|
| Задание B3 (27545) На клетчатой бумаге с клетками размером 1 см 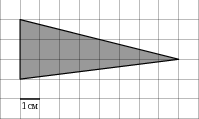 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Задание B3 (27708) Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов 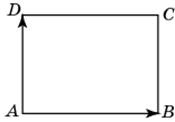 и  . Задание B3 (27560) На клетчатой бумаге с клетками размером 1 см 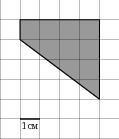1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.  Задание B3 (27704) Найдите площадь треугольника, вершины которого имеют координаты (2, 2), (10, 2), (8, 8). 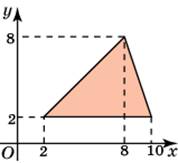 Задание B3 (27614) Задание B3 (27583) Найдите диагональ квадрата, если его площадь равна 2. 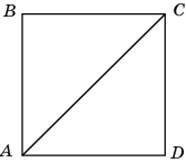 Задание B3 (27615) Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. 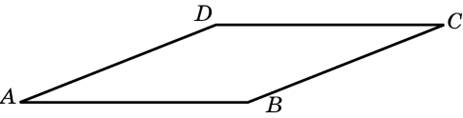 Задание B3 (27554) На клетчатой бумаге с клетками размером 1 см 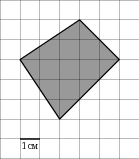1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Задание B3 (27544) На клетчатой бумаге с клетками размером 1 см 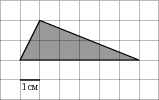1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Задание B3 (27547) На клетчатой бумаге с клетками размером 1 см 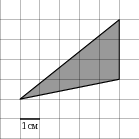1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Задание B3 (27578) Найдите площадь параллелограмма, изображенного на рисунке.  Задание B3 (27668) Найдите угловой коэффициент прямой, проходящей через точки с координатами (2, 0) и (0, 2). 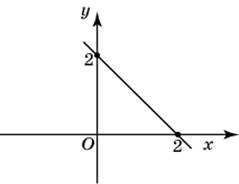 Задание B3 (27674) Точки O(0, 0), A(6, 8), B(4, 2) и C являются вершинами параллелограмма. Найдите ординату точки C. 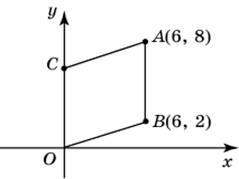 Задание B3 (27692) Окружность с центром в начале координат проходит через точку P(8, 6). Найдите ее радиус. 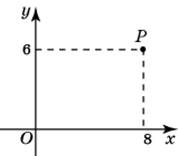 Задание B3 (27649) Найдите расстояние от точки A с координатами (6, 8) до оси абсцисс. 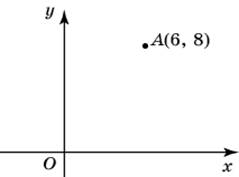 Задание B3 (27582 Найдите площадь квадрата, если его диагональ равна 1. 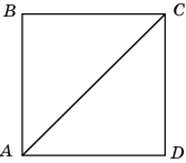 Задание B3 (27632) Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции. 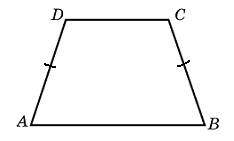 Задание B3 (27661) Найдите длину отрезка, соединяющего точки O(0, 0) и A(6, 8). 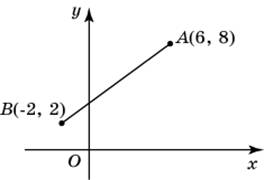 Задание B3 (275 Найдите площадь закрашенной фигуры на координатной плоскости. 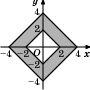 Задание B3 (27634) Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и . Задание B3 (27636) Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции. Задание B3 (27651) Найдите расстояние от точки A с координатами (6, 8) до начала координат. 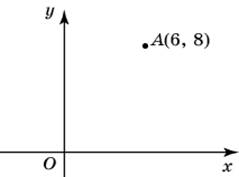 Задание B3 (27579) Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (4;6), (4;8), (1;9).  Задание B3 (27654) Найдите абсциссу точки, симметричной точке A(6, 8) относительно начала координат. 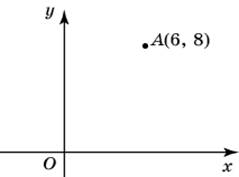 Задание B3 (27652) Найдите абсциссу точки, симметричной точке A(6, 8) относительно оси Oy. Задание B3 (27667) Найдите угловой коэффициент прямой, проходящей через точки с координатами (-2, 0) и (0, 2). 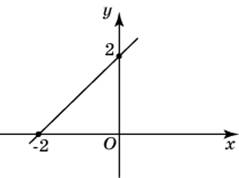 Задание B3 (27728) Вектор 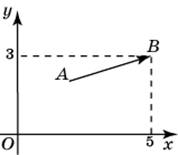с концом в точке B(5, 3) имеет координаты (3, 1). Найдите ординату точки A. Задание B3 (27686) Точки O(0, 0), A(10, 0), B(8, 6), C(2, 6) являются вершинами трапеции. Найдите длину ее средней линии DE. 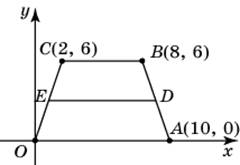 Задание B3 (27572) Найдите площадь трапеции, изображенной на рисунке. 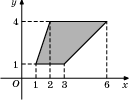 Задание B3 (27591) Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30 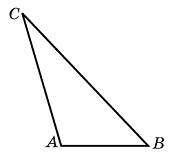 . Задание B3 (27682) Точки O(0, 0), B(8, 2), C(2, 6) и A являются вершинами параллелограмма. Найдите ординату точки A. 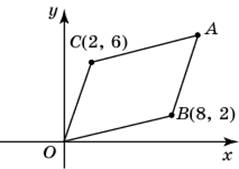 Задание B3 (27597) Площадь круга равна  . Найдите длину его окружности. Задание B3 (27679) Точки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C. 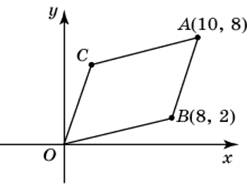 Задание B3 (27724) Вектор 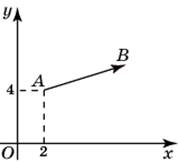с началом в точке A(2, 4) имеет координаты (6, 2). Найдите абсциссу точки B. Задание B3 (27698) Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6). 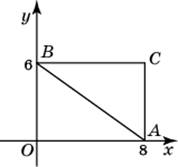 Задание B3 (27688) Найдите ординату точки пересечения прямой, заданной уравнением 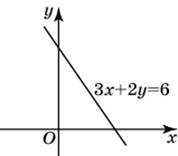 , с осьюOy. Задание B3 (27564) Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9). 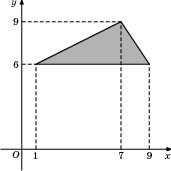 Задание B3 (27566) Точки O(0, 0), B(6, 2), C(0, 6) и A являются вершинами параллелограмма. Найдите ординату точки A. 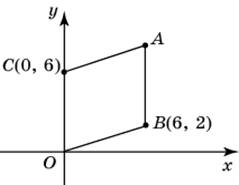 Задание B3 (27650) Найдите расстояние от точки A с координатами (6, 8) до оси ординат. Задание B3 (27561) На клетчатой бумаге с клетками размером 1 см 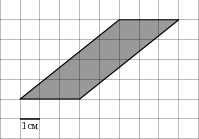1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите  . Задание B3 (27599) Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2. 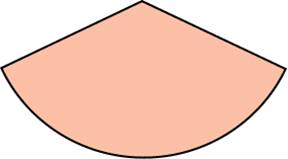 Задание B3 (27733) Найдите квадрат длины вектора 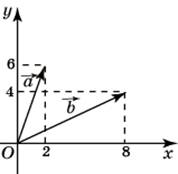 . Задание B3 (27656) Найдите ординату середины отрезка, соединяющего точки O(0, 0) и A(6, 8). 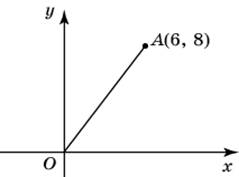 Задание B3 (27608) Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов. 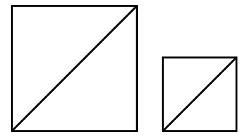 Задание B3 (27628) Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции. 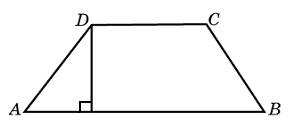 Задание B3 (27691) Найдите угловой коэффициент прямой, заданной уравнением 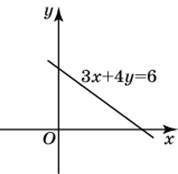 . Задание B3 (27626) Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности. 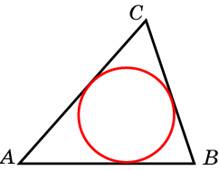 Задание B3 (27715) Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора 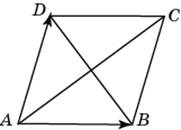 . Задание B3 (27606) ( Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника. 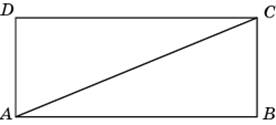 Задание B3 (27642) Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 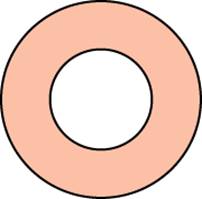 и  . Задание B3 (27602) Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1 : 2.  Задание B3 (27629) Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции. 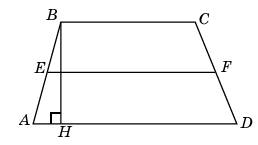 Задание B3 (27655) Найдите ординату точки, симметричной точке A(6, 8) относительно начала координат. Задание B3 (27634) Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. 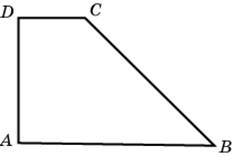 Задание B3 (27653) Найдите ординату точки, симметричной точке A(6, 8) относительно оси Ox. Задание B3 (27727) Вектор 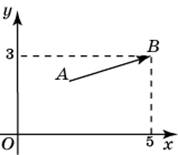с концом в точке B(5, 3) имеет координаты (3, 1). Найдите абсциссу точки A.  Задание B3 (27726) Вектор 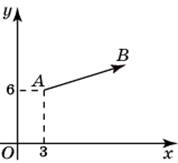с началом в точке A(3, 6) имеет координаты (9, 3). Найдите сумму координат точки B.  Задание B3 (27685) Точки O(0, 0), A(6, 8), B(8, 2) являются вершинами треугольника. Найдите длину его средней линии CD. 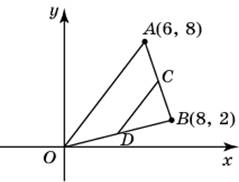 Задание B3 (27589) Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30 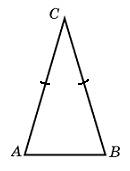. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.  Задание B3 (27593) Основания трапеции равны 1 и 3, высота 1. Найдите площадь трапеции. 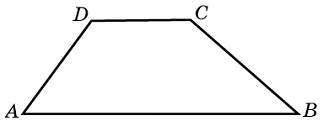 Задание B3 (27665) Найдите синус угла наклона отрезка, соединяющего точки O(0, 0) и A(6, 8), с осью абсцисс. 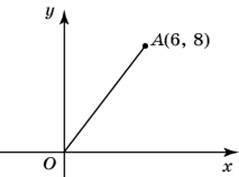 Задание B3 (27676) Точки O(0, 0), A(6, 8), B(6, 2), C(0, 6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей. 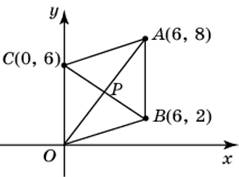 Задание B3 (27543) На клетчатой бумаге с клетками размером 1 см 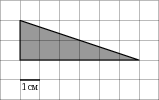1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Задание B3 (27603) Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2. Задание B3 (27551) Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1. 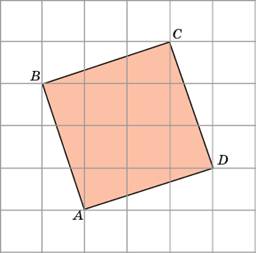 Задание B3 (27648) Через точку  (6, 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.Задание B3 (27568) Найдите площадь прямоугольника, вершины которого имеют координаты (1;1), (10;1), (10;7), (1;7).  Задание B3 (27549) На клетчатой бумаге с клетками размером 1 см 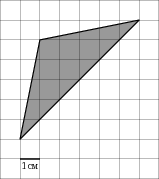1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Задание B3 (27556) На клетчатой бумаге с клетками размером 1 см 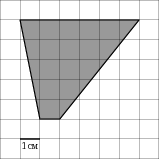1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Задание B3 (27694) Какого радиуса должна быть окружность с центром в точке P(8, 6), чтобы она касалась оси ординат? 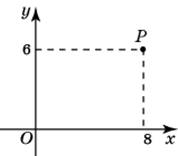 Задание B3 (27721) Стороны правильного треугольника ABC равны 3. Найдите длину вектора 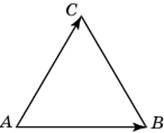 . Задание B3 (27693) Какого радиуса должна быть окружность с центром в точке P(8, 6), чтобы она касалась оси абсцисс? |