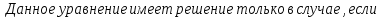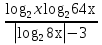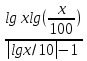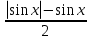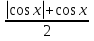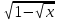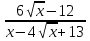Примеры, сводящиеся к замене переменных и исследованию получившейся функции на заданном промежутке.
Найти множество значений функции у = 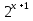 -
- 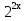
Решение:
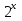
= t , t > 0
g(t) = 2t – t
2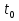
= 1;
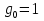
Ответ: Е(у) = (- ∞; 1]
Найти наименьшее значение функции
у = ( х
2 – х + 1)( х
2 – х + 2)
Решение:
x
2 – х = t , t ≥ -
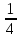
Исследуем функцию g(t) = ( t + 1)(t + 2) на [
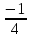
; +∞
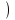
g(t) = t
2 + 3t + 2
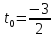
не принадлежит промежутку [-
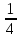
; +∞)
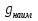
= g(-
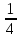
) =
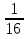
- 3∙
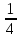
+ 2=
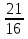
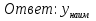 =
=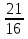
Найти множество значений функции
y = cos2x – 4cosx
Решение:
У=2cos
2x– 4cosx-1
Пусть соs x = t, -1
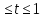
g(t) = 2t
2 – 4t – 1
t
0=1
g(1) = - 3
g(-1)= 5
Ответ: E(y) = [-3;5]
Найти множество значений функции
У=
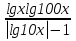
Решение:
ООФ(0;0,01)U(0,01;1)U(1;∞)
Пусть lgx = t, , t≠0,t ≠ -2
g(t)=
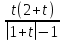
g(t)=
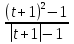
g(t)=
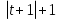
Учитывая, что t≠0,t ≠ -2, получаем Е(у)=[1;2)U(2;∞)
Ответ: Е(у)=[1;2)U(2;∞)
5) Найти наибольшее значение функции
у = х +log
2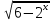
Решение:
Пусть 2
х = t, 0
x= log
2t
y(t)= log
2t + log
2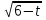
y(t)= log
2(t
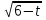
)
y(t)= log
2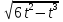
Рассмотрим функцию g(t) = 6t
2 – t
3 на (0;6)
g
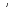
(t) = 12t – 3t
23t(4-t) = 0
g
наиб= g(4) =6∙16 – 64 = 32
y
наиб=log
2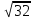
=
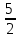
Ответ:
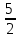
6) Найти множество значений функции
y = 3cos2x + 4sin2x + 4sinx + 8cosx
Решение:
Y = 5cos(2x – α) + 4
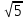
cos(x – β)
tg α =
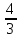
; tg β =
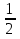
tg2 β =
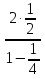
=
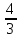
α = 2β
у = 5 cos(2x – 2β) + 4
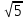
cos(x – β)
у = 5(2cos
2(x –β) - 1) + 4
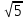
cos(x – β)
Пусть cos(x – β)= t,
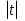
≤1
y = 5(2t
2 – 1) +4
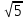
t
y =10t
2+4
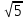
t – 5
t
0= -
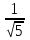
y(-
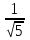
) = -7
y(-1)= 5 - 4
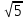
y(1) = 5 + 4
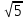
E(y) = [-7; 5 + 4
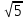
]
Ответ: E(y) = [-7; 5 + 4
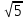
]
7) Найти множество значений функции
у =
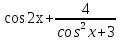
Решение:
t= cos
2x + 3, 3≤ t ≤4
cos2x = 2cos
2x – 1 = 2t – 7
y = 2t +
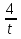
- 7
y’= 2 -
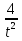
y’ > 0 на [3; 4]
у(3) =
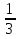
; у(4) = 2
Ответ: Е(у) =[
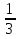
; 2]
Примеры, сводящиеся к решению уравнения с параметром.
1) Найти множество значений функции у =
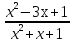
Решение:
Выясним, при каком значении параметра «у» данное уравнение имеет решение.
у(х
2+х+1) = х
2-3х+1
(1-у)х
2 – (3+у)х + 1 – у = 0
Если у = 1,то 0х2 – 4х + 1 -1 = 0, х=0
Если у ≠1, то квадратное уравнение имеет корни, если D≥0
D = - 3y
2 + 14y + 5.
- 3y
2 + 14y + 5≥0
у ≠1
Решив данную систему неравенств, получим
-
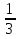
≤у<1; 1
Учитывая, что при у=1 уравнение имеет решение, получаем ответ: Е(у)= [-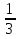 ; 5]
; 5]
Ответ: Е(у)= [-
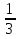
; 5]
2) Найти множество значений функции
У=
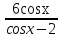
Решение:
ycos x – 2y = 6cosx
(y- 6) cosx = 2y
сosx =
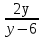
1 ≤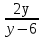 ≤ 1
≤ 1
Решив
данное неравенство, получим - 6 ≤у ≤2
Ответ: Е(у) = [- 6; 2]
Найти множество значений функции
у = х
4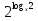
Решение:
D(y) = (0; 1)U(1;+∞)
Выясним, при каком значении параметра у данное уравнение имеет решение.
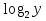
= 4
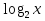
+
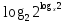
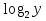
- 4
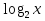
-
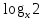
= 0
Пуст
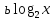
= t
Квадратное уравнение 4t
2 -
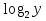
t + 1 = 0 имеет решения, если D≥0
D = log
22y – 16 ≥0
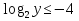
или
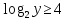
0
y ≥ 16
Ответ: Е(у) = (0 ; 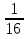 ]U[16;∞)
]U[16;∞)
Найти множество значений функции у = 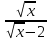
Решение:
y(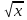 - 2) =
- 2) = 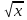
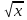 =
= 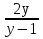
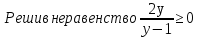 , получим у ≤ 0; у > 1
, получим у ≤ 0; у > 1
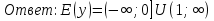
Использование неравенства a + 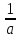 ≥ 2, а>0
≥ 2, а>0
Найти наименьшее значение функции
у =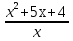 , где х>0
, где х>0
Решение:
У = х + 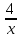 + 5
+ 5
У = 2(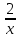 +
+ 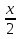 ) + 5
) + 5
Унаим= 9
Ответ:9
Найти наименьшее значение функции
у = 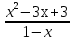 , если х < 1
, если х < 1
Решение:
У = 1 – х + 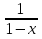 + 1
+ 1
Так как 1 – х + 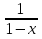 ≥ 2 при условии х < 1, то унаим = 3
≥ 2 при условии х < 1, то унаим = 3
Ответ: унаим = 3
Решить уравнение:
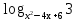 +
+ 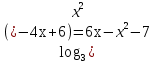
Решение:
X2- 4x + 6 = (х – 2)2 + 2 > 1, следовательно, 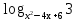 >0,
>0,
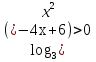 , так как , если a>1, b>1, то
, так как , если a>1, b>1, то 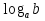 >0
>0
Таким образом,
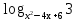 +
+ 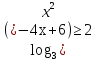 (сумма двух взаимно обратных положительных чисел всегда не меньше 2)
(сумма двух взаимно обратных положительных чисел всегда не меньше 2)
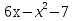 = - ( х2 – 6х + 9) + 2 = - ( х – 3)2 + 2 ≤ 2
= - ( х2 – 6х + 9) + 2 = - ( х – 3)2 + 2 ≤ 2 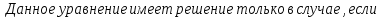
л.ч. = пр.ч.= 2
-х2 + 6х -7 = 2
х2 - 6х +9 = 0
х = 3
Подставив х = 3 в левую часть уравнения, убедимся, что х = 3 является корнем данного уравнения
Ответ: 3
Найти множество значений функций:
Замена переменных и исследование функции на промежутке
|
Ответ
|
Решение уравнения с параметром
|
Ответ
|
y = сos2x + cosx
y=2sin2x – sinx
y = 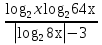
y =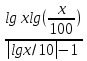
y=cos((πsinx)/3)
y=sin((πcos)/4)
y=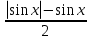
y=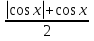
y= 2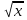 - -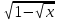
10)y= - 2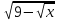 - -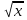
11)y=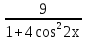 +2cos4x +2cos4x
12) y=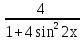 - 2cos4x - 2cos4x
|
[-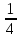 ;2] ;2]
[-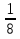 ;3] ;3]
[3;6)U(6;∞)
[1;2)U(2;∞)
[1/2;1]
[-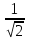 ; ;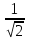 ] ]
[0;1]
[0;1]
[-1;2]
[-10;-6]
[3;7]
[1;14/5]
|
1)y = 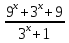
2)y =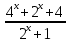
y= 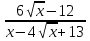
4)y=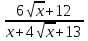
5)y=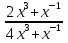
6)y=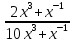
7)y=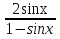
8)y=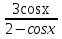
9)y=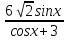
10)y=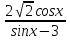
11)y=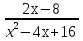
12)y=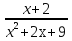
|
[5;∞)
[3;∞)
[-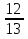 ;1] ;1]
(0;1]
(1/2;1)
(1/5;1)
[-1;∞)
[-1;3]
[-3;3]
[-1;1]
[-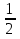 ; ;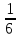 ] ]
[-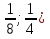
|
 Скачать 78.37 Kb.
Скачать 78.37 Kb.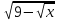 -
-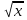
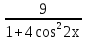 +2cos4x
+2cos4x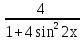 - 2cos4x
- 2cos4x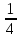 ;2]
;2]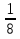 ;3]
;3]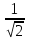 ;
;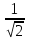 ]
]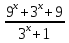
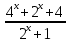
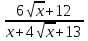
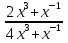
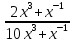
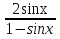
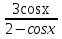
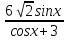
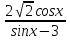
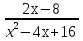
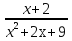
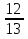 ;1]
;1]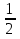 ;
;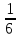 ]
]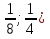
 Множество значений функции.
Множество значений функции.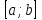 и
и 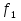 (x)= c f(x), где с = const, то
(x)= c f(x), где с = const, то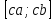 при с > 0 или
при с > 0 или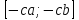 при с < 0.
при с < 0.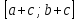 .
.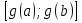 , g – возрастающая функция на
, g – возрастающая функция на 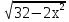 .
.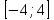
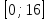 .
.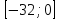
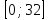 .
.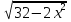 ) =
) = 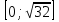 .
.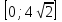
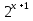 -
- 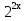
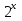 = t , t > 0
= t , t > 0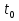 = 1;
= 1; 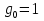
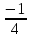 ; +∞
; +∞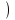
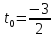 не принадлежит промежутку [-
не принадлежит промежутку [-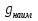 = g(-
= g(-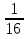 - 3∙
- 3∙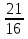
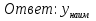 =
=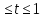
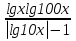
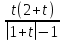
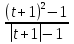
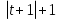
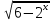
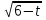
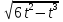
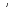 (t) = 12t – 3t2
(t) = 12t – 3t2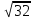 =
= 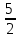
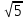 cos(x – β)
cos(x – β)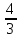 ; tg β =
; tg β = 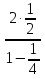 =
= 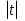 ≤1
≤1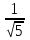
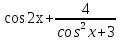
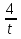 - 7
- 7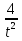
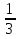 ; у(4) = 2
; у(4) = 2 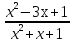
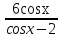
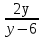
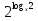
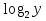 = 4
= 4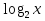 +
+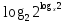
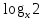 = 0
= 0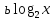 = t
= t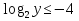 или
или 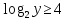
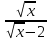
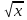 - 2) =
- 2) = 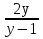
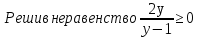 , получим у ≤ 0; у > 1
, получим у ≤ 0; у > 1 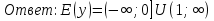
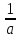 ≥ 2, а>0
≥ 2, а>0 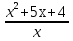 , где х>0
, где х>0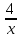 + 5
+ 5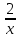 +
+ 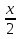 ) + 5
) + 5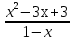 , если х < 1
, если х < 1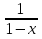 + 1
+ 1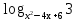 +
+ 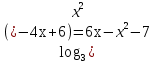
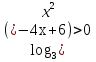 , так как , если a>1, b>1, то
, так как , если a>1, b>1, то 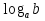 >0
>0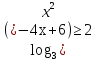 (сумма двух взаимно обратных положительных чисел всегда не меньше 2)
(сумма двух взаимно обратных положительных чисел всегда не меньше 2)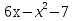 = - ( х2 – 6х + 9) + 2 = - ( х – 3)2 + 2 ≤ 2
= - ( х2 – 6х + 9) + 2 = - ( х – 3)2 + 2 ≤ 2