Открытое занятие по элективному курсу по алгебре для 9 классов «Функции и их графики»
 Скачать 35.35 Kb. Скачать 35.35 Kb.
|
| Открытое занятие по элективному курсу по алгебре для 9 классов «Функции и их графики» Цели: - повторить определения функций и графиков функций; - закрепить и изучить глубже функцию у=│х│; - развивать у учащихся умения и навыки по решению задач с графиками; Ход занятия.
УЧ. Здравствуйте, ребята. Сегодня у нас очередное занятие элективного курса: «Функции и их графики». Китайская пословица гласит: «Я слушаю – я забываю; Я вижу – я запоминаю; Я делаю – я усваиваю…» Итак, чтобы хорошо запомнить материал, усвоить его мы далеко от этой пословицы постараемся не отходить. На данном уроке мы повторим и закрепим тем самым пройденный материал, так как мы приближаемся уже к концу курса, рассмотрим глубже функцию у=f│x│.
Учащиеся отвечают на поставленные вопросы. Приводят примеры. УЧ. Хорошо, ребята. Давайте разберем конкретнее изученные нами функции по нашей презентации. Презентация.
УЧ. Ребята, давайте остановимся на линейной функции. Вспомним еще раз ее свойства.Презентация (продолжение)
1)достроить и найти точку пересечения; 2) решить уравнение 0,9х+1=0,8х+1.
Когда к>0, функция возрастает, с осью Ох образует острый угол, если к<0, убывает, с осью Ох образует тупой угол. УЧ. Молодцы, ребята. Теперь рассмотрим квадратичную функцию, ее график, преобразования.(Презентация «Квадратичная функция»). Учащиеся разбирают, отвечают на вопросы преподавателя.
УЧ. Молодцы, ребята. Для закрепления поработайте заданиями (самоконтроль). Презентация «Задания по квадратичной функции» . Учащиеся выполняют 3-4 мин.
УЧ. С заданиями справились. Теперь подробнее рассмотрим функцию у=│х│. Что мы понимаем под понятием модуль? Каков график функции? График находится в 1 и 2 четвертях. Почему?    
УЧ. Давайте, ребята, посмотрим, как работать с графиком у=│х│. ПРИМЕРЫ: 1) Построить графики функции у=│х-2│, у=│х-3│-1. Как поведет себя график? УЧ. Принцип сдвига графика такой же, как и квадратичной функции. V. Упражнения на закрепление. 2) Построим графики функций у=2│х│,у=│х│+ │х-2│; у=│х+1│-│х│; 3) Какой график получится при построении функции у=││х│-1│; 4) у=│х2-4х│;
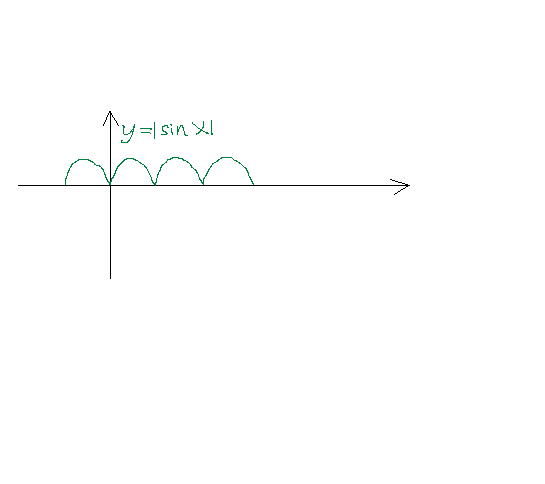 2)Любишь кататься, люби и саночки возить. 2)Любишь кататься, люби и саночки возить.
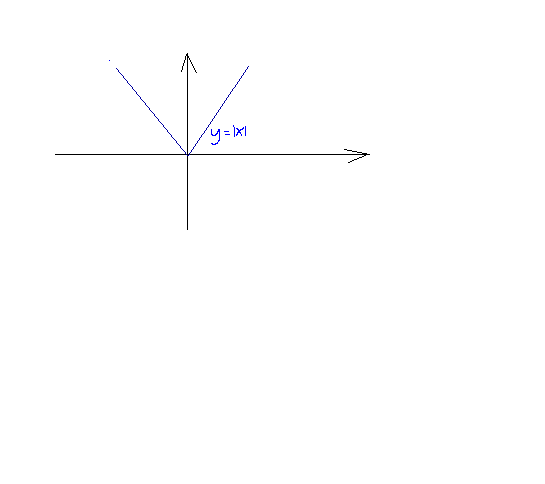 УЧ. Дома поработайте по карточкам, которые я вам раздам. (по 10 заданий). СПАСИБО ЗА УРОК!!! ДО СВИДАНИЯ!!! |