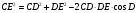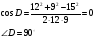|
Пособие по решению задач по теме: «Трапеция и ее свойства» Составитель С. В. Дунай Преподаватель математики Москва 2014

ПОСОБИЕ ПО РЕШЕНИЮ ЗАДАЧ
по теме: «Трапеция и ее свойства»
Составитель С.В.Дунай
Преподаватель математики
Москва 2014.
СОДЕРЖАНИЕ.
Теоретическая часть:
- определение трапеции и ее свойства;
- виды трапеций;
- линии параллельные основаниям (средняя линия; линия,делящая площадь трапеции на равновеликие части; линия,проходящая через точку пересечения диагоналей);
- трапеция, вписанная в окружность;
- трапеция,описанная около окружности;
- площадь трапеции.
2. Примеры решения задач.
3. Самостоятельная работа
4. Ответы.
Трапеция. Площадь трапеции.
Трапеция — четырехугольник, у которого ровно одна пара противолежащих сторон параллельна.
Параллельные стороны называются основаниями трапеции.
Две другие стороны называются боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Расстояние между основаниями называется высотой трапеции.
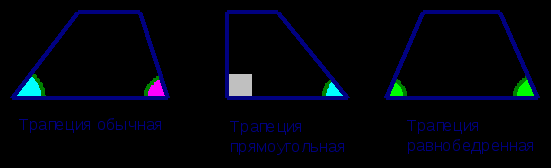
Трапеция, у которой боковые стороны равны, называется равнобокой (или равнобедренной)
Трапеция, один из углов которой прямой, называется прямоугольной.
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Свойства трапеции:
в равнобокой трапеции углы при основании равны;
в равнобокой трапеции диагонали равны;
Средняя линия трапеции обладает свойством – она параллельна основаниям трапеции и равна их полусумме.
Если трапеция равнобокая, то около нее можно описать окружность.
Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.
В трапеции середины оснований, точка пересечения диагоналей и продолжения боковых сторон находятся на одной прямой.
Виды трапеций.
Линии параллельные основаниям Средняя линия
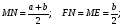 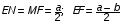
Линия, проходящая через точку пересечения диагоналей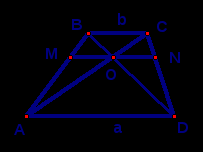
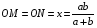 или или 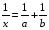
Линия, делящая площадь трапеции на равновеликие части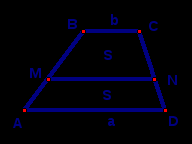
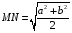
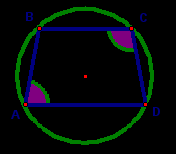
Трапеция, вписанная в окружность
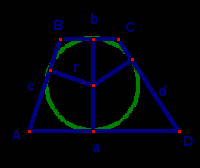
Трапеция, описанная около окружности
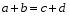
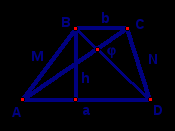
Площадь трапеции.
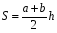 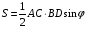
Пример 1. Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание.
Решение.
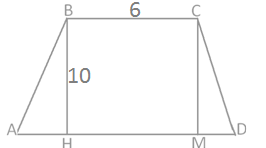
BC=6, ВH=10, tgA = 2.
Выполним дополнительно построение: проведем вторую высоту CM.
Рассмотрим основание трапеции AD. Его длина складывается из длин отрезков: AD=AH+HM+MD. Обратим внимание, что так как трапеция равнобедренная, то АВН = CMD (по гипотенузе и углу) AH= MD, кроме этого ВС=HM.
Переходим к использованию данных задачи: AD=2x + 6, где x – длина отрезка AH. Так как tgA =2, то 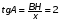 (тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету). Следовательно, x = 10/2 = 5. (тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету). Следовательно, x = 10/2 = 5.
Окончательно получаем AD= 2x + 6 = 16.
Ответ: 16
Пример 2. На клетчатой бумаге с клетками размером 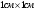 изображена трапеция. Найдите ее площадь в квадратных сантиметрах. изображена трапеция. Найдите ее площадь в квадратных сантиметрах.
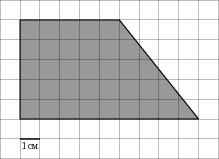
Решение. Обратимся к рисунку. Следует заметить, что площадь выделенной фигуры можно представить в виде сумме площадей квадрата (располагается слева) и прямоугольного треугольника (располагается справа).
Площадь квадрата S = a2, где а – длина стороны квадрата. Площадь прямоугольного треугольника 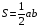 , где а и b – катеты прямоугольного треугольника. , где а и b – катеты прямоугольного треугольника.
Переходим к вычислительной части решения задачи. 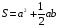 . Исходя из рисунка а=5 см., в=4 см. Следовательно, . Исходя из рисунка а=5 см., в=4 см. Следовательно, 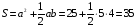 см. см.
Ответ: 35.
Пример 3. В равнобедренной трапеции основания 21 и 9 сантиметров, высота – 8 сантиметров. Найти радиус описанной окружности.
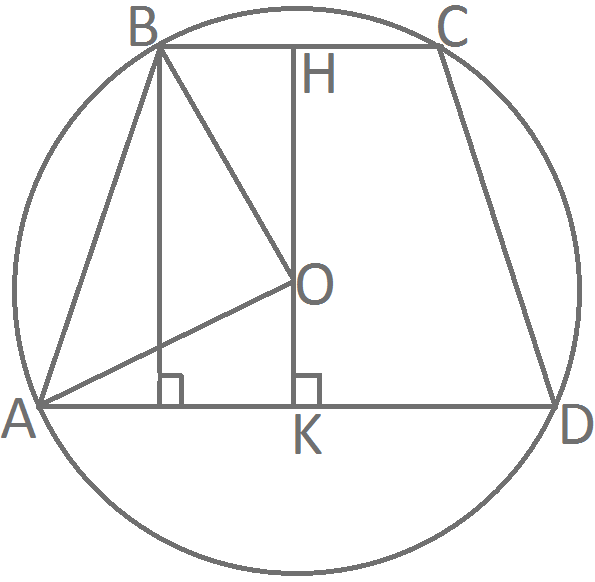
Решение.
Проведем серединный перпендикуляр к основаниям НК, тогда центр окружности О лежит на прямой НК.
АО = ОВ = R. Точка О делит отрезок НК на две части: пусть НО = х, тогда ОК = 8 – х.
АО2 = АК2 + КО2; ОВ2 = ВН2 + НО2.
Так как ОА2=ОВ2, получим: АК2 + КО2 = ВН2 + НО2
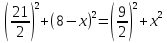
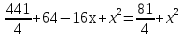
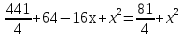
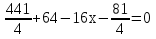
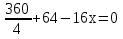
90 + 64 – 16x = 0
16x = 154
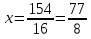
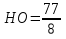
ОВ2 = ВН2 + НО2
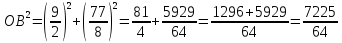
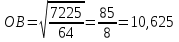
Ответ: R = 10,625.
Пример 4. Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD – равнобедренная трапеция, r = 4, AB = 10
Найти: 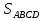
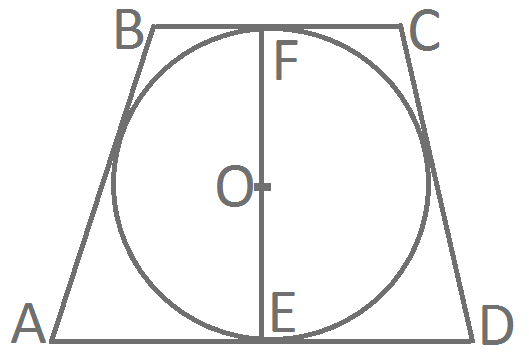
AB = CD = 10 по условию
AB + CD = AD + BC по свойству вписанной окружности
AD + BC = 10 + 10 = 20
FE = 2r = 2 · 4 = 8
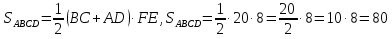
Ответ: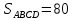 . .
Пример 5. Основания трапеции равны 10 м и 31 м, а боковые стороны – 20 м и 13 м. Найдите высоту трапеции.

Решение.
Пусть HK = BC = 10 м, BH = CK = x, AH=y, тогда KD = 21 – y
По теореме Пифагора:
x2 + y2 = 132
x2 + (21 – y)2 = 202
x2 + y2 = 169 (1)
x2 + 441 – 42y + y2 = 400 (2)
Вычтем из (2) уравнения (1):
441 – 42y = 231
42y = 210
y = 5
AH = 5 м
По теореме Пифагора:
BH2 = AB2 – AH2
BH2 = 132 – 52
BH2 = 169 – 25
BH2 = 144
BH = 12
Ответ: BH = 12.
Пример 6. Большее основание трапеции равно 24. Найдите длину меньшего основания, если расстояние между серединами диагоналей равно 4.
Решение.
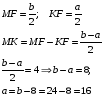 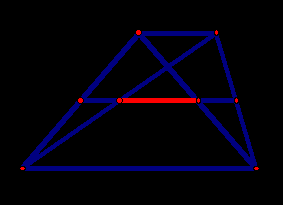
Ответ: 16.
Пример 7. В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны боковым сторонам. Найдите площадь трапеции.
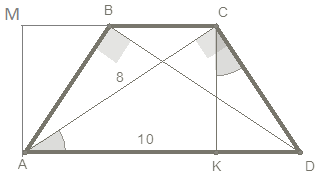
Анализ. Длины диагоналей равны и перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников по катету и гипотенузе: ABD = ACD, поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для определения боковой стороны трапеции.
Высоту трапеции определим из равенства площадей.
Проекцию боковой стороны на большее основание легче определить из подобия треугольников, чем по теореме Пифагора.
Длину средней линии в равнобокой трапеции можно определять как разность большего основания и проекции боковой стороны на основание.
Площадь трапеции находим как площадь прямоугольника АМСК, который получим, если достроим трапецию.
Решение.
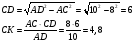
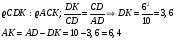
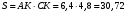
Ответ: 30,72.
Пример 8. Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9. Найдите длину отрезка, соединяющего середины оснований трапеции.
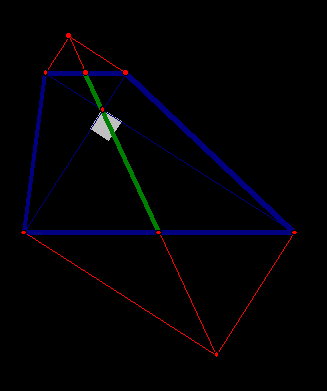
Анализ. Задача решается построением.
Достроим прямоугольники и используем свойство прямоугольника: диагонали прямоугольника равны и в точке пересечения делятся пополам.
Длина средней линии равна полусумме длин оснований.
Длина отрезка, соединяющая середины оснований, равна полусумме длин диагоналей двух построенных треугольников.
Решение.
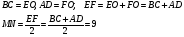
Ответ: 9.
Пример 9. Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного основаниям и заключенного между боковыми сторонами, который делит трапецию на две равновеликие части.
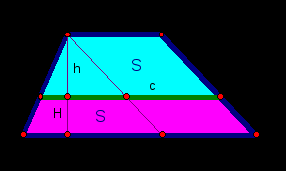
Анализ. Провести из вершины тупого угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей трапеций.
Определить отношение при подобии треугольников.
Рациональные алгебраические преобразования приведут к результату.
Решение.
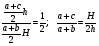

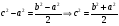
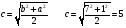
Ответ: 5.
Пример 10. Равнобедренная трапеция ABCD описана около окружности. Боковая сторона трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
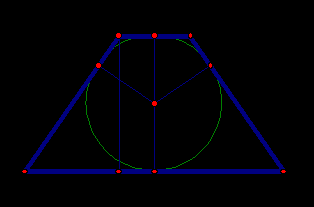
Анализ. Сумма противоположных сторон трапеции равна между собой – свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине средней линии.
Применяем теорему Пифагора для нахождения высоты трапеции.
Площадь трапеции определяем по доступной формуле.
Решение.
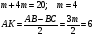
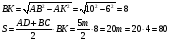
Ответ: 80.
Пример 11. Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.
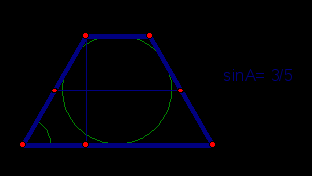
Анализ. Трапеция равнобедренная.
Длина средней линии равна боковой стороне.
Площадь трапеции определяется произведением средней линии на высоту трапеции.
Опустим высоту трапеции из тупого угла. Через заданный косинус угла определим синус угла. По синусу угла выразим высоту трапеции через боковую сторону.
Решение.
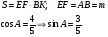
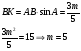
Ответ: 5.
Пример 12. В прямоугольной трапеции, описанной около окружности, большая боковая сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание трапеции.
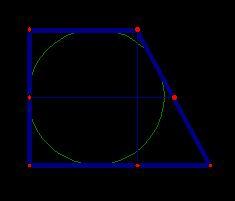
Анализ. Необходимо использовать свойство сторон четырехугольника, описанной около окружности: сумма длин противоположных сторон равна между собой.
Кроме того, длина средней линии равна полусумме длин сторон оснований.
Проведем из вершины тупого угла высоту трапеции.
Воспользуемся теоремой Пифагора и определим проекцию наклонной боковой стороны на основание.
Решение.
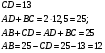
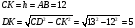
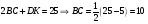
Ответ: 10.
Пример 13. В равнобедренную трапецию, один из углов которой равен 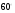 , а площадь равна , а площадь равна 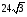 , вписана окружность. Найдите радиус этой окружности. , вписана окружность. Найдите радиус этой окружности.
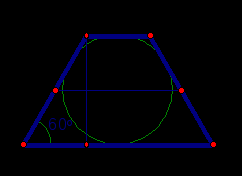
Анализ. Важное положение, что трапеция является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны равна длине средней линии.
Введем параметр боковой стороны, из прямоугольного треугольника по заданному углу определим высоту трапеции, которая является диаметром вписанной окружности. Площадь трапеции определяется как произведение средней линии на высоту трапеции.
Решение.
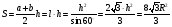
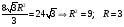
Ответ: 3
Пример 14. Трапеция 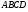 вписана в окружность. Найдите среднюю линию трапеции, если ее большее основание вписана в окружность. Найдите среднюю линию трапеции, если ее большее основание 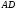 равно 15, синус угла равно 15, синус угла 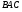 равен равен 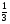 , синус угла , синус угла 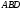 равен равен 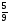 . .
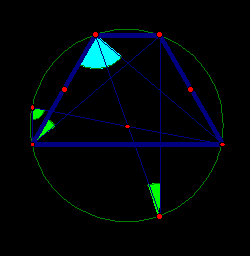
Анализ. Трапецию можно вписать в окружность, если она равнобедренная.
Длина любой хорды определяется из теоремы синусов.
Решение.
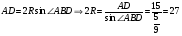
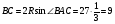
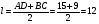
Ответ: 12.
Пример 15. Боковые стороны 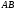 и и 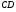 трапеции трапеции 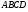 равны 15 и 12 соответственно. Найдите градусную величину угла равны 15 и 12 соответственно. Найдите градусную величину угла 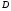 , если одно из оснований трапеции на 9 больше другого. , если одно из оснований трапеции на 9 больше другого.

Анализ. Из вершины угла 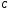 проведем прямую линию, параллельную стороне проведем прямую линию, параллельную стороне 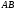 . .
Трапеция разделена данной прямой линией на параллелограмм и треугольник.
Противоположные стороны параллелограмма равны, значит, длина стороны треугольника равна разности длин оснований трапеции.
Данный треугольник определен по трем сторонам.
По теореме косинусов определим искомый угол.
Вычисления показывают, что боковая сторона перпендикулярна к основанию, искомый угол прямой.
Решение.
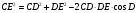
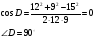
Ответ: 90.
САМОСТОЯТЕЛЬНАЯ РАБОТА.
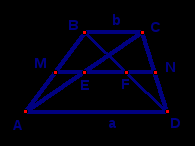
Точки А и В – середины диагоналей трапеции KPNМ. Найти длину меньшего основания PN, если AB = 5 и KM = 16.
ОТВЕТ: 6.
Точки M и N – середины диагоналей трапеции ABCD. Найти длину отрезка MN, если основания трапеции AD = 10 и BC = 4.
ОТВЕТ: 3.
Диагонали АС и BD трапеции ABCD пересекают среднюю линию в точках К и Е соответственно. Если AD = 12 см, ВС = 8 см, то отношение МК : МЕ равно
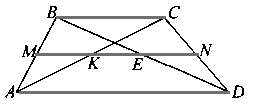
ОТВЕТ: 2:3
В прямоугольной трапеции меньшее основание 4, большая боковая сторона 12, а угол при основании 300. Найти площадь трапеции.
ОТВЕТ: 183 + 24
Точки Р и К – середины диагоналей трапеции ABCD. Найти длину средней линии трапеции, если длина основания ВС = 5, а отрезка РК = 8.
ОТВЕТ: 13
В треугольнике АВС точки Р и Е – середины сторон АВ и ВС соответственно, точки М и Н – середины отрезков АР и СЕ соответственно. Если РЕ =11 см, то отношение АС : МН равно
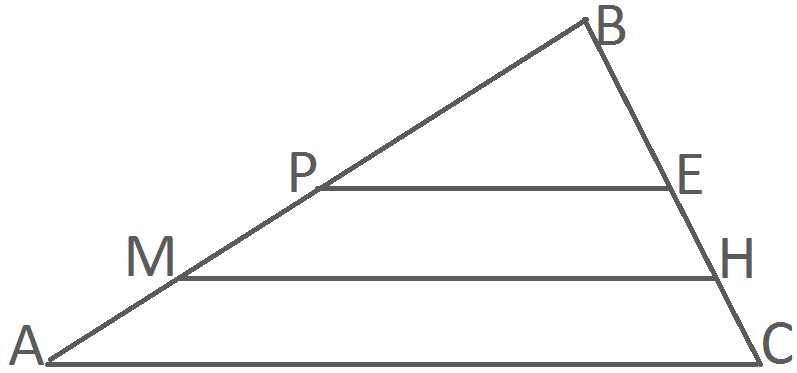
ОТВЕТ: 4:3
В треугольнике АВС точки Р и Е – середины сторон АВ и ВС соответственно, точки М и Н – середины отрезков АР и СЕ соответственно. Если РЕ =7 см, то отношение МН : АС равно

ОТВЕТ: 3:4
Диагональ АС и средняя линия MN трапеции ABCD пересекаются в точке К. Если AD = 24 см, ВС = 18 см, то отношение МК : МN равно
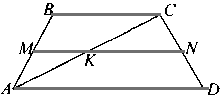
ОТВЕТ: 3:7
Если в трапеции ABCD (ВС и AD основания) ВН – высота, AD = 10 см, ВС = 6 см, АВ = 4 см и cosABH = 0,5, то площадь трапеции равна
ОТВЕТ: 16. |
|
|
 Скачать 116.91 Kb.
Скачать 116.91 Kb.


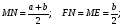
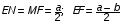

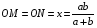 или
или 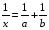

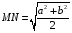

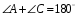

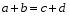

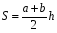
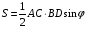

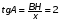 (тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету). Следовательно, x = 10/2 = 5.
(тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету). Следовательно, x = 10/2 = 5.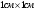 изображена трапеция. Найдите ее площадь в квадратных сантиметрах.
изображена трапеция. Найдите ее площадь в квадратных сантиметрах.
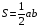 , где а и b – катеты прямоугольного треугольника.
, где а и b – катеты прямоугольного треугольника. 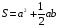 . Исходя из рисунка а=5 см., в=4 см. Следовательно,
. Исходя из рисунка а=5 см., в=4 см. Следовательно, 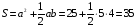 см.
см. 
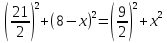
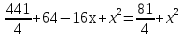
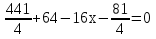
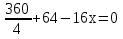
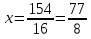
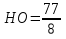
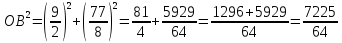
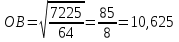
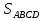

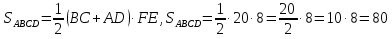
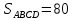 .
.
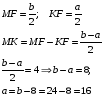


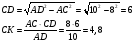
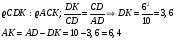
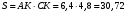

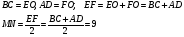

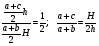

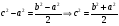
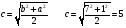

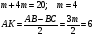
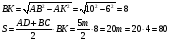

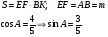
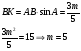

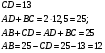
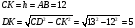
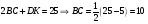
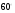 , а площадь равна
, а площадь равна 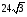 , вписана окружность. Найдите радиус этой окружности.
, вписана окружность. Найдите радиус этой окружности.
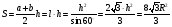
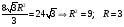
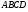 вписана в окружность. Найдите среднюю линию трапеции, если ее большее основание
вписана в окружность. Найдите среднюю линию трапеции, если ее большее основание 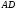 равно 15, синус угла
равно 15, синус угла 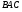 равен
равен 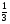 , синус угла
, синус угла 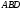 равен
равен 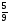 .
.
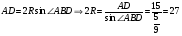
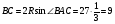
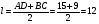
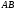 и
и 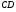 трапеции
трапеции 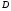 , если одно из оснований трапеции на 9 больше другого.
, если одно из оснований трапеции на 9 больше другого.
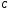 проведем прямую линию, параллельную стороне
проведем прямую линию, параллельную стороне