Урок- «карусель» в 7 классе по теме «Действия с одночленами и многочленами»
 Скачать 47.7 Kb. Скачать 47.7 Kb.
|
| Учитель математики МБОУ «СОШ № 143» г. Красноярска Князькина Татьяна Викторовна Урок- «карусель» в 7 классе по теме «Действия с одночленами и многочленами» Очень эффектным, интересным и продуктивным методом обучения является интерактивная "карусель". Это образовательная игра пригодна и для проведения урока, и для внеклассного мероприятия (например, олимпиада). Данный метод вовлекает всех учащихся в образовательную деятельность, даёт возможность коллективного поиска решения задач, обмена идеями, информацией, математическими знаниями. А, так как математическая "карусель"- это соревнование между группами, то урок в такой форме разжигает у детей не только спортивный азарт и волю к победе, но и мотивирует учащихся к получению более широких познаний в области математики. Данный урок является завершающим по теме. Класс делится на 4-5 групп по одинаковому количеству человек, для проверки ответов в качестве судей можно пригласить учеников из других классов. Столы в кабинете надо расставить в два ряда так, чтобы для каждой группы было предоставлено 2 стола: для игры на старте и игры на финише. В группе задачи решают сообща, судье предоставляется только ответ в письменном виде, чтобы игроки из других команд его не услышали. Методику оценивания можете разработать сами. Рекомендую самооценку и взаимооценку в группе. Правила математической "карусели". Математическая "карусель" – это командное соревнование по решению задач. Побеждает команда, набравшая наибольшее число очков. Задачи решаются на двух рубежах – исходном и зачётном. Всем членам команды присваиваются порядковые номера (на пример от 1 до 6). По сигналу команды на исходном рубеже начинают решать задачи и предъявляют решение (или ответ) судье. Если оно верное, игрок №1 переходит на зачётный рубеж и получает задачу там, а члены команды, оставшиеся на исходном рубеже получают новую задачу, если опять верный ответ, то игрок №2 переходит на зачётный рубеж и присоединяется к игроку № 1 и т.д. В дальнейшем члены команды, находящиеся на “исходном” и “зачётном” рубежах, решают новые задачи независимого друг от друга. Все игроки в команде как бы выстроены в очередь. Если на исходной позиции задача решена правильно, игроки в порядке очереди переходят на зачётный рубеж, но если на зачётном рубеже задача решена неправильно, то опять в порядке очереди игроки возвращаются на исходную позицию. И на исходном и на зачётном рубежах команда может в любой момент отказаться от решения задачи. При этом задача считается нерешённой. После того, как часть команды, находящаяся на каком – либо из двух рубежей рассказала решение очередной задачи или отказалась от неё, она получает новую задачу. На исходном рубеже за каждую верно решённую задачу ставится 1 балл, за первый верный ответ на зачёте команда получает 3 балла, за второй верный ответ 4 балла, и т.д. Если же очередная задача решена неверно, то цена следующей задачи зависит от цены нерешённой следующим образом. Если цена неверно решенной задачи была 6 баллов или больше, то следующая задача стоит 5 баллов. Если неверно решённая задача стоила 5 баллов, то следующая задача стоит 4 балла, если же неверно решённая задача стоила 3 или 4 балла, то следующая задача стоит 3 балла. Игра для команды заканчивается, если: а) кончилась игровое время, б) кончились задачи на зачётном рубеже, в) кончились задачи на исходном рубеже, а на зачётном рубеже нет ни одного игрока. Игра оканчивается, если она закончилась для всех команд. Побеждает команда, набравшая больше баллов. Продолжительность "карусели" может составлять от 20 минут до 2 часов и зависит от её целей, количества и трудности задач и размеров команд. Задания исходного рубежа (Старт)
0,5b·4b²-5b·0,3b-3b²·(-0,2b)+14b²·0,5-25b·0,3b²
Задания зачетного рубежа (финиш)
P₂=20x³+15x²y+4xy²-3y³; P₃=10x³-12x²y-5xy²+y³
а) подешевела, б) подорожала, в) осталась в прежней цене.
Ответы старта.
Ответы финиша.
|
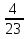
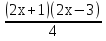 =x²-1
=x²-1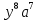
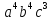
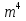 -25
-25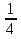 =0,25
=0,25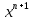 y-8
y-8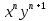
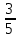 =0,6
=0,6