Реализация межпредметных связей на уроках математики
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
2.2. Средства развития познавательного интереса учащихся к математике в процессе реализации межпредметных связей Выявлять связь школьного курса математики с жизнью и другими учебными предметами всегда важно и интересно. Как сделать так, чтобы этот интерес не угас к концу обучения? Как добиться того, чтобы урок приносил радость и детям, и учителю? Для того, чтобы решить данную проблему, необходимо на уроках использовать методы активного обучения, это вносит непринужденную обстановку в урок, позволяя решать поставленные задачи. При проведении уроков можно использовать занимательную дидактику, сюжетно – ролевые и деловые игры межпредметного характера. Программа по географии 9 класса предусматривает изучение темы «Территориальная структура АПК». Закрепление материала можно провести в форме учебно-деловой игры «Фермер», предложенной В.М. Симоновым в своем учебном пособии [20], с целью закрепить материал по географии сельского хозяйства страны, а также с целью формирования вычислительных навыков и навыков анализа, работы со статистическими данными. Учащиеся исполняют роли арендаторов и фермеров. В процессе проводятся расчет количественно-качественных характеристик продукции; стоимость перевозок различной продукции; стоимость участков земли или их аренда; урожайность различных видов сельскохозяйственных культур. Сценарий игры: На доску вывешивается карта района, на территории которого будет разворачиваться игра. На карте указан город (потребитель) и три кольца зон, распределенных по секторам. Каждое из колец находится на разном расстоянии от города: первое –10 км, второе – 50 км, третье – 150 км. Сектора (продаваемые или сдаваемые в аренду участки земли) имеют разную площадь и разную цену. Предлагается возможным выращивание следующих сельскохозяйственных культур и тариф на перевозку продукции. Для производства 3 т молока на 1 корову требуется 25 к.е., которые можно получить с 5 га пастбищ, 5 т кормовых и 2,5 т зерна. Но зерно требуется предварительно отвезти в город и переработать по цене 50 руб. за 1 т. Спрос населения:
Игроки выбирают вид землевладения и на аукционе приобретают земельные участки под ссуду в банке (беспроцентный заем в размере 10 000 руб. Все остальные заемы даются под 5% годовых). Выбирается и объявляется вид сельскохозяйственной деятельности (цветоводство, животноводство и т.п.). Более одного вида в конкретный год выбирать нельзя. Деятельность ежегодно должна меняться. После обозначения всех хозяйств на карте каждый должен рассчитать свой годовой доход и заключить договор с потребителем. После заключения договоров извлекается карточка из конверта «Случайные события». Делается пересчет. После осуществления операций по выращиванию, переработке и продаже подсчитывается уровень удовлетворения платежеспособного спроса потребителей. Если спрос удовлетворен полностью, цена на данную продукцию на «следующий год» остается прежней. Если спрос не удовлетворен, то цена возрастает на величину неудовлетворенного спроса для «следующего года». (Например: спрос по молоку 100 тыс. руб., было продано на 80 тыс. руб., т.е. спрос удовлетворен на 80%. Следовательно, цена молока возрастает до 120 % от исходной). После проведения расчетов между всеми участниками игры и получения годовой прибыли (дохода) они принимают решения о видах деятельности на следующий год. Подводятся предварительные итоги. После завершения трехгодичного цикла производства, соответствующего максимальному севообороту, выводятся окончательные оценки. В завершение игры подводятся итоги – выявляются «миллионеры» и «банкроты». Модернизация российского образования предполагает расширение возможности интеграции предметов школьной программы. Наибольшие перспективы кроются в тесной взаимосвязи таких дисциплин, которые всесторонне рассматривают человека в философском единстве как существо биологическое и социальное. Именно сам человек, его взгляды на окружающий мир, его деятельность наиболее близки и понятны учащимся. Современный подход к объяснению истории человечества невозможно обосновать без знания географических и биологических особенностей развития; их, в свою очередь, нельзя объяснить, не зная основ химии и физики; а современные экологические, демографические, социально-экономические проблемы трудно понять в отрыве от истории и математики. Интеграцию этих предметов можно применять как на уроках, так и во внеурочное время. Одна из таких возможностей – проведение познавательных мероприятий игрового характера. Например, игра «Я знаю!» может проводиться в классах среднего и старшего звена в качестве закрепления изученного материала, повторения или организована как самостоятельное мероприятие во время проведения Недели естественно-математических и обществоведческих дисциплин в школе. Игра позволяет проверить знания по географии, биологии, математике, физике, дает возможность учащимся проявить находчивость, чувство юмора, творческую активность, развивает познавательный интерес, уважение к естественнонаучным дисциплинам, способствует укреплению классного коллектива на основе совместной деятельности и сопереживания за свою команду. Первый тур – «Проверим знания». Капитаны команд получают лист, где будут записывать ответы на вопросы ведущего. Ведущий задает командам вопросы по разным учебным дисциплинам, игрокам отводится по одной минуте для ответа на каждый вопрос.
–Монета, конечно, поддельная, – ответил собиратель. Как он узнал это, не видя ни самой монеты, ни даже ее изображения?
Второй тур – «Покажем знания». Капитаны поочередно подходят к столику жюри и выбирают карточки с номерами вопросов. Синий цвет карточки предполагает задание из области географии, зеленый – биологии, красный – математики, белый – физики. География:
Биология:
Физика:
рис.4 М    атематика: атематика:+ + = -5
Третий тур – «Удивим знаниями». Командам необходимо раньше соперников дать правильный ответ на вопрос ведущего. Капитан поднятой рукой извещает о готовности команды отвечать.
Р 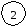 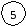 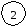 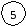 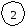 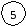 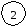 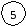 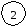 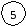 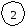 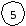 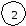 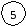 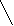   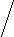 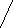    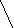 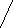 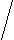 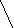 ешение: ешение:
В конце игры подводятся итоги, награждение победившей команды. Подводится также награждение в номинациях: «Лучшая команда», «Лучший игрок». Тема «Алгоритмизация и программирование» изучается на всех ступенях средней школы, но на разном уровне. В начальной школе происходит знакомство на интуитивном уровне с понятиями алгоритма, алгоритмических конструкций, основ алгебры логики. В качестве учебных задач рассматривают бытовые, игровые, сказочные алгоритмы. В средних классах школы в рамках данной темы происходит уточнение понятия алгоритма, основы алгебры логики излагаются на более формальном уровне. И.Н. Фалина в своей работе [24] пишет, что понятие алгоритма является фундаментальным понятием математики и информатики. Первоначально под словом алгоритм понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи. В целях развития познавательного интереса учащихся к данной теме А.А. Чернов в своем учебном пособии [25] предложил задания межпредметного содержания:
Условие существования треугольника известно из геометрии: сумма двух любых сторон должна быть больше третьей. Программа может выглядеть следующим образом: Program v1; Var a, b, c: real; Begin Writeln ('введите длины трех сторон треугольника'); Readln (a, b, c); If (a+b>c) and (b+c>a) and (a+c>b) Then writeln ('треугольник существует') Else writeln ('треугольник не существует'); End. Связи между науками математики и физики многообразны и постоянны. Математика как наука сформировалась первой, но по мере развития физических знаний математические методы находили все большее применение в физических исследованиях. Взаимосвязи математики и физики определяются, прежде всего, наличием общей предметной области, изучаемой ими, хотя и с различных точек зрения. Взаимосвязь математики и физики выражается во взаимодействии их идей и методов. Эти связи можно условно разделить на три вида: – физика ставит задачи и создает необходимые для решения математические идеи и методы, которые в дальнейшем служат базой для развития математической теории; – развитая математическая теория с ее идеями и математическим аппаратом используется для анализа физических явлений, что часто приводит к новой физической теории, которая в свою очередь приводит к развитию физической картины мира и возникновению новых физических проблем; – развитие физической теории опирается на имеющийся определенный математический аппарат, но последний совершенствуется и развивается по мере его использования в физике. В курсе физики 9 класса вывод формулы перемещения при равноускоренном движении основывается на формуле площади трапеции, которая учащимся к тому времени неизвестна. Изучение площадей отнесено к концу курса геометрии 9 класса. Учащимся можно предложить получить данную формулу, используя те сведения, которые им уже известны: – формула площади прямоугольника; – диагональ прямоугольника делит его на два равных треугольника. SOABC = SOADC + SABD = SOADC + Sx = U0x *t + 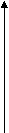   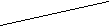 Е В Е В  А D А DU0x U0x  О С О СОсознание учащимися того факта, что они нашли выход из трудного положения, что решили задачу по-своему, заставляет их гордиться собой, своими знаниями, побуждает интерес к изучаемым предметам. Вместе с тем, данный пример позволяет показать, что математика – это факел, освещающий путь всем другим наукам. Повторение и обобщение знаний о величинах (скорость, время, путь, площадь, объем), формулах, их выражающих, отработку умений их применения можно провести в форме игры-конкурса, целью которого будет подчеркивание взаимосвязи физики и математики; развитие логического мышления; воспитание познавательного интереса к учебным предметам. Мы приведем лишь некоторые вопросы и задачи по физике и математике, которые можно использовать в качестве заданий в ходе игры.
Мы считаем, что задачи такого содержания, воспитывающие познавательную активность, будут интересны для учащихся. Интересен урок-ярмарка «Старинные русские меры», который можно провести, преследуя следующие цели:
Оборудование урока: Таблицы старинных мер
Учитель объявляет тему и цель урока. Рассказывает, что такое ярмарка прошлого века. Стук в дверь (входят купцы и три дочери первого купца). Купцы (вместе): Здравствуйте, добры молодцы и красны девицы! 1-й купец: Сегодня мы проводим в вашей губернии ярмарку. Приглашаем вас приобрести наш товар. Товару разного много, покупайте, не скупитесь. Покажите смекалку, сообразительность, умение считать, быстроту мышления. 2-й купец: Будет куплен весь товар, получите награду по заслугам. Учитель: Но, простите, уважаемые купцы! Как же добры молодцы и красны девицы будут покупать товар, ведь они из разных поместий, учились мало, не знают ни мер длины, ни денежных единиц. 1-й купец: А помогут им волшебные таблицы и мои дочери, которые получили хорошее домашнее образование. Учитель: Ребята, эти таблицы помогут вам перевести старинные единицы мер в метрическую систему мер. Выступают дочери купца, рассказывая о старинных мерах веса, длины и старинных деньгах, поясняя таблицы. Учитель: Какая же ярмарка без шутки, веселья, песен. Группа учащихся исполняет русскую народную песню. 1-й торговец: Добры молодцы, красны девицы, Вы на ярмарку пришли, Много денег принесли, Вы нам деньги принесли, А мы товару припасли. Покупая наш товар, знай: Там задача ждет тебя, Да! Учитель: Ребята, покупая товар, вы должны перевести старинные деньги в копейки, пользуясь таблицей. Откройте тетрадь, запишите число. Решать можно индивидуально и группой. За решение задачи получите жетон. 2-й торговец: Продается зоосад: 2 цыпленка, 5 гусят. 1-й купец: В нашем краю, словно в раю: Рябину, грибы корзиной бери… Кладу на весы 2 фунта еды. Покупай ягоды, За фунт плати полтину. 3-й торговец: Продается модный жилет. Модный жилет с поношенным пиджаком стоит полтора рубля с пятиалтынным. Пиджак стоит рубль с пятиалтынным. Сколько стоит жилет? 4-й торговец: Продается чебак на золотой цепочке. 1 фунт чебака стоит 4 гривенника, за цепочку золотую заплатить надо 5 рублей с пятиалтынным. Сколько стоит весь товар? 2-й торговец: Продаются в лесопарке два мышонка, два крота. Налетай, покупай! 1-торговец: Капуста не пуста, сама летит в уста. Ты приготовил деньги на покупку кочана в 3 кг? 1 кг капусты стоит полтину. 1-й торговец: На прилавке остался лишь кочан массой 5 кг, да и цена 1 кг выше на алтын с 4 грошами. Придется тебе купить этот кочан! 3-й торговец: Папаха боярская с сапогами изношенными, вместе стоят без четырех грошей 6 рублей с полтиной. Покупай. Могу обмен устроить: за папаху давай 15 лаптей, а за сапоги 3. 4-й торговец: Продается курица 3 фунта весом, несущая яички не простые, а золотые. Сом в 2 фунта, не простой – ученый. 1 фунт сома стоит рубль с двумя гривенниками. 1 фунт курицы стоит рубль с полтиной без двух грошей. 2-й торговец: в бочонке 32 фунта огурцов. Полбочонка продаю по 4 гривенника с двумя грошами за фунт, а другую половину – по полтине за фунт. 3-й торговец: Продаю хвост лисий. Отдам за две полтины с пятиалтынным или за два хвоста куницы с полушкой. Покупай лисий хвост. 4-й торговец: Продаю налим и щуку. Один фунт налима стоит полтину с четырьмя алтынами, а щука – 2 рубля без гривенника. Налим весит 4 фунта, а щука – 2 фунта. 2-й торговец: Дневной рацион для поросенка: картофель – 10 фунтов, свекла – 2 фунта. Закупай овощей на три дня, если два фунта картофеля стоят гривенник, а фунт свеклы – алтын. Все торговцы: Товар продан. Ярмарка закрывается 2-й купец: Да, умны вы, красны девицы и добры молодцы. Думаю, ваш учитель вознаградит вас сполна, по заслугам. Учитель: Итак, ребята, где вы побывали? Каковы особенности русской ярмарки? Как вы думаете, удобна ли старинная система мер? Когда был осуществлен переход от старинных систем мер к современной метрической системе мер? Учитель выставляет оценки, комментируя их. Подводятся итоги урока. Как показывают исследования и практика работы, у учащихся различных возрастных групп наблюдаются различия в мотивации обучения. В младшем звене основным мотивом является новый вид деятельности человека, его изменившийся статус в обществе. В старшем звене основополагающим мотивом является профессиональная направленность – выбор «кем быть?» Но в среднем звене наблюдается «вакуум мотивации». Средством наполнения этого «вакуума мотивации» является возбуждение интереса к предмету. |
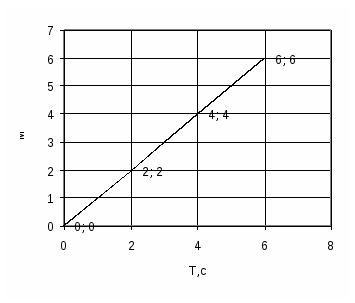
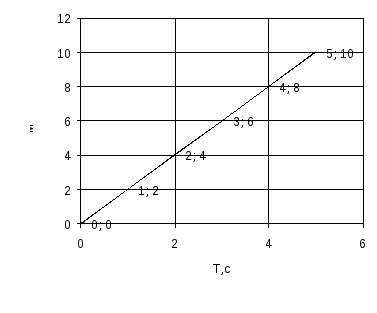 о графикам зависимости путей от времени двух тел, движущихся равномерно, определите скорости этих тел (рис. 4). Скорость какого тела больше.
о графикам зависимости путей от времени двух тел, движущихся равномерно, определите скорости этих тел (рис. 4). Скорость какого тела больше.