Реализация межпредметных связей на уроках математики
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
2.3. Организация и результаты педагогического эксперимента Разработанная в данном исследовании методика развития познавательного интереса в процессе реализации межпредметных связей проходила экспериментальную проверку в МОУ Береговая СОШ в период с 1 января 2007 года по 1 февраля 2008 года, которая состояла из трех этапов:
Задачи поискового эксперимента: 1. В процессе анализа учебной литературы выявить роль межпредметных связей в развитии познавательного интереса на уроках математики. 2. Определить содержание теоретического межпредметного материала в школьных учебниках, а также группу задач, которую можно предложить учащимся на уроках межпредметного содержания с целью развития познавательного интереса. В ходе анализа литературы и школьной документации, в результате наблюдения, анкетирования учащихся выявлены проблемы, решение которых привело к идее использования межпредметных связей на уроках математики с целью привития интереса к предмету. В результате анкетирования, изучения школьной документации установлено, что у всех учащихся резко падает интерес к предмету на рубеже 8 – 9-го классов. Заметно снижается качество знаний, о чем свидетельствуют результаты итоговых работ по алгебре и геометрии в конце учебного года (см. приложения 3,4). По результатам анкетирования учебный процесс в целом не представляет интереса для большинства учащихся, среди них есть и такие, которые обучаются по принуждению (диаграмма 1). Диаграмма 1 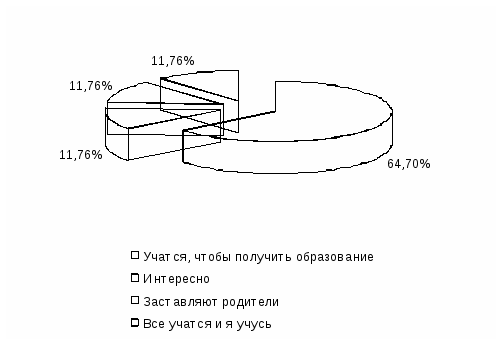 Результат тестирования, определяющий отношение учащихся к учебному процессу. Учащиеся подросткового возраста, а тем более слабоуспевающие из них, особенно быстро устают от длительной, однообразной умственной работы. Усталость – одна из причин падения внимания и интереса к учению. Анализ аттестационных работ выпускников свидетельствует о том, что знания некоторых учащихся по математике поверхностны, фрагментарны, непрочны. Учащиеся класса не умеют выполнять операции над обыкновенными и десятичными дробями, не умеют строить и анализировать графики линейной и квадратичной функций. Разумеется, было бы неверно утверждать, что все учащиеся так плохо подготовлены. Но, к сожалению, учащиеся, обладающие добросовестными знаниями, составляют от общего их числа весьма невысокий процент. В процессе диагностики было проведено анкетирование, выявляющее отношение учащихся к учебным предметам. Из 34 опрошенных математикой увлечены только 8 учащихся. Результаты анкетирования представлены в приложении (см. приложение 5). Таким образом, было установлено, что проблема падения интереса к математике является актуальной. Организовать процесс развития интереса возможно с привлечением в организацию урока задач, теоретических сведений межпредметного содержания, а также с проведением интегрированных уроков, уроков-турниров, игр, КВН и т.д. Целью второго этапа эксперимента являлась проверка эффективности применения задач межпредметного содержания и интегрированных уроков как средства развития познавательного интереса на уроках математики. Обучающий эксперимент проходил в 7 классе, в котором приняли участие 16 человек. За два года обучения в среднем звене успеваемость учащихся резко снизилась, понизился интерес к школьным предметам, в том числе и к математике, несмотря на то, что в начале пятого класса многие выделяли математику как один из самых интересных предметов школьного курса. Об этом свидетельствуют результаты анкетирования «Изучение интереса учащихся к школьным предметам» ( см.приложение 5). Диаграмма 2 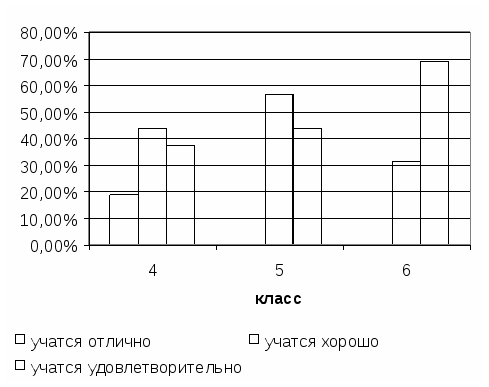 Результаты исследования успеваемости класса за три года. Проблема падения интереса учащихся класса волнует коллектив учителей нашей школы. Большая часть учащихся может заниматься на «4» и «5». Для того, чтобы выяснить причины сложившейся ситуации, был предложен тест «Диагностика уровня школьной тревожности» (методика Филлипса) [2]. Цель методики состоит в изучении уровня и характера тревожности, связанной со школой у детей среднего школьного возраста. Тест состоял из 58 вопросов, которые предлагались в письменном виде. На каждый вопрос требовалось однозначно ответить «Да» или «Нет». Результаты тестирования приведены в таблице 2. Число несовпадений по каждому измерению для всего класса составляет 35%. Можно говорить о том, что уровень тревожности в классе средний. Таблица 2
Диагностика уровня школьной тревожности. Анализ результатов показывает, что большая часть учащихся класса испытывает негативные эмоциональные переживания, сопряженные с необходимостью самораскрытия, предъявления себя другим, демонстрации своих возможностей. Также у некоторых учащихся наблюдается негативное отношение и переживание тревоги в ситуациях проверки знаний, достижений, возможностей; проблемы и страхи в отношениях с учителями. Чтобы пробудить интерес учащихся к учению учителям, работающим в 7 классе, было рекомендовано разнообразить формы проведения уроков через внедрение в учебный процесс материалов межпредметного содержания, как средства, способствующего развитию познавательной активности. Первая глава, с которой начинается курс «Алгебра – 7» это «Алгебраические выражения», в начале изучения которой несколько часов отводится на повторение темы «Числовые выражения». В ходе изучения данного учебного материала, на каждом уроке использовались задания с интересными историями, которые заканчивались вопросом и математическим упражнением, решая которое и получая ответы, ученик мог ответить на вопрос. Кроме того, формулировки заданий позволяли расширить кругозор, пробуждали любопытство, любопытство, как известно, переходит в любознательность, и просыпается интерес к предмету. Примеры таких заданий: В старину корой этого дерева «заговаривали» зубы и лихорадку. Вырежут из коры этого дерева треугольник, чтобы отдать дань Богу Отцу, Богу Сыну, святому духу, и трут десны, читая молитву. А потом треугольник прикладывают на место, откуда его вырезали. Боль утихает. И неведомо было людям, что дело не в богах, а в содержащихся веществах в коре именно этого дерева. О каком дереве идет речь? 614: 760 – 57 * 13 + 204476 : 68 809 – И, 89 – Е, 751 – Б, 741 – С, 3007 – А, 307 – Р, 37 – З, 3748 – Т, 68 – Н, 168 – П, 3075 – О, 8009 – Л, 71 – Ь. Ответ: осина. Соком этого растения был отравлен король датский, отец Гамлета. Сейчас оно входит в состав мазей для лечения радикулита, так как обладает обезболивающим свойством. Что это за растение? 227,36 : (865,6 – 20,8 * 40,5) * 8,38 + 1,12 – 44. 842,4 – А, 844,2 – К,23,2 – У, 93,5 – С, 9,8 – М, 84,24 – О, 82, 124 – Н, 83,244 –Д, 39,244 – Р. В таких заданиях даются ответы с лишними буквами, соответствующие ошибкам, которые может допустить ученик. Задания могут выполняться всем классом, группой учащихся или индивидуально. Можно дать их на любом этапе урока. Тематика таких заданий может быть разнообразна, например: «Мир растений», «Мир животных», «Живопись», «История математики» и др. В домашних заданиях присутствовали элементы творчества: учащимся предлагалось самим составить аналогичные задания, был объявлен конкурс рисунков, изображенных с помощью только цифр или геометрических фигур. Особую активность проявляли слабоуспевающие учащиеся. Т.П. Григорьева в своем учебном пособии [8] предложила разработку урока «В поход за знаниями», проведение которого помогает расширить знания о природе родного края, повторить и применить знания по темам «Пропорция», «Равнобедренный треугольник». В начале путешествия можно провести устную разминку.
Контроль знаний: Треугольник называется равнобедренным, если:
В равнобедренном треугольнике углы при основании:
Углы при основании равнобедренного прямоугольного треугольника равны:
Один из углов равнобедренного треугольника в два раза больше другого. Найдите углы равнобедренного треугольника:
Найдите неизвестные члены пропорции: х:
Далее учитель рассказывает учащимся легенду: Усталый северный чужеземец пришел в страну Великиго Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараонов, что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы. – Кто ты? – спросил верховой жрец. – Зовут меня Фалес. Родом я из Милета. – Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? Жрецы согнулись от хохота. – Будет хорошо, – насмешливо продолжал жрец, – если ты ошибешься не более чем на сто локтей! – Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. – Хорошо, – сказал фараон, – Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим Ваше искусство. Греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Фараон и жрецы, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадавшего по тени высоту огромного сооружения. Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна тоже равняться длине отбрасываемой ею тени. Задача греческого мудреца представляется нам детски просто, но не будем забывать, что смотрим мы на нее с высоты грандиозного здания геометрии, воздвигнутого уже после Фалеса. За 300 лет до нашей эры греческий математик Евклид написал замечательную книгу, по которой обучались геометрии в течение двух тысячелетий после его смерти. Заключенные в ней истины, известные теперь каждому школьнику, не были еще открыты в эпоху Фалеса. А чтобы воспользоваться тенью для решения задач о высоте пирамиды, надо было знать уже некоторые свойства треугольника (первое из которых открыл сам Фалес): 1. Углы при основании равнобедренного треугольника равны. И обратно – что стороны, лежащие против равных углов треугольника, равны между собой; 2. Сумма углов всякого треугольника равна двум прямым углам. Только вооруженный этими знаниями Фалес вправе был заключить, что когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды, центр ее основания и конец ее тени должен обозначать равнобедренный треугольник. Этим простым способом очень удобно, казалось бы, пользоваться в ясный день для измерения высоты одиноко стоящих деревьев, тень которых не сливается с тенью соседних. Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равные высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде применим не всегда. Нетрудно, однако, изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Измерив, кроме того, и свою тень или тень какого-нибудь шеста, вы можете вычислить искомую из пропорции: AB : ab = BC : bc, так как высота дерева во столько же раз больше вашей собственной высоты (или высоты шеста), во сколько раз тень дерева длиннее вашей. Далее можно рассказать, как измерить высоту дерева без помощи теней. Для этого необходимо воспользоваться свойством равнобедренного прямоугольного треугольника, обратившись к услугам прибора, который легко изготовить из дощечки и трех булавок (см. приложение 6). После этого можно перейти к измерению ширины реки с помощью этого же прибора, а также проверить результат способом «козырька», который заключается в следующем. Надо стать лицом к реке, надвинуть фуражку на глаза, чтобы нижний обрез козырька точно совпал с линией противоположного берега. Козырек можно заменить ладонью, записной книжкой. Затем, не изменяя положения руки, повернуться налево или направо и заметить самую дальнюю точку, видимую из-под козырька (ладони, записной книжки). Расстояние до этой точки и будет примерно равно ширине реки (см. приложение 7). В конце урока предложить учащимся измерить ширину реки двумя способами, высоту дерева двумя способами, предложить свой способ измерения высоты дерева. В ходе урока заслушать сообщения учащихся о реках Амурской области, «Охрана окружающей среды», «Лес – легкие Земли». Такой урок, позволяет воспитывать элементы экологической культуры, интерес по улучшению окружающей среды, воспитывает любовь к математике, развивает элементы логического мышления, творческой деятельности. На уроках алгебры учащиеся знакомятся с формулой средней скорости. В учебнике рассматривается достаточное количество задач на движение. На уроках физики вводятся понятия: механическое движение, скорость, как важнейшая характеристика механического движения, траектория, пройденный путь. В целях развития навыков решения задач на одном из уроков можно предложить задачу следующего содержания:
Перед выполнением задания целесообразно будет повторить следующие понятия:
В домашнее задание можно включить задачу: Расстояние от Берегового до Зеи по прямой 75 км. Расстояние между этими населенными пунктами по карте Амурской области – 5 см. Найдите масштаб карты. С целью воспитания познавательного интереса к предмету, систематизировать умение учащихся применять формулы сокращенного умножения и развивать вычислительные навыки, урок-повторение формул сокращенного умножения можно провести в виде игры «Путешествие по пустыням мира». В ходе игры, выполняя задания, учащиеся отвечают на вопросы. О пустыне Гоби говорят, что у нее 33 лица, и все они разные. Сильнейшие ураганные ветры вызывают песчаные бури, которые за долгие века, словно резец умелого скульптора, придали местным камням причудливые формы. Где же находится эта пустыня? Представьте в виде многочлена. Ответы:
25а2 +4в2 (Р) (Получится Монголия). Ученики решают у себя в тетрадях, когда получают ответ, по карте находят Монголию и показывают пустыню Гоби. Пример следующего задания: Узкой полоской тянется вдоль Атлантического побережья юга Африки самая холодная и безводная пустыня Намиб – гиблое место, известное как… Учащимся предлагается разложить многочлены на множители. После выполнения задания ученики дают правильный ответ. Подобных заданий можно придумать очень много, мы привели для примера только часть из них.
(Ответ: Берег скелетов). Каждый учитель в процессе своей деятельности ставит не только общеобразовательные, но и воспитательные задачи:
Для решения воспитательных задач, мы предлагаем использовать экскурсии. Учебным планом школы не предусмотрены производственные экскурсии собственно по математике, но учитель математики может проводить их совместно с учителями других дисциплин. Такие экскурсии обычно называют комплексными. Собранные во время экскурсии материалы можно оформить в виде таблиц, схем, стендов. Отдельные задания, оформленные в виде докладов, выставляются в кабинете математики, становясь достоянием всех учащихся. Объектами экскурсии учащихся 7 класса могут служить строительная площадка, башенный кран. Цель экскурсии – рассмотреть простые механизмы, используемые в строительстве: рычаг, блоки, лебедки. Установить, какие физические величины являются обратно пропорциональными. Сделать необходимые измерения для составления задач на вычисление силы, требующейся для поднятия тел данной массы с помощью рычага. Экскурсии помогают натолкнуть учащихся на более сознательный выбор своей будущей профессии, а также делают урок математики необычным, интересным, а это как раз то, к чему мы стремимся. С записью чисел в стандартном виде учащиеся встречаются не только на уроках математики, но и на физике, географии. В качестве домашнего задания учащимся было предложено привести примеры, где для записи больших чисел применяются степени числа 10. С этой частью домашней работы справились все, некоторые учащиеся приготовили небольшие сообщения. Приведем несколько примеров:
В ходе данного этапа с целью проверки качества усвоения изученного материала, а также эффективности методики на уроках проводились контрольные работы, результаты которых представлены в приложении (см. приложение 8).
Геометрия – новый предмет, к изучению которого учащиеся приступили в этом учебном году. Сравнительный анализ уровня овладения знаниями, умениями и навыками представлен на диаграмме 3. Диаграмма 3 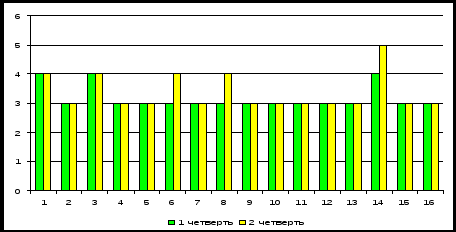 Анализ итоговых оценок по геометрии за 1 и 2 четверти. В конце эксперимента учащимся было предложено ответить на вопросы анкеты, выявляющей интерес к учебным предметам. В конце первого полугодия был проведен контрольный срез знаний «Проверка вычислительных навыков», аналогичный тому, который был дан учащимся в начале эксперимента. Сравнительный анализ результатов анкетирования и контрольных срезов до и после эксперимента по каждому ученику представлены на диаграммах 4, 5.
Диаграмма 4 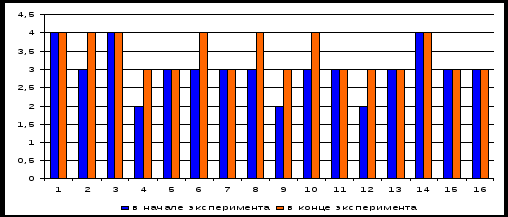 Сравнительный анализ контрольных срезов по каждому ученику. Диаграмма 5 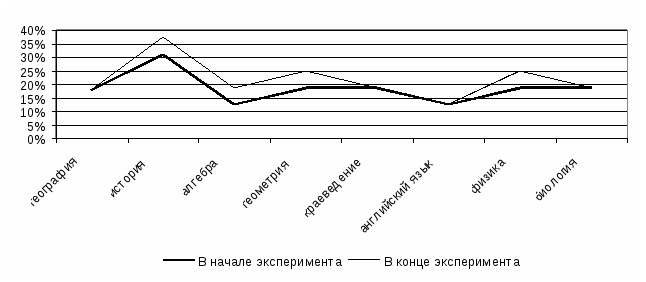 Сравнительный анализ результатов анкетирования, выявляющее отношение учащихся к учебным предметам до и после эксперимента. Таким образом, эксперимент подтвердил наше предположение о том, что применение качественных и количественных задач межпредметного содержания способствует развитию познавательного интереса учащихся. Разумеется, за столь короткий срок невозможно достичь значительных результатов, но наше предположение подтверждает уже состоявшийся факт: С 1996 / 97 учебного года в Береговой школе учителем А.Г. Троценко был проведен эксперимент, суть которого состояла в следующем. Одним учителем, начиная с 7 класса, велись уроки физики, математики (в дальнейшем и информатики), что позволило в полной мере осуществлять межпредметные связи этих, наиболее родственных между собой предметов. В десятом классе из параллели (по желанию учащихся) был создан класс с расширенным преподаванием математики и физики, для чего в учебном плане были выделены дополнительно по 1 недельному часу на эти предметы. Наблюдался неподдельный интерес к учебе у учащихся, в первую очередь к математике и физике. По окончанию школы одна ученица получила золотую медаль. Из 18 выпускников 14 поступили в ВУЗы, 4 – в Сузы. Только одна ученица поступила на коммерческой основе. Из них 15 человек поступили в учебные заведения, где профилирующими являются математика, физика или то и другое вместе. Итак, нами проведен анализ психолого-педагогической и научно-методической литературы по проблеме реализации межпредметных связей в процессе обучения математике учащихся основной школы. В процессе анализа методической литературы выявлены цели, которые преследует осуществление связи курса математики с учебными предметами; установлены типы связей между математикой и другими учебными предметами. Предложены способы привлечения межпредметного опорного материала в процессе сообщения новых знаний; выявлены приёмы повторения нового материала. Предложены средства, направленные на развитие познавательного интереса учащихся к математике в процессе реализации межпредметных связей, к которым относятся: занимательная дидактика, конкурсы, сюжетно-ролевые и деловые игры межпредметного характера, задания межпредметного содержания, познавательные мероприятия. |