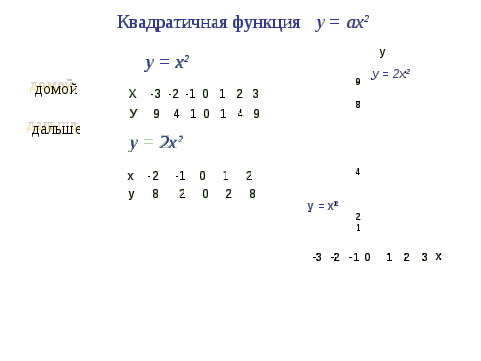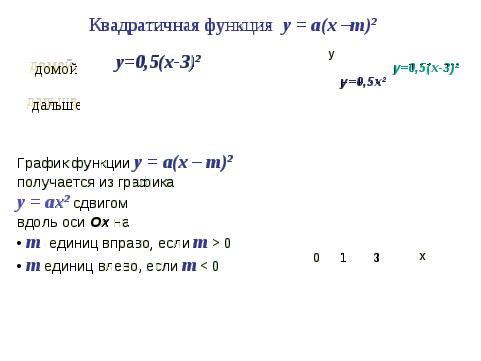Этапы урока
|
Задачи
|
Деятельность учителя
|
Планируемая деятельность учащихся
|
Методический комментарий
|
Орг. момент.
|
Подготовка учащихся к уроку.
|
Объявляет о начале урока, предлагает учащимся занять свои места.
|
Занимают свои рабочие места.
|
Важно задать высокий темп урока, чётко формулируя требования учащимся.
|
Проверка домашнего задания.
|
Выяснить, как учащиеся справились с выполнением домашнего задания.
|
Проецирует на экран отсканированное решение, выполненное одним из учащихся
|
Проверяют правильность решения задачи по предложенному образцу. Называют причины затруднений.
|
Сканирование желательно сделать перед началом урока.
Возможные затруднения при выполнении задания:
при нахождении ординат точек пересечения;
при построении графиков заданных функций.
|
Актуализация опорных знаний.
|
Подготовка учащихся к усвоению нового материала. Организация познавательной деятельности учащихся.
|
Проводит вводную беседу примерно следующего содержания: «С одним из видов квадратичной функции вы знакомы - это функция у = ах2.
Сегодня мы снова рассмотрим квадратичную функцию, но заданную уже в виде у = aх²+bx+c. А как вы, ребята, думаете, почему квадратичной функции нужно уделить особое внимание?»
Вопрос:
Как с помощью графика у=х2 построить:
а) у=2х2; б) у= ½ х2;
в) у= -2х2?
Вопрос:
Смогли бы вы построить график функции у=ах2+bx+c, если коэффициенты а,b,с будут заданы?
Как вы думаете, какую из известных вам кривых напомнит построенный график?
|
Участвуют в беседе.
Предполагаемые ответы:
1. Многие величины из окружающей нас жизни связаны зависимостью у = х2, например, площадь квадрата от его стороны.
2. Отражающая поверхность фары в автомобиле имеет параболическую форму.
3. Некоторые законы физики описываются квадратичной функцией.
Предполагаемые ответы:
График функции у = af(x) можно получить из графика функции у = f(х) с помощью растяжения от оси х в а раз, если а > 1, и с помощью сжатия к оси х в 1/а раз, если 0 < а < 1.
График функции у = -f(x) можно получить из графика функции у=f(х) с помощью симметрии относительно оси х.
Предполагаемый ответ:
Да, если взять достаточно большое количество точек.
Параболу.
|
Необходимо попросить учащихся привести примеры,
Слова учителя сопровождаются презентацией.
Слайд № 5

Слайд № 6

Слайд № 7
|
Создание проблемной ситуации.
|
Формирование навыков анализировать задачу на необходимость и достаточность данных для ее решения.
Воспитание культуры коллективной работы.
|
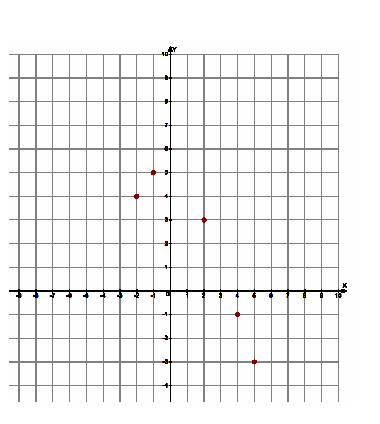
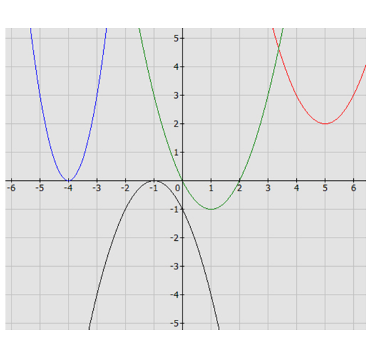
1. На координатной плоскости отмечены несколько точек. Постройте по этим точкам параболу.
2. Посмотрите внимательно на доску. Попробуйте установить соответствие между видом функции и видом графика.
у = (х-5)2+2,
у = 2х2+8х+32,
у = (х-1)2-1,
у = -(х+1)2.
Запишите на листе все проблемы, которые возникают при исследовании зависимости между формой, расположением параболы и функцией, ее задающей.
|
1. Учащиеся пытаются построить параболы по указанным точкам, но понимают, что задание могут выполнить лишь наугад, так как не хватает знаний и умений.
2. Предполагаемые проблемы, которые ставят учащиеся:
1. От чего зависит расположение вершины параболы?
2. Что может влиять на «ширину» параболы?
3. В каких случаях парабола пересекает ось абсцисс, касается ее или не пересекает?
4. Сколько достаточно знать точек, чтобы построить график любой квадратичной функции?
|
Работа в малых группах: получают раздаточный материал в виде листов, на которых изображена координатная плоскость с пятью отмеченными точками.
|
Организационно-деятельност
ный:
исследовательская работа;
определение темы урока;
свойства функции
у = a х²+ n;
у =а(х-т)2.
.
|
Обозначить тему урока.
Способствовать развитию математической речи, умению делать вывод через анализ рассматриваемой ситуации.
|
Проведем исследование функции у=ах2+bх+с.
Пусть b=0.
Рассмотрим функцию у=2х2-3.
Сравним таблицы значений для функций у=2х2 и у=2х2-3.
Учитель предлагает учащимся ответить на вопросы, записанные на доске.
Учитель предлагает учащимся построить график функции у=х2+2.
|
Учащиеся заполняют таблицы, сравнивают полученные значения и делают вывод, что график второй функции есть также парабола, полученная переносом графика первой функции вниз
параллельно оси ординат на 3 единицы.
Учащиеся отвечают на вопросы, сравнивают свойства функций и делают вывод.
Учащиеся строят график функции.
|
Учитель демонстрирует параллельный перенос.

Слайд № 8
Вопросы:
Область определения функции.
Область значений функции.
Указать промежутки возрастания и убывания функции.
Какая прямая является осью симметрии функции?
Чему равно наименьшее значение функции?
|
|
Рассмотрим функцию
у=0,5(х-3)². Для этого в одной системе координат построим графики функций
у= 0,5х2 , у=0,5(х-3)².
|
Учащиеся отвечают на вопросы, сравнивают свойства функций и делают вывод.
|
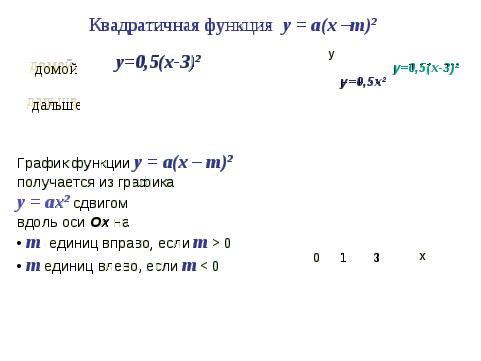
Слайд № 9
|
|
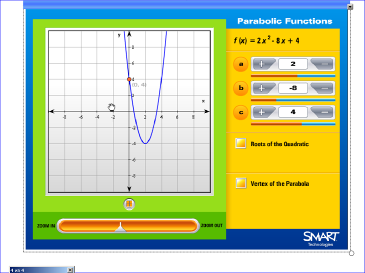
Учитель предлагает учащимся построить графики функций, пользуясь методом выделения полного квадрата.
у=х2+2х+4=(х+1)2+3
у=2х2-8х+4=2(х-2)2-4
|
Учащиеся по очереди выполняют построения на интерактивной доске.
|
Используется Macromedia Flash из коллекции Smart Notebook.
|
|
|
Учитель предлагает учащимся сделать вывод как построить график функции, используя метод выделения полного квадрата.
|
Учащиеся записывают в тетради формулы координат вершины параболы.
|
Вывод:
параболу у = aх² + bx + c = а(х – х0 )² +у0 можно получить сдвигом параболы у = aх² вдоль координатных осей.
|
Валеологическая пауза
|
Проводится гимнастика для улучшения мозгового кровообращения.
|
Проводит валеологическую паузу – 2 мин.
|
Выполняют упражнения по команде учителя.
|
Исходное положение – сидя на стуле, руки на пояс.
Упражнение №1.Голову наклонить вправо. И. п. Голову наклонить влево. И. п. (Упражнение повторяется 6 раз). Упражнение №2. Голову повернуть направо. И.п. Голову повернуть налево. И. п. (Упражнение повторяется 6 раз). Упражнение №3. Правая рука – вперёд, левая – вверх. И. п. Левая рука – вперёд, правая – вверх. И. п. (Упражнение повторяется 6 раз).
|
Закрепления изученного материала.
|
Проверка первичного уровня усвоения материала урока.
|
Учитель координирует действия учащихся, помогает проговаривать и обосновывать выполняемые преобразования
|
Часть учащихся выполняют преобразования на компьютерах, используя Macromedia Flash из коллекции Smart Notebook.. Остальные выполняют в тетрадях с помощью шаблонов, розданных учителем.
|
№ 617 (1, 3, 5).
Дополнительные тренировочные задания записаны на доске (для тех, кто быстрее справится с обязательным заданием).
|
Формировать умения устанавливать соответствие
между видом функции
и видом графика
|
Учитель консультирует тех учащихся, которые затрудняются при выполнении задания.
|
Учащиеся интерактивно устанавливают соответствие
между видом функции и графиком.
|
Тренажер развивает графические представления учащихся, позволяет им установить соответствие между видом функции и видом графика.

|
Итог урока.
|
Выяснить самооценку знаний учащимися.
|
Подводит итог урока, оценивает деятельность класса в целом и каждого учащегося в отдельности, выделяя удавшиеся моменты.
|
Выслушивают комментарии учителя, высказывают свою оценку деятельности на уроке, определяют свой уровень усвоения материала.
|
Достигли ли Вы сегодня поставленных целей?
Как ты оцениваешь свои знания, полученные сегодня (глубокие, осознанные, предстоит осознать, неосознанные)?
Что вызвало наибольшую трудность? Какие цели поставишь перед собой (в плане приобретения навыков)?
|
Домашнее задание.
|
Предоставить возможность каждому учащемуся проверить при выполнении дом. работы степень усвоения материала, отработать приёмы; желающим – реализовать свои возможности через выполнение дополнительного задания.
|
Учитель обращается к учащимися с просьбой проговорить изученные правила построения графиков. Знакомит учащихся с объёмом домашнего задания, комментируя его.
|
Учащиеся проговаривают основные правила преобразований графиков и записывают домашнее задание.
|
Обязательная часть д/з:
1. Прочитать п.38, просмотреть записи в тетради.
2. Выполнить № 609, № 617 (2, 4)
Желающим:
№ 616
|
 Скачать 104.67 Kb.
Скачать 104.67 Kb.