Обобщение по теме «Показательная, степенная, логарифмическая функции. Решение задач»
 Скачать 36.44 Kb. Скачать 36.44 Kb.
|
| Тема: Обобщение по теме «Показательная , степенная , логарифмическая функции . Решение задач». Цели:
. Оборудование : стенды с формулами, карточки и фишки, мультимедийный проектор, интерактивная доска, компьютер Тип урока: урок решения задач ХОД УРОКА . I .Орг. момент . II. Постановка цели . Добрый день, дорогие друзья ! Сегодня у нас необычный урок по самой обычной теме . Тема урока: обобщение по теме «Показательная , степенная ,логарифмическая функции». А урок будет проходить в форме интеллектуального казино. Вопросы и задания будут касаться этой темы. Эпиграфом к нашему уроку пусть будут слова М.В.Ломоносова: «Математику только затем учить надо, что она ум в порядок приводит». За каждый правильный ответ получаете фишку (1 ум). Кто больше наберет умов , тот получает приз и отметку «5»; Давайте потренируемся: 1.С этим числом связанно много поверий ,пословиц .Во всех пословицах его используют как «много».Что это за число?
Итак, первый вопрос. 1.Имя этого ученого связано с понятием степени и радикала. Это французский учённый.  1)Карл Гаусс ; 2)Архимед ; 3) Эварист Галуа. 2. Найдите график логарифмической функции: А) б) в) 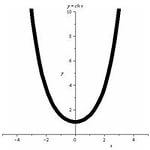 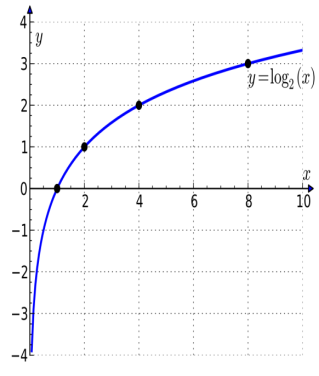 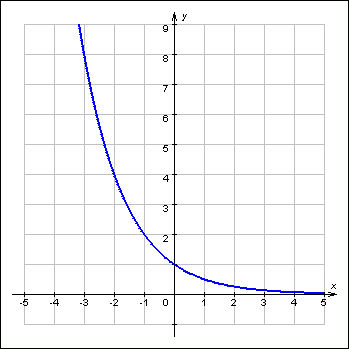 3. Найди значение выражения 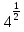 × ×  1) 16; 2)4; 3)8. 4. Найдите арифметический корень из числа Угадай слово: I. 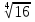 III. III. 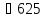 А) -4 б)2 в)4 а)5 б)25 в)-25 Р к г р з н II.  IV. IV. 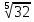 а) -1 б)1 в)17 а)4 б)2 в)-2 а о е у а ю Ответ: КОРА 5. Найдите площадь прямоугольника, если его длина и ширина выражены числами: 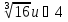 а)2 б)8 в)4 6. Что больше : сумма квадратов цифр или произведение квадратов 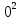 + +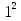 + +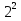 + … + + … + 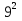 или или 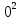 x x 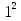 х х 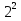 х…х х…х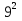 а) произведение б) сумма в) равны 7) найти значение выражения.  1)1; 2)2; 3)3 8) Что больше 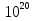 или или 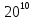 1) 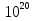 ; 2) ; 2)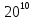 3) равны 3) равны9)Историческая справка: Числа Фибоначчи В начале XIII века в городе Пизе (Италия) жил большой знаток всевозможных соотношений между числами и весьма искусный вычислитель Леонардо ( с добавлением к его имени Пизанский). Его звали ещё Фибоначчи, что значит сын Боначчи. В 1202 году он издал книгу на латинском языке под названием «Книга об абаке» ( Incipit Liber, Abbaci composites a Leonardo filius Bonacci Pisano ), содержащую в себе всю совокупность знаний того времени по арифметике и алгебре. Это была одна из первых книг в Европе, учившая употреблять десятичную систему счисления. По обычаям того времени Фибоначчи участвовал в математических турнирах (публичное состязание в наилучшем и наиболее быстром решении трудных задач; нечто вроде наших математических олимпиад ) Леонардово искусство в решении числовых задач изумляло всех. Высокая репутация Фибоначчи привлекала однажды ( в 1225 г. ) в Пизу государя Римской империи Фридриха II, который приехал в сопровождении группы математиков, желавших публично испытать Леонардо. Одна из задач, предложенных на турнире, имела следующее содержание: Найти полный квадрат, остающийся полным квадратом как после увеличения его, так и после уменьшения на 5. Напомню, что полным квадратом называется число, из которого точно извлекается квадратный корень. Фибоначчи после некоторых размышлений нашел такое число. Оно оказалось дробным: 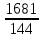 , или , или 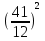 . . Действительно , 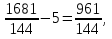 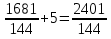 Иначе 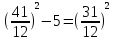 И 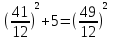 Какими соображениями руководствовался Фибоначчи во время турнира, этого мы никогда не узнаем, но задачу он решил блестяще. 10) логарифмическая комедия. Возьмём равенство 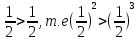 Прологорифмируем по осн. 2, т.к функция log 2X – возр., то знак не меняем. Log2 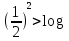 2 2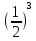 2 log2 ( 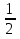 ) > 3 log2 ) > 3 log2 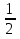 Разделим на log2 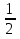 Получаем 2>3. где ошибка? 11) Итог урока. |