«Развитие мышления при решении задач по физике»
 Скачать 138.1 Kb.
|
МЕТОДИЧЕСКАЯ РАБОТАпо теме «Развитие мышления при решении задач по физике» Чебоксары – 2010 Содержание 1. Введение 3 2. О некоторых проблемах развития мышления при решении задач по физике и путях их решения 5 3. Заключение 12 4. Список использованной литературы 13 5. Приложения 14 Введение Решение физических задач в учебном процессе по физике занимает очень важное место. Это неудивительно, если учесть, что оно является одной из наиболее эффективных форм углубленного изучения и закрепления теоретического материала и развития мышления учащихся. Любая задача — это проблема, решить задачу — справиться с проблемой. Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия. Задача, которую ученик решает, может быть скромной, но если она бросает вызов любознательности ребенка и заставляет его быть изобретательным и ученик решает эту задачу собственными силами, то он сможет испытать ведущее к открытию напряжение ума и насладиться радостью победы. Такие эмоции, пережитые в восприимчивом школьном возрасте, могут пробудить вкус к умственной работе и на всю жизнь оставить отпечаток на уме и характере. Таким образом, учителю физики предоставляются великолепные возможности. Если он заполнит отведенное ему учебное время натаскиванием учащихся в шаблонных упражнениях, он убьет их интерес, затормозит их умственное развитие и упустит свои возможности. Но если он будет пробуждать любознательность учащихся, предлагая им задачи, соразмерные с их знаниями, и своими наводящими вопросами будет помогать им решать эти задачи, то он сможет им привить вкус к самостоятельному мышлению и развить необходимые для этого способности. Наибольший «эффект» в развитии мышления учащихся связан с применением не тренировочных задач, решаемых по одному образцу (когда меняются лишь числовые данные), а задач творческого характера. В книге «Творческие задачи по физике в средней школе» В.Г. Разумовский отмечает, что творческой задаче присуща существенная новизна в самом подходе к ее решению, а также необходимость поиска принципа решения. Однако чаще всего термин «существенная новизна» понимается каждым учителем по своему и по этому часто возникает спор: считать ли ту или иную задачу творческой. Конечно же, нельзя сделать четкой границы между задачей «творческой» и «логической». Если говорить строго, что всякая задача, не похожая на тренировочную (решаемую шаблонно), уже имеет элемент «проблемности», творческий характер, требует выхода за пределы прежней ситуации и поиска нового способа решения. Творческий компонент задачи в значительной мере усиливается: 1) если искомое неизвестное формулируется в терминах, не связанных непосредственно с используемой формулой; 2) если конкретные данные в задаче отсутствуют; 3) если в задаче не имеются все данные, необходимые для ее полного решения (которые ученик должен сам найти из таблиц и справочной литературы). О некоторых проблемах развития мышления при решении задач по физике и путях их решения Далее в своей работе я остановлюсь на проблемах, которые возникают при решении задач и развитии мышления учащихся в ходе решения задач. Первая проблема, с которой я столкнулся, и которую считаю типичной, заключается в том, что ученики не проявляют особого интереса к решению задач по физике, а часто — просто «боятся» физических задач. Как правило, это происходит в начале изучения курса физики, в 7 классе. Однако многие ученики продолжают испытывать негативное отношение к физическим задачам и в старшем звене. Известно изречение древних: лошадь можно подвести к воде, но нельзя заставить ее пить. Эта истина весьма применима к процессу обучения решению задач по физике. Никакая пылкая фантазия относительно формы проведения урока не сможет восполнить главного — устремленности школьника к овладению знаниями. И ее нужно будить. Чтобы пробудить интерес к решению задач, включению его мышления в процесс решения задачи я стараюсь выбрать задачу с интересным содержанием («внешний эффект»). Например, сравним 2 задачи: 1) Пирамида Хеопса при массе 5,84 Мт имеет фундамент площадью 5 га. Каково давление его на фундамент? Во сколько раз оно отличается от давления, развиваемое акулой при укусе, если последнее составляет 30  ?2) Какое давление на пол производит мальчик, масса которого 48 кг, а площадь подошв его обуви 320  ?Обе эти задачи по теме «Давление твердых тел» (7 класс) и решается с применением формулы для давления  . Однако первая задач более привлекательна для учеников, ибо ее условие содержит для них новые данные («эффект новизны») и связь с другими предметами (историей и биологией).Внешний привлекательный вид задачи лишь способствует активизации интереса ученика приступить к решению задачи. Но если задача окажется слишком сложной и непосильной для учеников, конечно же, его интерес к этой задаче быстро пропадет . Поэтому я стараюсь подбирать задачи для решения с учетом уровня развития знаний, умений и навыков данного класса и отдельно каждого ученика в данном классе. Однако, многие творческие задачи являются для большинства учеников особо трудными. Поэтому необходимо тщательно продумывать организацию их деятельности на уроке и руководство со стороны учителя этой деятельностью. Я использую для этого карточки с задачами различной степени сложности. Также успех решения задачи учеником зависит от того, как учитель умело направляет мышление учеников в «нужном направлении». Для этого я во время решения задач использую различные типы помощи ученикам. В случае затруднения учеников даю им в последовательном порядке устные подсказки или на карточках (в зависимости от ситуации) письменный текст. Ниже приведу пример задачи для решения, разбор решения и карточек для помощи (см. Приложение 1). В ходе решения задач и развития физического мышления любой учитель сталкивается с проблемой стандартного, шаблонного мышления учеников. Как правило, учащиеся, набрав определенный навык решения задач по данной теме, формуле или разделу, все остальные предлагаемые задачи пытаются решить шаблонно, не пытаясь особо вникать в физическую сущность явления, о котором говорится в условии задачи; применяют законы и формулы физики без учета их границ применимости. Естественно, шаблонные действия ученика, пытающегося найти ответ задачи, наносят непоправимый вред развитию логического и творческого мышления. Поэтому в целях «профилактики» шаблонного мышления и активизации творческого на уроках решения задач и в ходе обобщения и повторения, я вместе с остальными задачами даю задачи, шаблонное решение которых приводит к заведомо ложным результатам. После решения и детального разбора таких задач, как правило, многие ученики начинают учитывать «ошибку» этих задач. Приведу пример двух задач, которые я предлагаю в 9 классе при изучении темы «Перемещение при равноускоренном движении». Условия задач внешне ничем не отличаются, однако решения их и результаты различны. Задача 1. Автомобиль движется с ускорением  -4 м/с2. Найдите путь, пройденный им за 3 с, если его начальная скорость была равна 72 км/ч.Задача 2. Автомобиль движется с ускорением -4 м/с2. Найдите путь, пройденный им за 6 с, если его начальная скорость была равна 72 км/ч.Обе задачи решаются по формуле для пути, пройденного телом при равноускоренном движении 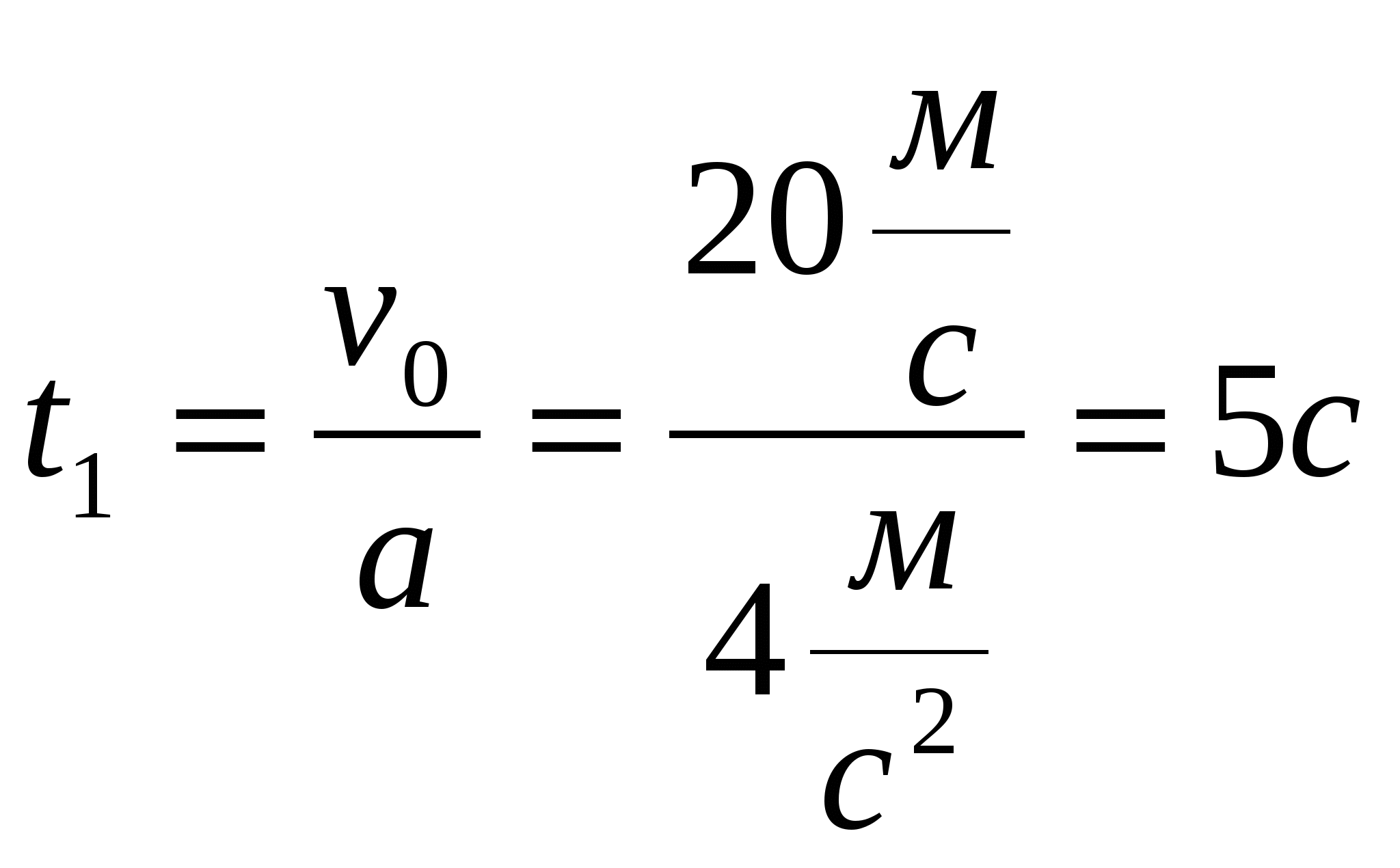 . Однако шаблонное решение задачи по этой формуле во второй задаче приводит к абсолютно неверному результату, т.к. автомобиль, о котором говорится в обоих задачах двигается равнозамедленно и останавливается через  . Поэтому во второй задаче автомобиль через 5 с остановится и в последнюю 6-ю секунду не будет двигаться. Следовательно, ученики, исследовав последнее обстоятельство, в формулу для пути должны подставить время не 6 с, а 5 с.Шаблонность представляет собой автоматизм в действиях, «привычку» действовать по соответствующему алгоритму. В то же время решение задач некоторых разделов физики (например, на применение II закона Ньютона) предусматривает использование алгоритмического подхода. При решении таких задач искусство учителя заключается в том, что он своевременно должен заметить момент перехода алгоритмического способа решения в шаблонный. Многие учителя и ученики считают, что чем больше задач они успевают решать за один урок или за несколько уроков по данной теме, тем больше развивается логическое мышление и приобретается больше навыков решения задач. Бесспорно: чем больше решенных задач — тем больше становится опыт ученика, обогащаются умения и навыки. Однако из своего опыта работы я могу утверждать, что количество решенных задач не является залогом развития творческого мышления. Особенно сложно привлечь всех учащихся класса к процессу решения задач при фронтальном способе работы, когда многие настроены не на обсуждение решения задачи, а на поглощение «готового продукта» коллективной деятельности. Важно, чтобы каждый ученик принял непосредственное участие в процессе решения задач. Чем больше самостоятельных элементарных операций произведет каждый учащийся при этом, тем больше мыслительных операций совершит он. В курсе физики очень много задач. Среди них встречается достаточное количество типичных по своему содержанию и решению задач. Однако идея решить все типы задач кажется абсурдной. Мне кажется, учитель не должен ставить задачу — решить все задачи школьного курса физики. Его старания должны быть направлены на обучение учащихся методам решения задач, анализа их условий, проверки и оценки полученных результатов. Научить методам решения задач означает, что учитель должен обучать учащихся: 1) понимать условие задачи; анализировать явления, происходящие в задаче; 2) самостоятельно находить пути решения данной задачи, установив связь между рассматриваемыми явлениями и физическими величинами; 3) реализовать найденную идею решения и получить окончательный ответ; 4) проверять решение, оценить критически полученный результат и указывать на другие возможные способы решения (см. Приложение 2). На первом этапе, в ходе ознакомления с условием задачи, успех зависит от того, насколько ученик самостоятельно может ставить перед собой и дать ответы на следующие вопросы: «О каком физическом явлении идет речь? Что дано Что нужно найти. Определяется ли неизвестная физическая величина данными задачи. Или они недостаточны, или же чрезмерны? Почему задача сформулирована именно так, а не иначе? На втором этапе ученик должен, рассмотрев взаимосвязи между данными величинами и искомой величиной, наметить идею решения задачи с указанием законов, необходимых для этого. Должен также обосновать свой выбор: почему он хочет решить задачу именно выбранным путем. В ходе реализации решения задачи, важно, чтобы ученик был уверен в правильности каждого своего шага и использовал бы только те формулы и закономерности, в достоверности которых не сомневается. Применение в ходе решения задачи формул и рассуждений «сомнительного характера» приводит к получению сомнительных же результатов. После получение ответа, необходимо научить ученика критически подходить к полученному решению, искать пути проверки полученного результата. Многие не уделяют должного внимания на последний этап, считая его малозначительным. Но разве можно говорить о творческом и логическом мышлении ученика, если последний, решая задачу на нахождение массы молекулы, получил ответ равный нескольким тоннам и нисколько не подверг сомнению этот результат?.. Конечно же в школьном курсе физики недостаточно времени на детальный разбор каждой задачи. Однако при правильном планировании учебного процесса учитель может достаточное время уделить на развитие мышления учащихся в процессе решения задач. Во время уроков решения задач, обобщения и повторения пройденного материала, я стараюсь вслух задавать все вопросы, названные в таблице приложения 2 и отвечать на них. Этого же требую от учеников. Такой подробный разбор решения задачи, акцентированный именно на показ хода логических рассуждений при решении, создает благоприятные предпосылки для возникновения мышления учащихся в ходе решения задач. Часто меня интересует вопрос не столько связанный с получением правильного ответа задачи, а то - какие умозаключения делал ученик при решении. Есть ли в его рассуждениях хоть частичка «творчества». Такой анализ несет в себе очень богатую информацию для моей дальнейшей работы в направлении развития мышления учащихся. Завершающим этапом любого процесса обучения является контроль. Контрольные задачи я всегда составляю таким образом, чтобы на «5» их могли решить лишь ученики, у которых наиболее (и в достаточной степени) развито логическое мышление, общефизические навыки и умения. Этого добиваюсь тем, что любой комплект задач (их как правило 3 или 4 в одном варианте) содержит задачи с разной степенью сложности, охватывающих весь учебный материал по данной теме. Таким образом, я даю ученикам, усвоившим обязательный минимальный уровень знаний, получить удовлетворительную оценку и практически исключаю возможность получения «случайных» оценок (особенно «5» и «4»). В качестве примера привожу текст контрольной работы, проведенной в I четверти 2003-2004 учебного года в 8-х классах по теме «Количество теплоты. Изменение внутренней энергии тела при теплопередаче (см. приложение 3). Анализ решений и результатов контрольной работы в 8 «А», «Б», «В», «Г», «Д», «Е» классах показывает следующее: 1) Количество учеников, получивших «4» и «5» в 8 «А» и 8 «Б» классах составляет 70-80% (в этих классах уровень сформированности мышления выше), причем более 50% учащихся решали (некоторые с ошибками) третью задачу, которая требовала умения выстраивать достаточно непростую цепочку умозаключений. 2) В остальных классах количество учеников, выполнивших работу на «4» и «5» не превышает 30-50%. Причем, многие учащиеся этих классов решили первую задачу, не требующую «особого напряжения ума» и рассчитанную на применение обязательных по программе минимальных знаний. Большинство учащихся не приступило даже к выполнению третьего задания, которое оказалось им не под силу. 3) Именно в 8 «А» и 8 «Б» классах оказалось больше работ, сопровождаемых решение задач с обсуждением хода решения. Заключение В этой работе я сделал попытку лишь выделить наиболее значимые проблемы, возникающие при развитии мышления в ходе решения задач по физике и дать некоторые пути их решения. Конечно же, данная проблема гораздо шире и требует к себе всестороннего изучения. Однако можно уверенно утверждать, что на уроках физики необходимо развивать мышление учащихся, т.к. это связано с развитием творческой всесторонне развитой личности. Наилучшие условия для развития мышления мы имеем при решении физических задач, т.к. существует очень большое количество и разнообразие задач по физике, что дает возможность применения различных способов и методов их решения. Развитие мышления учащихся при решении задач — процесс очень кропотливый и продолжительный во времени. Очень многое в этом деле зависит от мастерства педагога, от его умения грамотно планировать материал уроков, от способности умело направлять усилия учеников в нужном направлении. Список использованной литературы
Приложение 1 Задача: В стакан наливают жидкость. Выясните, при каком условии центр тяжести стакана с жидкостью будет занимать наинизшее положение. Р   ешение: Это качественная задача. Ее решение требует нетривиального способа рассуждения. Оно может быть следующим: пусть центр масс пустого стакана находится в точке С (рис. 1). Тогда при наливании воды в стакан центр масс системы стакан-вода будет понижаться, т.к. при этом увеличивается масса ниже центра масс стакана. Очевидно, так будет продолжаться до тех пор, пока центр масс не сравняется с уровнем воды в стакане. При последующем же добавлении жидкости центр масс не сравняется с уровнем воды в стакане. При последующем же добавлении жидкости центр масс начнет повышаться. Таким образом, наинизшее положение центра масс будет при условии, когда он находится на уровне жидкости.Карточки с подсказками к данной задаче. Карточка 1. Отметьте на рисунке точкой приблизительное положение центра масс пустого стакана. Подумайте , как будет изменяться относительно этой точки положение общего центра масс стакана и жидкости по мере наливания последней в стакан. Это поможет вам решить задачу. Карточка 2. Отметьте на рисунке точкой приблизительное положение центра масс пустого стакан. При наливании в стакан жидкости общий центр масс стакана и жидкости вначале будет понижаться, т.к. увеличивается масса содержимого ниже центра масс стакана. Подумайте, до каких пор это будет происходить, и ответьте на вопрос задачи. Карточка 3. Точкой С на рисунке 1 отмечен центр масс пустого стакан. При наливании жидкости в стакан общий центр масс стакана и жидкости С начнет понижаться, т.к. увеличивается масса содержимого ниже центра масс стакана (рис. 1). В какой-то момент положения центров масс стакана и жидкости совпадут с уровнем жидкости в стакане. Подумайте, как будет изменяться положение центра масс при дальнейшем наливании жидкости, а затем ответьте на вопрос, содержащийся в задаче. Приложение 2 Таблица «Как искать решение задачи»
Приложение 3 Текст контрольной работы по теме «Количество теплоты. Изменение внутренней энергии тела при теплопередаче» I вариант 1. Какое количество теплоты необходимо для нагревания алюминиевой детали массой 50 г от температуры 40С до температуры 90С? 2. На сколько градусов можно нагреть серебро массой 40 г, добавив ему 680 Дж энергии? 3. Чугунный утюг массой 2 кг нагрели на газовой горелке от 20 до 220С. Определите массу газа, израсходованного на нагревание утюга, считая, что потери теплоты не было (Удельная теплоемкость чугуна 540 Дж/кгС, удельная теплота сгорания газа 4,4Дж/кг). II вариант 1. При сжигании бензина выделилось 2,3109 Дж энергии. Определите массу сгораемого бензина (Удельная теплота сгорания бензина 4,6107 Дж/кг). 2. На сколько градусов охладится лед массой 40 кг, если у него отнять 400 кДж теплоты? (Удельная теплоемкость льда 2100 Дж/кгС) 3. Сколько горячей воды, температура которой 90С, надо добавить к холодной воде массой 5 кг при температуре 10С, чтобы температура смеси оказалась равной 40С? | ||||||||||||