Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

«Производная и её применение к исследованию функций»



Скачать 115.77 Kb.
Название«Производная и её применение к исследованию функций»
Дата18.04.2016
Размер115.77 Kb.
ТипДокументы

Тема: «Производная и её применение к исследованию функций».

Группа 234
Курс II
Тип урока: Повторительно - обобщающий.
Методы обучения:

  1. Опрос, беседа

  2. Наглядные: демонстрация материалов с помощью мультимедиа комплекса

  3. Тестирование (с помощью системы интерактивного опроса «Вердикт»)

  4. Практические задания (исследование).


Цели:

Дидактические (общеобразовательные):

  1. Обобщение и систематизация, применение знаний о производной к иcследованию свойств функции на основе анализа, построение графиков.

  2. Установление межпредметных связей (с физикой).

  3. Использование мультимедийного комплекса для повышения интенсивности аналитической деятельности обучающихся, стопроцентного охвата контролем уровня в применении производной к исследованию свойств функций.


Развивающие:

  1. Способствовать формированию ключевых компетенций: на основе обобщения и анализа проводить исследование по заданным параметрам, определять алгоритм действий, обобщать данные.

  2. Использовать источники информации (конспекты, учебники, справочники, таблицы) отбирать нужную информацию.


Воспитательные:

  1. Формировать коммуникативную культуру ( сотрудничество, умение работать в группе, общаться на протяжении всей общегрупповой деятельности ).



Оборудование:

    • Компьютер

    • Экран

    • Мультимедийный комплекс

    • Система интерактивного опроса «Вердикт»

    • Карточки.


Формы организации учебной деятельности:

  • Фронтальная

  • Индивидуальная

  • Работа в малых группах.


Мотивация:

Актуальность темы урока состоит в подготовке обучающихся в предстоящим итоговым аттестационным испытаниям.
Ожидаемые результаты:

  1. Формирование, закрепление и систематизация компетенций обучающихся при выполнении различных по степени сложности заданий.

  2. Повышение интереса к предмету.

  3. Формирование навыков сотрудничества, взаимопонимания.


ХОД УРОКА.

  1. организационный момент.

  • Приветствие

  • Проверка явки обучающихся (рапорт старосты).

  • Создание эмоционального настроя у обучающихся на работу.

  • Подчеркнуть значимость темы в математике.


На экране – слайд 1 презентации с портретами авторов теории дифференцирования функций ( И. Ньютона и Г. Лейбниц.)
Тема: « Производная и её применение к исследованию функций»
А. Франс (1844-1924 г.) : «Чтобы переварить знания, надо поглощать их с аппетитом».
Вопрос преподавателя к учащимся: «Когда приходит аппетит»? (Обучающиеся: «Аппетит приходит во время…работы».)
(Учитель озвучивает, учащиеся записывают тему в тетрадях)

Учитель: Сегодня у нас урок обобщения по данной теме и проверки уровня её усвоения.
II. Устные упражнения.

  1. Что называется производной?


Слайд 2.


  1. Если на дороге произошла авария, то инспектора ГИБДД интересует скорость в момент аварии. Как она называется?

(Ответ: мгновенная скорость)

Слайд 3.


  1. Как связана мгновенная скорость и производной?

Слайд 4.

Изображения движения.

(Ответ: Производная - это скорость изменения функций)
Учитель: Открытие Ньютона – Лейбница явилось поворотным пунктом в истории естествознания. Оказалось, что количественные характеристики различных процессов в физике, химии, биологии, технике могут быть выражены на языке математического анализа, изучающего связи между функциями и их производными.

Приведите примеры из функций

(Скорость, ускорение, мощность, работа, сила….)


  1. В чем заключается геометрический смысл производной?

(значение производной в функции в точке равно угловому коэффициенты касательной к графику функции в этой точке).

Слайд 5.



  1. На предложенных рисунках изображены графики функций и касательные к ним в точке а. Укажите функцию, производная которой в точке а равна 1?

Слайд 6

Даны четыре чертежа. Обучающимся предлагаются вопросы к ним.

- Укажите функцию, производная которой равна 1.

- чему равен тангенс угла наклона касательной к графику функции в точке с абсциссой х=а? (производная в точке с абсциссой х=а)

- чему равен угол наклона касательной к оси абсцисс?
Блиц - опрос с помощью системы интерактивного опроса «Вердикт»

(5 чертежей )
1. Чему равна производная функции в данной точке? ( Рис.1 и 2)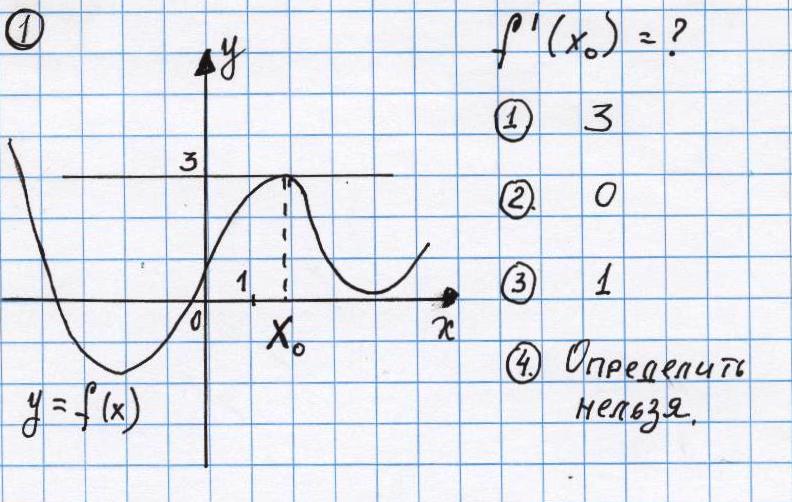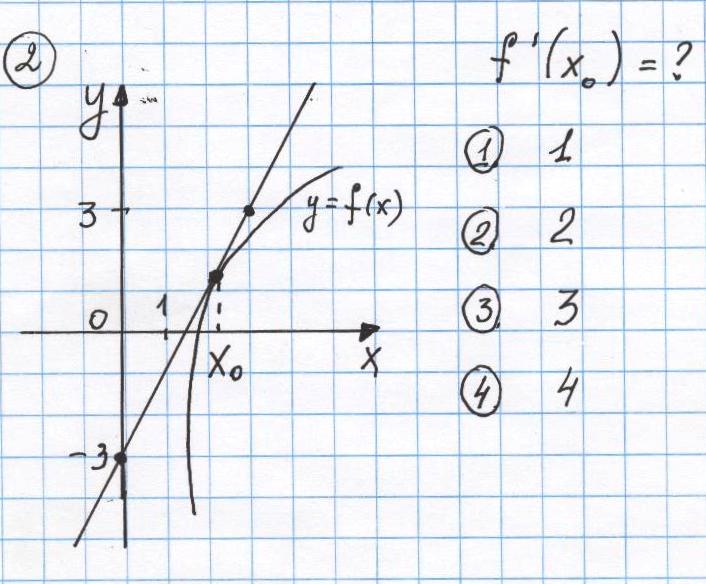


2.Чему равен тангенс угла  ? (рис.3 и 4)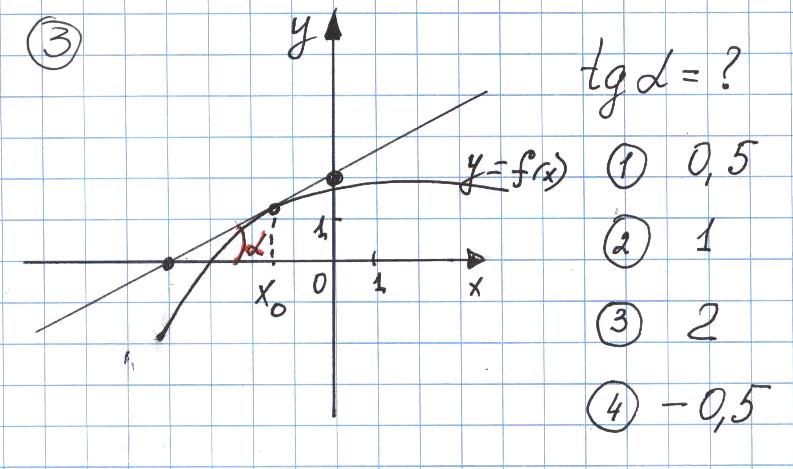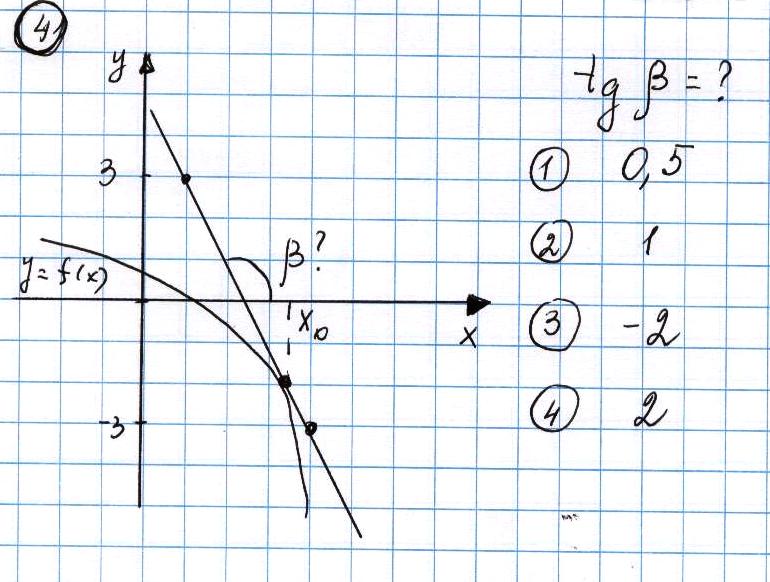


3.Чему равен угол наклона касательной к оси абсцисс? (рис 5)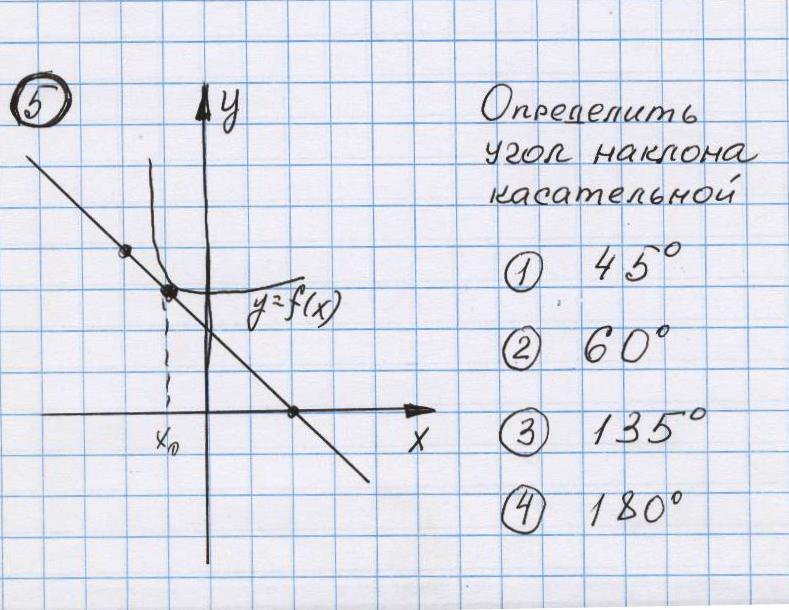



(Проверка и оценка проводится сразу. Результаты - на экране)
Продолжение работы по исследованию свойств функций.

  1. Назовите по данным чертежа промежутки монотонности и экстремумы функции.

Слайд 7
(обучающиеся отвечают.

Дополнительные вопросы : - где перегиб? - где разрыв?)


7. Используя график функции, найдите интервалы монотонности и точки экстремума, а также наибольшее и наименьшее значения функции (Устно).

Слайд 8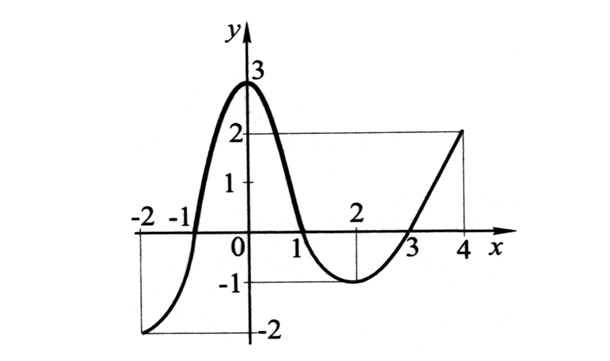



III. Конкурс “Верно-Неверно».

Выдаются листы с вопросами. Каждая «команда» должна ответить «да» или «нет». Затем – взаимооценка вслед за комментарием. Сравнения с правильным вариантом ответов.
Вопросы:

1. Верно ли, что в точке возрастания функции её производная больше 0?

2. Верно ли, что если прозводная функции равна нулю в некоторой точке, то в этой точке имеется экстремум ?

3. Верно ли, что производная произведения равна произведению производных?

4. Верно ли, что наибольшее и наименьшее значение функции на некотором отрезке наблюдаются или в стационарных точках или на концах отрезка?

5.Верно ли, что любая точка экстремума является критической точкой?

(взаимопроверка – обмен работами между группами )

(Оценка по пятибалльной системе)

После листы сдаются учителю.
Преподаватель приводит высказывание Д. Юнга: «Когда математические задачи решаются легко, это служит наилучшим доказательством того, что силы, которые математика должна развить, уже развились».

Вот и проверим.
IV. Решение упражнений (в тетрадях). Обучающиеся выполняют задание в малых группах. Каждой группе – одно из приведённых ниже упражнений

Предполагается ответ обучающихся с демонстрацией через проектор хода решения. (Возможно и использование интерактивной доски).

(Возможен также вариант проверки в тетрадях в зависимости от скорости выполнения задания).

  1. Найти наибольшее и наименьшее значение функции

y=Х4-8Х2-5 на [-1;2].
Ответ: Max f (х) = f (0) = -5; Min f (X) = f (2) = -2 на [-1;2].



  1. Найти интервалы монотонности функции у=2х3-3х2-36х+40


Ответ: функция возрастает на промежутках(- ;-2] и [3;+ ) и убывает на промежутке [-2;3]


  1. Найти точи экстремума функции

у=3х4-4х3+2

Ответ: х=-1 – точка максимума; х= 1 – точка минимума.
V. Проверка усвоения материала.
Учитель совместно с обучающимися повторяет план построения графика.

Затем – слайд 9 с планом.

Каждой группе – построить график функции (задания по учебнику).

  1. № 928 (1)

  2. № 927 (2)

  3. № 930 (2)

  4. № 931 (2)


Обучающиеся выполняют работу в тетрадях, помогая друг-другу.

Разрешается консультация учителя.

Работы проверяются учителем с оценкой в журнал.
VI. Релаксация.

Подведение итогов. ( Преподаватель оценивает общую работу, озвучивает оценки за индивидуальные ответы.

Распечатка интерактивного опроса выдаётся обучающимся.

Оценка в журнал – после суммирования оценок II – III части.

Ещё одна оценка – после проверки тетрадей.)

Преподаватель : «Следует ли проводить подобные уроки?» (Другие вопросы. Обсуждение урока).

Учащимся предлагается оценить самых активных дополнительным баллом.


Слайд 10

Домашнее задание

Параграфы 48 – 52

«Проверь себя» на странице 248

№№ 1, 2, 3 (1), 4.
Литература:

  1. Алимов Ш. А. и др. « Алгебра и начало анализа. 10-11» Просвещение 2011 год.

  2. Смирнова Л. . «Устные упражнения на уроках математики» - М. Просвещение 1996 год.

  3. Статья Фестиваля педагогических идей. « Открытый урок» (Интернет)


ФЗИС.

«Верно — не верно»

(Вписать «Да» или «Нет»).


  1. Верно ли, что в точке возрастания функции ее производная больше нуля?

Ответ:




  1. Верно ли, что если производная функции в некоторой точке равна нулю, то в этой точке имеется экстремум?


Ответ:




  1. Верно ли, что производная произведения равна произведению производных?

Ответ:




  1. Верно ли, что наибольшее и наименьшее значения функции на данном отрезке находятся либо в стационарных точках, либо на концах отрезка?

Ответ:




  1. Верно ли, что любая точка экстремума, является критической?


Ответ:

Карточка № 1
Найти наибольшие и наименьшее значение функции.
у = х4 — 8х2 — 5 на [-1;2]


Карточка №2

Найти интервалы монотонности функции.
у = 2х3 — 3х2 — 36х + 40


Карточка №3

Найти точки экстремума функции.
у = 3х4 — 4х3 + 2


Самостоятельная работа по теме:

«Исследование функций с помощью производной»

Цель работы: научиться применять производную при исследовании функций.

Теоретический материал

Общая схема исследования функций с помощью производной

  1. Нахождение области определения функции.

  2. Нахождение корней функции

  3. Определение промежутков знакопостоянства функции.

  4. Монотонность функции.

Нахождение производной функции по таблицам и правилам.

Нахождение критических точек.

( точек, в которых производная равна нулю или не существует).

Определение промежутков возрастания и убывания функции

(промежутков, на которых производная положительна или отрицательна).

5.Определение экстремумов функции.

6.Дополнительные точки. Уточнение графика функции по точкам (произвести окончательное уточнение графика, в особенности на участках, где информация о нем недостаточна).

Данную схему можно варьировать в зависимости от конкретных особенностей функции, переставлять отдельные этапы, некоторые из них опускать, какие-то, наоборот, добавлять.
Индивидуальные задания для обучающихся по пособию Богомолова Н.В. «Практические занятия по математике»

(М.: Высшая школа, 2008)

  1. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 3x – x3

  1. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x3 – 12x

  1. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 16x3 – 12x

  1. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 5x - 53x3

5. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 14x3 – 3x – 1
6. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 2 + 32x- 12x3

7. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 1 + 4x - 13x3
8. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 13x3 – x + 3

9. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 4x3 – 6x2
10. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 3x2 – x3

11. Исследуйте функцию с помощью производной и постройте ее график:

f(x) =3x2 – 2x3
12. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x3 + 3x2

13. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 4x3 - 6x2
14. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = -x3 -3x2

15. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 2x3 + 3x2 - 2
16. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 1 + 3x2 – 2x3

17. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 1 – 3x2 – x3
18. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x3 - 3x2 + 3

19. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 23x3 – 2x2 + 1
20. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 2 + x2 - 13x3

21. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 4 + 3x – x2 - 13x3
22. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 13x3 + 12x2 -2x - 13

23. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x3 – 6x2 + 9x - 3
24. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x3 + 6x2 + 9x + 8

25. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = 8x2 - x4 - 7
26. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x4 - -2x2 – 5

27. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x4 -2x2 – 6
28. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = -x4 + 2x2 + 3

29. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x3 – 3x
30. Исследуйте функцию с помощью производной и постройте ее график:

f(x) = x3 + 3x2