Показательная и логарифмическая функции (2 ч)
 Скачать 60.67 Kb. Скачать 60.67 Kb.
|
| Тема урока: Показательная и логарифмическая функции (2 ч) Цели: выработка умений самостоятельно применять знания и осуществлять перенос их в новые условия.повторить свойства логарифма и логарифмической функции; повторить свойства показательных функций, способы решения показательных уравнений и неравенств, закрепить навыки и умения применения знаний по теме к решению упражнений. Тип урока: урок систематизации знаний. Ход урока I. Устная работа
II. Система упражнений.
в) h(x)=Lg(x-4); г)q(x)=(1/5)х; д)u(x)=0,9x.
б) Log1,79 и Log1,75; в) Log0,44 и Log0,416; г)Log0,91/16 и Log0,97/8; д) log0,9x и Log0,9(5x).
III. Повторение свойств:
IV. Разминка. Решение кроссворда Каждый получает кроссворд, в котором нужно в результате решения получить ключевое слово. (Логарифм). 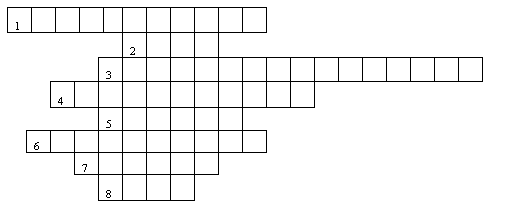
Ответы:
Вариант 1. 1. Решите неравенство 5х >25. План и примерное оформление решения:
2. Решите неравенство 6х<36. Вариант 2. 1. Решите неравенство (2/3)х >8/27. План и примерное оформление решения: 1) Представьте число 8/27 как значение показательной функции у=(2/3)х, т.е. как степень с основанием 2/3: 8/27 = (2/3)3; (2/3)х >(2/3)3. 2) Определите характер монотонности функции (возрастающая функция или убывающая) у= (2/3)х, сравнив основание 2/3 с единицей: у=(2/3)х убывающая, так как 2/3<1. 3) Используя данные о характере монотонности и заданную зависимость между значениями функции ((2/3)x>(2/3)3), определите соотношение между аргументами: у= (2/3)х убывающая, и (2/3)х>(2/3)3, следовательно, х<3. 4) Запишите решение полученного проcтейшего неравенства х<3: (-∞; 3). Ответ: (-∞;3). 2. Решите неравенство (1/2)х<1/16. Вариант 3. 1. Решите неравенство (3/4)х ≤4/3. План и примерное оформление решения: 1) Представьте число 4/3 как значение показательной функции у=(3/4)х: 4/3= (3/4)-1, (3/4)х≤(3/4)-1. 2) Определите характер монотонности функции (возрастающая функция или убывающая) у=(3/4)х: у= (3/4)х - убывающая, так как 3/4<1. 3) Используя данные о характере монотонности и заданную зависимость между аргументами: у=(3/4)х -убывающая, и (3/4)х≤(3/4)-1; следовательно, х≥-1. 4) Запишите решение полученного проcтейшего неравенства: (-1;∞). Ответ: (-1;∞). 2. Решите неравенство (7/2)х ≥2/7. Вариант 4. 1. Решите неравенство 12х≥ 1/12 План решения: 1) Представьте число 1/12 как значение показательной функции у=12х. 2) Определите характер монотонности функции (возрастающая функция или убывающая) у=12х 3) Используя данные о характере монотонности и заданную зависимость между аргументами. 4) Запишите решение полученного проcтейшего неравенства. 2. Решите неравенство 2,5х ≥2/5. VI. Самостоятельная работа 2 (СО) Вариант 1 1. Решите неравенство Log4x<3. План и примерное оформление решения: 1) Представьте правую часть неравенства (число 3) в виде значения логарифмической функции у=Log4x, т.е. как логарифм с основанием 4: 3= Log443, тогда Log4x 2)Рассмотрите логарифмическую функцию у=Log4x и определите характер монотонности (возрастающая функция или убывающая), сравнив основание 4 с единицей: у=Log4x — возрастающая, так как 4>1. 3) Определите соотношение между аргументами (х и 43), используя данные о характере монотонности и заданную зависимость между значениями функции.Указание: D(Log)=(0;∞).  у=Log4x- возрастающая, и Log4x< Log443; следовательно, х<43 у=Log4x- возрастающая, и Log4x< Log443; следовательно, х<43x>0 4) Запишите решение полученной системы: (0; 43). Ответ: (0;64). 2. Решите неравенство Log3x>2. Вариант 2 1. Решите неравенство Log1/2x<4. План и примерное оформление решения: 1) Представьте правую часть неравенства (число 4) в виде значения логарифмической функции у=Log1/2x, т.е. как логарифм с основанием 1/2: 4= Log1/2(1/2)4, тогда Log1/2x 2)Рассмотрите логарифмическую функцию у=Log1/2x и определите характер монотонности (возрастающая функция или убывающая), сравнив основание 1/2 с единицей: у=Log1/2x — убывающая, так как 1/2<1. 3) Определите соотношение между аргументами (х и (1/2)4), используя данные о характере монотонности и заданную зависимость между значениями функции.Указание: D(Log)=(0;∞).  у=Log1/2x- убывающая, и Log1/2x< Log1/2(1/2)4; следовательно, х>(1/2)4 у=Log1/2x- убывающая, и Log1/2x< Log1/2(1/2)4; следовательно, х>(1/2)4x>0 4) Запишите решение полученной системы: (1/16; ∞). Ответ: (1/16; ∞) . 2. Решите неравенство Log1/2x>2. Вариант 3. Решите неравенства: а) Log5x<1; б)Log5x>4. План решения: 1) Представьте правую часть неравенства в виде значения логарифмической функции у=Log5x, т.е. как логарифм с основанием 5. 2)Рассмотрите логарифмическую функцию у=Log5x и определите характер монотонности (возрастающая функция или убывающая), сравнив основание 5 с единицей. 3) Определите соотношение между аргументами, используя данные о характере монотонности и заданную зависимость между значениями функции. 4) Запишите ответ данного неравенства. Вариант 4. Решите неравенства: а) Log1/8x>1; б)Log1/8x<1/3. План решения: 1) Представьте правую часть неравенства в виде значения логарифмической функции у=Log1/8x, т.е. как логарифм с основанием 1/8. 2)Рассмотрите логарифмическую функцию у=Log1/8x и определите характер монотонности (возрастающая функция или убывающая), сравнив основание 1/8 с единицей. 3) Определите соотношение между аргументами, используя данные о характере монотонности и заданную зависимость между значениями функции. 4)Запишите ответ данного неравенства. VII. Итог урока. |