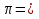Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

«Усиление практической направленности математики через организацию систематического проведения практических и лабораторных работ»



Скачать 442.46 Kb.
Название«Усиление практической направленности математики через организацию систематического проведения практических и лабораторных работ»
страница3/3
Дата18.04.2016
Размер442.46 Kb.
ТипДокументы
1   2   3

Вычисление периметра и площади квадрата.

  1. Измеряю сторону квадрата: а=

  2. Нахожу площадь по формуле:S=

  3. Если нужно, перевожу единицы площади в квадратные сантиметры.

  4. Записываю ответ.

  5. Вычисляю периметр квадрата по формуле: Р=

  6. Записываю ответ.


Вывод:

Практическая работа по теме:

«Вычисление длины окружности и площади круга»

и обобщать результаты своей работы.

  • Оборудование: 3 модели круга разного радиуса ,циркуль ,масштабная линейка, нитка, ножницы, клей-карандаш.

  • Гипотеза: (1.О соотношении длины окружности и её радиуса;

2.О том, как меняется длина окружности в зависимости от радиуса ( если радиус увеличился (уменьшился) в k раз, то длина окружности……………… )

Ход работы

Вычисление длины окружности.

1-ая часть.

  1. Провожу и измеряю радиус окружности ( в мм): R1 =

  2. Вычисляю по формуле C1 = длину 1-ой окружности , округлив значение числа «пи» до десятых: =

  3. Записываю решение:

  4. Записываю ответ:

2-ая часть.

  1. Провожу и измеряю радиус 2-ой окружности ( в мм) : R2 =

  2. Вычисляю по формуле C2 = длину 2-ой окружности , округлив значение числа «пи»до десятых: =

  3. Записываю решение:

  4. Записываю ответ:

Сравнив результаты 1-ой и 2-ой части, делаю

вывод: ( о том, как меняется длина окружности в зависимости от радиуса ( если радиус увеличился (уменьшился) в ….. раз, то длина окружности……………… )

3-ая часть

  1. Измеряю длину 1-ой и 2-ой окружности

с помощью нити, предварительно проведя клеем-карандашом по окружности и, пока клей не высох, проложить нитку точно по контуру окружности и аккуратно отрезать ее на стыке.

Снять нитку с картона и очень точно измерить ее длину в миллиметрах. Эту величину назовем длиной окружности (С).

  1. Записываю значение :.с1 =………… ; с2 =……….

3.Сравниваю результаты с результатами 1-ой и 2-ой части
Делаю вывод: (выявляя закономерность:

длина окружности больше её радиуса примерно в … раз

Вычисление площади круга

  1. Провожу и измеряю радиус 3-ей модели круга: R3 =

  2. Вычисляю по формуле S= площадь круга, округлив значение до единиц: =

  3. Записываю решение:

  4. Записываю ответ :.

Делаю вывод ( о том как найти длину окружности и площадь круга, зная радиус):

Практическая работа в 5 классе.

«Нахождение периметра и площади треугольника».

Цель работы: овладение навыками измерения сторон треугольника и построения высоты треугольника.

Оборудование:масштабная линейка, треугольник, модель треугольника.

Ход работы

1-ая часть: Вычисление периметра и площади треугольника, построенного в тетради.

  • Построить треугольник АВС.

  • Сделать необходимые измерения.

  • Записать результаты измерений.

  • Вычислить периметр построенного треугольника по формуле Р=…..

  • Записать решение.

  • Записать ответ.

  • Провести высоту BD.

  • Достроить рисунок до прямоугольника АКМС.

  • Вычислить площадь построенного прямоугольника, сделав необходимые измерения.( Записать результаты измерений……..)

  • Записать решение.

  • Найти площадь треугольника АВС .

  • Записать решение

  • Записать ответ.

  • Составить и записать формулу для нахождения площади треугольника АВС S=……….

2-ая часть: : Вычисление периметра и площади модели треугольника.


  • Сделать необходимые измерения.

  • Вычислить периметр треугольника.( Р=….. )

  • Записать ответ.

  • Провести высоту.

  • Вычислить площадь треугольника. (S=……….)

  • Записать ответ

Сделать вывод по проделанной работе.

Лабораторная работа

«Нахождение площади поверхности и объёма куба и прямоугольного параллелепипеда».
Цель: научиться вычислять по формулам площади поверхности и объёма куба и прямоугольного параллелепипеда, выполнив необходимые измерения, и обобщать результаты выполненной работы.

Оборудование: модели кубов и прямоугольных параллелепипедов, масштабная линейка, микрокалькулятор.

Ход работы.

Нахождение площади поверхности и объёма куба.

  1. Измеряю длину ребра куба: а=

  2. Вычисляю площадь его поверхности по формуле: S=

  3. Вычисляю объём куба по формуле: V=

  4. Записываю ответ.

• *

Нахождение площади поверхности и объёма прямоугольного параллелепипеда

  • Измеряю длину: а=

ширину: в=

высоту: с=

прямоугольного параллелепипеда.

  • Вычисляю площадь его поверхности по формуле: S=

  • Вычисляю объём прямоугольного параллелепипеда по формуле: V=

  • Записываю ответ.

Вывод:

Практическая работа в 7 классе

«Построение медиан, биссектрис и высот треугольника путём перегибания модели треугольника».

Цель: овладение навыками построения медианы, биссектрисы и высоты треугольника путём перегибания модели треугольника.

Оборудование: модель остроугольного треугольника МТК,модель прямоугольного треугольника RPS, модель тупоугольного треугольника АВС , ручка или карандаш.

Опорные знания: знание определений медианы, биссектрисы и высоты треугольника.

Гипотеза( о том, как будут пересекаться медианы, биссектрисы и высоты в треугольнике.)

Ход работы

1-ая часть.

  1. На модели треугольника RPS совместить точки R и S, не перегибая модель.

  2. На стороне RS отметить точку Y – середину этой стороны.

  3. Перегнуть модель треугольника по отрезку PY.

  4. На модели треугольника RPS совместить точки R и P, не перегибая модель.

  5. На стороне RР отметить точку X – середину этой стороны.

  6. Перегнуть модель треугольника по отрезку SX.

  7. На модели треугольника RPS совместить точки S и P, не перегибая модель.

  8. На стороне SР отметить точку Z – середину этой стороны.

  9. Перегнуть модель треугольника по отрезку RZ.


Сделайте вывод( о том, как называются отрезки PY, RZ, SX и о том, как они пересекаются в треугольнике.)
2-ая часть.

  1. На модели треугольника АВС совместите луч АВ с лучом АС ( чтобы они стали совпадающими) и перегните модель.

  2. На линии сгиба отметьте точку, лежащую на стороне ВС и обозначьте её -т. Е.

  3. На модели треугольника АВС совместите луч ВА с лучом ВС ( чтобы они стали совпадающими) и перегните модель.

  4. На линии сгиба отметьте точку, лежащую на стороне АС и обозначьте её -т. F.

5. На модели треугольника АВС совместите луч СВ с лучом СА ( чтобы они стали совпадающими) и перегните модель.

6.На линии сгиба отметьте точку, лежащую на стороне АВ и обозначьте её -т. D.
Сделайте вывод( о том, как называются отрезки BF, AE, CD и о том, как они пересекаются в треугольнике.)
3-ья часть.

  1. Модель треугольника МТК перегните так, чтобы: а) линия сгиба начиналась в т. Т и б) луч К и луч М стали направленными в одну сторону и лежали на прямой МК.

  2. На линии сгиба отметьте точку, лежащую на стороне МК и обозначьте её -т. V.

  3. Модель треугольника МТК перегните так, чтобы: а) линия сгиба начиналась в т. К и б) луч Т и луч М стали направленными в одну сторону и лежали на прямой МТ.

  4. На линии сгиба отметьте точку, лежащую на стороне МТ и обозначьте её –т. L.

  5. Модель треугольника МТК перегните так, чтобы: а) линия сгиба начиналась в т. М и б) луч Т и луч К стали направленными в одну сторону и лежали на прямой КТ.

  6. На линии сгиба отметьте точку, лежащую на стороне ТК и обозначьте её –т. W.


Сделайте вывод (о том, как называются отрезки TV , KL, MW и о том, как они пересекаются в треугольнике.)
Общий вывод по проделанной работе

( о том, в каком случае может быть применён способ построения медианы, биссектрисы и высоты треугольника путём перегибания модели треугольника

и о том, в чём недостатки и преимущества этого способа по сравнению с традиционным способом построения медианы, биссектрисы и высоты треугольника с помощью чертежного инструмента.)

Практическая работа в 8 классе

«Построение прямого угла с помощью нити длиной 12 единиц»

Цель: овладение навыками построения прямоугольного треугольника со сторонами 3, 4 и 5 единиц с помощью нити.

Оборудование: нить (или шнур, или тонкая верёвка), альбомный лист, ножницы, степлер (или клей, или пластилин), карандаш, масштабная линейка (или измерительный метр), маркер, чертёжный угольник.

Опорные знания: знание теоремы Пифагора, свойств египетского треугольника.

Гипотеза( о том, каким будет построение абсолютно точным или нет, а если нет, то по каким причинам)

Ход работы

  1. Взять толстую нить ( или шнур, или тонкую верёвку) длиной чуть больше 12 единиц.

  2. Связать концы нити так, чтобы длина сдвоенной нити была точно ровна 6 единицам

  3. Осторожно обрезать излишки нити после узла.

  4. Разделить с помощью масштабной линейки нить на 12 равных частей, поставив на ней точки маркером.

  5. Узел нити прикрепить к листу степлером и обозначить его карандашом на листе буквой А.

  6. Отложить от узла нити отрезок длиной 5 единиц( 5 частей нити).

  7. В конце этого отрезка поставить точку В на листе карандашом.

  8. Натянуть нить от узла А до точки В и в точке В нить прикрепить к листу степлером.

  9. Натянуть нить от узла так, чтобы длина второго отрезка стала равна 4 единицам, т.е. 4-ём частям нити ( и чтобы этот отрезок не лежал на отрезке в 5 единиц).

  10. В конце второго отрезка поставить точку С карандашом на листе.

11.В точке С прикрепить нить к листу степлером.

12. Проверить правильность построения прямого угла с помощью чертёжного угольника.
Сделайте вывод( о том, чему научились во время выполнения практической работы и от чего зависит точность построения)

Домашняя практическая работа

«Вычисление площади квартиры».

Цель: научиться применять математические знания в обыденной жизни, используя формулы нахождения площади прямоугольника и квадрата и обобщать результаты своей работы.

Оборудование: измерительная рулетка, микрокалькулятор, справочные таблицы.

Ход работы:

Вычисление площадь комнаты.

  1. Измеряю длину комнаты: а=

  2. Измеряю ширину комнаты: в=

  3. Вычисляю площадь комнаты по формуле s=

  4. Перевожу единицы площади в квадратные метры S=

  5. Округляю результат до десятых долей S=

  6. Записываю ответ:

Вычисление площади другой комнаты и кухни( по тому же алгоритму).

Нахождение площади квартиры.

  1. Складываю площади всех комнат.

  2. Оцениваю полученный результат.

  3. Сравниваю результат с известными данными.

  4. Если допускаю ошибки – исправляю их.

  5. Записываю ответ.

Вывод по проделанной работе:

Карточки-подсказки для учащихся, испытывающих затруднения.

Цель: научиться применять…………………………………………………..в обыденной жизни, используя……………………………….нахождения площади…………………………….. и …………………….

и обобщать……………………….своей работы и проверить……………………….
_________________________________________________________________
1. Решите уравнение: х2 + 3х - 10 = 0 и сравните сумму и произведение корней с коэффициентами.

2. Найдите сумму и произведение корней квадратных уравнений: а) х2– 5х + 6 = 0;

б) х2+2х - 80 = 0;

3. Проверьте с помощью теоремы Виета: верно ли найдены корни квадратного уравнения:

х2 – 15х – 16 = 0 х1 = - 1; х2 = 16

__________________________________________________________________
1. Решите уравнение: -2х2 + 8х + 3 = 0 и сравните сумму и произведение корней с коэффициентами.

2. Найдите сумму и произведение корней квадратных уравнений: а) 3х2 – 4х – 2 = 0;

б) 6х2 – 5х = 0.

3. Проверьте с помощью теоремы Виета: верно ли найдены корни квадратного уравнения: )

2х2 – 3х + 1 = 0 х1 = 1/2; х2 = 1.

4. Сформулируйте теорему, обратную теореме Виета.

Найдите с помощью теоремы, обратной теореме Виета корни квадратного уравнения:

а) х2 + 11х – 12 = 0; б) 2 х2 + 9х + 8 = 0; в) -3х2 – 6х = 0; г) х2 – 6 = 0.

_________________________________________________________________
Определите на глаз длину и высоту двери, высоту и длину окна, высоту и длину шкафа, проверить свои предположения измерениями, найти ошибки и результаты занести в таблицу:



Отрезки
Размер на глаз
Результат измерения
Ошибка

Длина двери









Высота двери









Длина окна









Высота окна









Длина шкафа









Высота шкафа









_________________________________________________________________


  1. Как будет меняться длина окружности при увеличении( уменьшении) радиуса в несколько раз?

  2. Будет ли одинаковым отношение длины окружности к её диаметру для окружностей разного радиуса?

  3. Какому целому числу примерно будет равно это отношение?

_________________________________________________________________


  1. Гипотеза: длина окружности больше её радиуса примерно в ……. раз.

  2. Гипотеза: (О том, как меняется длина окружности в зависимости от радиуса : если радиус увеличился (уменьшился) в k раз, то длина окружности………………в ………..раз)




  • Провожу и измеряю радиус 1-ой окружности (в мм): R1 =

  • Вычисляю по формуле C1 = -------- длину 1-ой окружности , округлив значение числа «пи» до десятых:

  • Записываю решение:

  • Записываю ответ:



_____________________________________________________________
Вывод-1: ( о том, как меняется длина окружности в зависимости от радиуса ( если радиус увеличился (уменьшился) в ….. раз, то длина окружности……………… )

Вывод- 2: (выявляю закономерность: длина окружности больше её радиуса примерно в … раз)

Вывод по окончании работы: (о том чему научился на практической работе и как найти длину окружности и площадь круга, зная радиус).

_______________________________________________________________
Общий вывод по проделанной работе

( о том, в каком случае может быть применён способ построения медианы, биссектрисы и высоты треугольника путём перегибания модели треугольника

и о том, в чём недостатки и преимущества этого способа по сравнению с традиционным способом построения медианы, биссектрисы и высоты треугольника с помощью чертежного инструмента.)

________________________________________________________________

Литература.

Математика: Учебник для 5 класса общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. 5-е изд. — М.: Мнемозина, 2009.
Математика: Учебник для 6 класса общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. 5-е изд. — М.: Мнемозина, 2009.
Алгебра. 7 класс: Учебник для 7 класса общеобразовательных учреждений/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др. – М.: Просвещение, 2009.

Алгебра. 8 класс: Учебник для 7 класса общеобразовательных учреждений/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др. – М.: Просвещение, 2009.

Алгебра. 9 класс: Учебник для 7 класса общеобразовательных учреждений/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др. – М.: Просвещение, 2009.

Геометрия, 7 – 9 классы : Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.– М.: Просвещение, 2011.

Изучение геометрии в 7, 8, 9 классах: Метод. рекомендации к учеб.: Кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др.– М.: Просвещение, 2009.

Саранцев, Г. Современный урок математики // Математика в школе.– 2006.– № 7.– С. 50
1   2   3