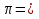«Усиление практической направленности математики через организацию систематического проведения практических и лабораторных работ»
 Скачать 442.46 Kb. Скачать 442.46 Kb.
|
Содержание. Условия возникновения П.О. …………………………………………………..3 Актуальность П. О. ………………………………………………………..…..5 Теоретическая база………………………………………………………..……8 Ведущая педагогическая идея……………………………………………..…14 Новизна П.О. ……………………………………………………………....…..15 Технология П.О. …………………………………………………………..….16 Приложение………………………………………………………………...…..30 Литература…………………………………………………………………..…43 Скажи мне, и я забуду, покажи мне, и я запомню, дай мне действовать самому, и я научусь. Условия возникновения ПО. Выбор данной тем обусловлен тем, что использование лабораторных работ на уроках математики не является обыденностью. Мы привыкли, что лабораторные работы широко применяются на уроках физики, химии, биологии, создается множество рабочих тетрадей и пособий с такими работами, но использованию лабораторных на уроках математики такого внимания не уделяется. Последнее время вопросу совершенствования преподавания математики уделяется большое внимание. Разрабатываются новые, более эффективные методы преподавания математики, совершенствуются формы организации уроков. Важное условие совершенствования преподавания математики — усиление ее практической направленности. Существенную роль в повышении эффективности обучения школьников играет сформированность у них практических умений и навыков, которые необходимы как для изучения математики, так и для повседневной деятельности. Лабораторные и практические работы как раз и являются одной из форм обучения математике, способствующих развитию ценных графических и вычислительных навыков и умений, необходимых для конструирования и практической деятельности. Однако, в современной школе эти работы, как правило, выполняются не систематически, а от случая к случаю. Причиной этого является недооценка учителями математики данного вида деятельности. Между тем, хочется отметить, что лабораторные и практические работы имеют большое воспитательное и образовательное значение. Они позволяют полнее и более осознано уяснить математические зависимости между величинами; ознакомиться с измерительными и вычислительными инструментами и их применением на практике; установить более тесные связи между различными разделами курса математики и между различными школьными курсами. Актуальность ПО. В новых Федеральных государственных общеобразовательных стандартах сказано, что в результате изучения всех школьных предметов у учащихся должны быть развиты личностные, регулятивные, коммуникативные и познавательные универсальные учебные действия, составляющие основы формирования способности к освоению систематических знаний, их самостоятельному пополнению, переносу и интеграции, способности к сотрудничеству и коммуникации, решению личностно и социально значимых проблем и воплощению решений в практику, способности к самореализации, саморегуляции и рефлексии, к целеполаганию, самостоятельной постановке новых учебных задач и проектированию собственной учебной деятельности. Обучающимся будут предъявлены учебно-практические задачи, направленные на формирование и оценку навыка разрешения проблем, навыка сотрудничества, требующие совместной работы в парах или группах с распределением ролей и разделением ответственности за конечный результат. В основе реализации основной образовательной программы и решения этих задач будет лежать системно - деятельностный подход. Осуществить постепенный переход к новым ФГОСам как раз, и помогают лабораторные и практические работы, так как они формируют деятельностные умения учащихся, формируют навыки исследовательской работы, навыки сотрудничества в парах или группах. Приобретённые навыки во время выполнения таких работ позволяют успешно решать практико-ориентированные задачи на ГИА и ЕГЭ. При выполнении практических и лабораторных работ ученики проводят мини исследования, т.е. приобщаются к исследовательской деятельности: выдвигают гипотезу, анализируют связи между величинами, проводят сравнение и проверяют гипотезу, учатся делать выводы и проводить рефлексию. Применение в учебной деятельности таких работ учит применять полученные знания на практике и в обыденной жизни, развивает познавательный интерес к предмету, разнообразит учебный процесс, доказывает значимость математических знаний на практике, т.е.преподносит математику ни как отвлечённую от повседневной жизни науку, а как прикладную науку для решения жизненно важных задач. Проведение лабораторных и практических работ с учащимися вносит разнообразие в уроки математики; повышает активность и самостоятельность учащихся на уроке; способствуют повышению качества знаний учащихся по математике; делает абстрактные теоретические положения понятными, доступными, наглядными. При правильной организации работ воспитывается культура труда (умение организовать рабочее место, содержать его и инструменты в порядке), привычка к систематическому труду, стремление к познанию и постоянному совершенствованию полученных знаний и навыков. Изящно выполненная работа способствует развитию чувства красоты, удовлетворенности от проделанной работы. Цель моей работы – изучение влияния методических приемов проведения практических и лабораторных работ на формирование практических умений и навыков у школьников на уроках математики. Задачи:
Объект исследования – процесс формирования практических умений и навыков у школьников на уроках математики Предмет исследования – практические и лабораторные работы, способствующие эффективному формированию практических умений и навыков на уроках математики. Теоретическая база. История применения лабораторных и практических работ в советской школе. В массовой практике обучения лабораторные работы по физике и химии стали применяться в учебном процессе реальных училищ с 1906 года. В последующие годы передовые учителя стали проводить лабораторные работы по математике. Так в книгах того времени, например, Л.В. Глаголевой, дано описание 80 лабораторным работам по арифметике, в книгах Гуревича В. приведено около 4000 заданий к лабораторным работам по геометрии. Вопрос о лабораторных работах был предметом постоянного обсуждения на съездах учителей. Проблеме организации лабораторных работ как по предметам естественнонаучного цикла, так и по математике уделялось большое внимание. В послевоенные годы жизнь советской школы также характеризуется творческой работой учителей. Вопрос о необходимости проведения лабораторных работ не оставался без внимания. Проблеме лабораторных работ уделялось большое внимание специалистами в области частных методик. Ими рассматривались терминологические вопросы, вопросы, связанные с содержанием лабораторных работ. В периодической печати постоянно присутствовали статьи об опыте организации лабораторных работ. Авторы этих статей, рассказывая о своей учительской практике, рассматривали важные теоретические вопросы:
На данный же момент лабораторным работам по математике не уделяется такого внимания. Хотя их использование эффективно в достижении различных целей обучения математики. Одной из проблем современной методики преподавания математики является реализация связи обучения с жизнью. Всем известно, что знать и уметь не одно и то же. Названная проблема далеко не нова. Еще в 1958 г. был принят «Закон об укреплении связи школы с жизнью и о дальнейшем развитии системы народного образования в СССР». В соответствии с законом в программу и действующие учебники по математике были внесены изменения, которые касались, главным образом, укрепления вычислительных и измерительных навыков. Эти изменения, безусловно, благоприятно сказались на усилении интереса учащихся к предмету, так как приближенные вычисления, решение производственно-технических задач, выполнение различных хозяйственных расчетов, использование измерительных инструментов и т.п. разнообразили содержание школьной математики и создали условия для понимания школьниками значения математики в жизни. Однако до сих пор недостаточно уделяется внимания тому, чтобы научить учащихся использовать полученные знания на практике. Суть понятий «лабораторная работа» и «практическая работа». Лабораторные работы по математике – самостоятельное решение учащимися задач, условия которых задаются конкретными техническими деталями, различными предметами или специально для этого изготовленными моделями, чертежами для достижения определенных учебных целей, в частности для выработки у учащихся умений и навыков применения на практике полученных математических знаний. Лабораторная работа – это такой метод обучения, при котором учащиеся под руководством учителя и по заранее намеченному плану проделывают опыты или выполняют определенные практические задания и в процессе их воспринимают и осмысливают новый учебный материал, закрепляют полученные ранее знания. Таким образом, можно сделать вывод, что лабораторная работа может выступать и в качестве метода, и в качестве формы, и в качестве средства обучения. Введение лабораторных работ по математике не противопоставляется проведению практических работ. Практические работы – это те самостоятельные работы учащихся, целью выполнения которых является поверка теоретически установленных фактов, соотношений, зависимостей в отдельном конкретном случае, применение теоретических знаний на практике, решение практических задач. Лабораторные работы не могут заменить непосредственно практические работы. Наоборот, первые обеспечивают хорошую подготовку для проведения последних. При выполнении практических работ математическая теория ближе к практике, а потому с педагогической точки зрения ценнее . Вот почему проведение практических работ по математике должно быть совершенно обязательным в каждом классе. Лабораторные же работы – это необходимый подготовительный этап к проведению непосредственно практических работ. Классификация лабораторных и практических работ. Необходимо проводить разнообразные лабораторные и практические работы не только по содержанию, но и по их ведущей учебной целевой направленности. Их можно классифицировать следующим образом: установочные, проводимые с целью ознакомления учащихся с оборудованием и простейшими приемами работы с ним; иллюстративные, которые знакомят учащихся с отдельными фигурами, их свойствами; тренировочные, предназначенные для закрепления изученных свойств, соотношений; исследовательские, направленные на практический поиск новых свойств, которые затем будут логически обоснованы; творческие, связанные с конструированием на основе геометрических свойств специальных приборов; обобщающие, основной целью которых является систематизация и обобщение теоретических знаний, методов построений, изображений, измерений. Цели использования лабораторных и практических работ в обучении математике. Использование лабораторных и практических работ при обучении математике помогут достичь следующих целей:
Примерный план проведения лабораторных и практических работ. 1. Учитель сообщает тему работы заранее. Организует повторение ранее изученного материала, необходимых понятий, формул, определений, которые придётся использовать при выполнении работы. 2. На уроке ставится цель работы. Каждый обучающийся знакомится с инструкцией, с содержанием и описанием выполняемой работы, даётся минимально необходимый инструктаж (этапы работы, последовательность выполнения измерений и вычислений, схема оформления работы и т. д.). 3. Работа выполняется каждым учащимся самостоятельно или в группах. К выполнению расчётов он приступает после тщательного выполнения измерений. Результаты измерений могут заноситься в определённую таблицу. 4. Учитель, наблюдая за работой учащихся, проверяет решения, указывает на индивидуальные и общие ошибки учащихся. Особое внимание уделяется менее подготовленным учащимся. 5. В конце занятия отводится несколько минут для подведения итогов работы. При необходимости, если работу выполняет группа, то проводится защита работы. При оценке качества выполнения работ учитель должен учитывать рациональность выбора величин, подлежащих измерению, применение рациональных вычислений, умение правильно выполнять приближённые вычисления, оформление работы и ответы на контрольные вопросы. При групповой работе к критериям оценки результатов учащихся добавляются ещё и уровни развития коммуникативных и адаптивных качеств, умения работать в сотрудничестве, принимать чужое мнение, противостоять трудностям. 6. На одном из следующих занятий проводится подробный анализ выполненной работы: сравнение и обсуждение полученных результатов, разбираются типичные ошибки. (Обычно за выполнение таких работ неудовлетворительных оценок у ребят не бывает). Лабораторные и практические работы как средство осуществления связи теории с практикой. Важное значение в реализации связи теории с практикой при обучении математике имеют лабораторные и практические работы. Под такими работами понимают учебные занятия, которые решаются конструктивными методами с применением непосредственных измерений, построений, изображений, геометрического моделирования и конструирования. В результате чего происходит совершенствование навыков. Поэтому система лабораторных и практических работ направлена на развитие конструктивных умений и навыков учащихся. Практические и лабораторные работы по каждой теме не должны быть изолированы друг от друга. Они должны быть тесно связаны с проблемным материалом, способствовать решению главных образовательных, воспитательных и развивающих целей, предусмотренных программой. Данные работы должны учитывать индивидуальные особенности каждого ученика, в частности уровень их подготовки, способности и работоспособности. В процессе выполнения лабораторных и практических работ учащиеся должны научиться пользоваться как можно большим числом различных инструментов (масштабная линейка, мерная лента, транспортир, палетка, штангенциркуль и т.д.), различных вычислительных средств. Очень важно научить учащихся самостоятельно определять, какой инструмент и вычислительное средство надо применить при выполнении той или иной работы. По содержанию все работы должны иметь практическую направленность, способствовать выработке у учащихся практически важных умений и навыков, которые они могли бы использовать на уроках технологии, при изучении таких учебных предметов как черчение, химия, физика, география, в быту, при продолжении общего или получении профессионального образования. Ведущая педагогическая идея. Ведущая педагогическая идея опыта заключается в том, что формирование и развитие практических умений и навыков во время выполнения практических и лабораторных работ позволяет добиться более высокого уровня умения оперировать знаниями, получаемыми на уроках математики в решении задач практического характера и умения осуществлять подход к изучению явлений, протекающих в различных жизненных ситуациях. А также проведение практических и лабораторных работ позволяет осуществить связь между различными школьными курсами. Новизна ПО. Новым является то, что последний год стала проводить лабораторные работы исследовательского характера, формирующие у учеников навыки исследовательской деятельности и то, что при проведении лабораторных и практических работ реализую системно - деятельностный подход к обучению школьников, который определяется новыми ФГОСами. Технология ПО. Для формулировки цели, гипотезы и вывода учащимися на практических и лабораторных работах использую следующие приёмы: -даю систему опорных вопросов, т.е. провожу актуализацию знаний; -даю карточки-подсказки с пропущенными словами или числами или с пропущенной частью формулы; -пишу в инструкции, о чём должна быть цель, гипотеза или вывод; - использую карточки с дополнительными заданиями; -перед выдвижением гипотезы даю предварительные задания по пройденным темам, проанализировав результаты которых можно вывести связь между рассматриваемыми величинами; - перед выдвижением гипотезы задаю проблемный вопрос; -при подведении итога урок, на котором выполнялась практическая или лабораторная работа использую приёмы: «синквейн», «лестница достижений», «балльная система оценивания» как способы проведения рефлексии. На первых лабораторных и практических работах в 5 классе работа идёт по инструкции, которую даёт учитель. Инструкция содержит лишь этапы: тема, цель, оборудование, ход работы и вывод. Причём первые 3 этапа уже написаны. Ученики лишь заполняют ход работы по готовому алгоритму и записывают вывод, исходя из цели работы. На практической работе по теме « Вычисление длины окружности и площади круга» в 6 классе предлагаю выполнить работу по готовому алгоритму. В начале урока предлагаю детям систему вопросов, т.е. провожу актуализацию знаний.
Цель и оборудование пишу в инструкции сама. Если работа обучающая цель должна начинаться со слов: я научусь… (или научиться) Цель: научиться находить длину окружности и площадь круга по формулам, выполнив необходимые измерения и расчеты и обобщать результаты своей работы. Оборудование: 3 модели круга разного радиуса, циркуль, масштабная линейка, нитка, ножницы, клей-карандаш. Затем ученики выдвигают гипотезу. Чтобы они смогли это сделать, использую следующие приёмы. Пишу в инструкции, о чём должна быть гипотеза. Например:Гипотеза: (О количественной связи длины окружности и её радиуса), а более слабым ученикам раздаю карточки-подсказки с пропущенными словами или числами: Гипотеза: длина окружности больше её радиуса примерно в ……. раз. Гипотеза: (О том, как меняется длина окружности в зависимости от радиуса : если радиус увеличился (уменьшился) в k раз, то длина окружности………………в ………..раз) Затем ученикам раздаю инструкции для выполнения работы, и ученики, используя её, записывают в тетради ход работы, выполнив необходимые измерения и написав необходимые расчётные формулы. В алгоритме выполнения работы использую систему незаконченных предложений (в которых, например, нужно дописать правую часть формулы). Например:
Затем ученики проверяют гипотезу, анализируя результаты. В конце урока предлагаю ученикам обобщить результаты работы. На этом этапе применяю дифференцированный подход. Более мотивированным ученикам предлагаю сделать выводы самим. А слабым ученикам даю карточки-подсказки с пропущенными словами или указываю в инструкции, о чём должен быть сделан вывод. Например: |