«Усиление практической направленности математики через организацию систематического проведения практических и лабораторных работ»
 Скачать 442.46 Kb. Скачать 442.46 Kb.
|
Вывод-1: ( о том, как меняется длина окружности в зависимости от радиуса ( если радиус увеличился (уменьшился) в ….. раз, то длина окружности……………… ) Вывод- 2: (выявляю закономерность: длина окружности больше её радиуса примерно в … раз) Вывод по окончании работы: (о том чему научился на практической работе и как найти длину окружности и площадь круга, зная радиус). А если практическую или лабораторную работу дети выполняют индивидуально, то составляю дифференцированные инструкции с заданиями разной степени сложности. Так, например, на практической работе по алгебре в 8 классе «Теорема Виета» перед началом работы провожу актуализацию знаний: предлагаю повторить: а) понятия полного и приведённого квадратного уравнения; б) общий вид квадратного трёхчлена; в) алгоритм решения квадратных уравнений; г) формулы для нахождения дискриминанта и для нахождения корней. Затем предлагаю ученикам, имеющим «3» по математике, решить два приведённых квадратных уравнения и результаты занести в таблицу:
А после сравнить сумму и произведение корней каждого из уравнений с его коэффициентами. Затем ученикам предлагаю выдвинутьгипотезуо связи корней приведённого квадратного уравнения и его коэффициентов и записать её символами. А ученикам, занимающимся на «4 и 5» предлагаю решить два полных квадратных уравнения и результаты занести в таблицу:
А затем предлагаю сравнить сумму и произведение корней каждого из уравнений с его коэффициентами и выдвинуть гипотезу о связи корней полного квадратного уравнения и его коэффициентов и записать её символами. Затем предлагаю проверить гипотезу. Одной группе учеников предлагаю придумать приведенное квадратное уравнение, а другой группе - полное квадратное уравнение и найти сумму корней квадратного уравнения и произведение корней квадратного уравнения. Затем предлагаю каждой группе обобщить результаты работы и записать вывод, отразив в нём словами связь корней квадратного уравнения и его коэффициентов. Затем предлагаю проверить свои выводы. Ученикам, имеющим «3» по математике, предлагаю карточки с дополнительными заданиями: 1. Решите уравнение: х2 + 3х - 10 = 0 и сравните сумму и произведение корней с коэффициентами. 2. Найдите сумму и произведение корней квадратных уравнений: а) х2– 5х + 6 = 0; б) х2+2х - 80 = 0; 3. Проверьте с помощью теоремы Виета: верно ли найдены корни квадратного уравнения: х2 – 15х – 16 = 0 х1 = - 1; х2 = 16. А ученикам, успевающим на «4» и «5», предлагаю карточки со следующими дополнительными заданиями: 1. Решите уравнение: -2х2 + 8х + 3 = 0 и сравните сумму и произведение корней с коэффициентами. 2. Найдите сумму и произведение корней квадратных уравнений: а) 3х2 – 4х – 2 = 0; б) 6х2 – 5х = 0. 3. Проверьте с помощью теоремы Виета: верно ли найдены корни квадратного уравнения: ) 2х2 – 3х + 1 = 0 х1 = 1/2; х2 = 1. 4. Сформулируйте теорему, обратную теореме Виета. Найдите с помощью теоремы, обратной теореме Виета корни квадратного уравнения: а) х2 + 11х – 12 = 0; б) 2 х2 + 9х + 8 = 0; в) -3х2 – 6х = 0; г) х2 – 6 = 0. Также предлагаю своим ученикам выполнить домашние практические работы: «Вычисление площади квартиры», «Развитие глазомера в домашних условиях», «Составление плана квартиры». Домашнюю практическую работу: Вычисление площади квартиры предлагаю выполнить после классной практической работы «Вычисление периметра и площади прямоугольника и квадрата», при выполнении которой ученики приобрели необходимые умения и навыки. Цель для этих работ ребята формулируют в классе с помощью учителя в ходе обсуждения различных формулировок. Чтобы она была сформулирована более точно даю детям карточки с пропущенными словами. Например, Цель: научиться применять…………………………………………………..в обыденной жизни, используя……………………………….нахождения площади…………………………….. и ……………………. и обобщать……………………….своей работы и проверить………………………. Предлагаю дома сформулировать гипотезу о количественном значении площади, т.е. оценить предполагаемый результат на глаз( не узнавая значение площади у родителей), а выполнив необходимые измерения и вычисления( округлив результат до десятых долей), узнать, насколько они ошиблись, т.е. проверить гипотезу. Гипотеза: думаю, что площадь квартиры равна……………… А оборудование и ход работы предлагаю записать дома самостоятельно, а также сделать вывод о том, чему научились при выполнении работы. Анализируя выполнение домашней практической работы, спрашиваю детей о том, с какими трудностями они столкнулись и как их преодолели. Домашнюю практическую работу: «Развитие глазомера в домашних условиях», предлагаю выполнить после классной практической работы «Метрическая система мер»: Определить на глаз длину и высоту двери, высоту и длину окна, высоту и длину шкафа, проверить свои предположения измерениями, найти ошибки и результаты занести в таблицу:
Для формулировки цели предлагаю вставить в предложение пропущенные слова Цель: развитие………………и овладение навыками…………………… По окончании работы предлагаю сделать вывод, о том насколько улучшился( или не улучшился) глазомер. Домашнюю практическую работу «Составление плана квартиры» предлагаю выполнить после классной практической работы «Масштаб». А если работа носит исследовательский характер, то сообщаю ученикам лишь тему, а цель, гипотезу, ход работы и вывод предлагаю ученикам написать самим. Например, при выполнении работы «Число π» сначала провожу актуализацию знаний, предлагаю ответить на вопросы: -С помощью какого чертёжного инструмента можно построить окружность заданного радиуса? -Какая геометрическая фигура называется окружностью? -Какой отрезок называется а)радиусом, б) диаметром окружности? -Как можно найти длину окружности, не зная расчётной формулы? - Что называется отношением двух чисел? Проведя актуализацию знаний, задаю ученикам проблемный вопрос, который записываю на доске: У окружностей разного радиуса значение отношения длины окружности к её диаметру будет одинаковым или будет увеличиваться с увеличением радиуса, или будет уменьшаться при увеличении радиуса? Дети высказывают разные мнения (идёт «столкновение мнений»). Происходит выдвижение гипотезы. Предлагаю записать гипотезу в тетрадь для практических и лабораторных работ. (Предположения детей могут быть неверными, а затем в ходе исследования могут быть опровергнуты или подтверждены). Ученики выдвинули две гипотезы: -отношение длины окружности к её диаметру будет увеличиваться с увеличением радиуса, -отношения длины окружности к её диаметру будет одинаковым при увеличении радиуса. Для того , чтобы ученики могли поставить цель, учитывая выдвинутую гипотезу, выписываю на доске несколько глаголов, с которых может начинаться формулировка цели: доказать, найти, обосновать, разработать, выяснить, определить, установить. Учениками были поставлены цели: - доказать, что с увеличением радиуса окружности отношение длины окружности к её диаметру будет увеличиваться; -разработать план, по которому сможем найти отношение длины окружности к её диаметру для окружностей разного радиуса и сравнить результаты, - установить, каким будет отношение длины окружности к её диаметру для окружностей разного радиуса. ( Можно было поставить цель:Объяснить, почему, для окружностей разного радиуса значение отношения длины окружности к её диаметру будет одинаковым.) В зависимости от поставленной цели ученики объединились в группы. Затем записали оборудование ( например: циркуль, масштабная линейка, нитка, ножницы, клей- карандаш) и приступили к ходу работы. Ученикам, испытывающим затруднения даюкарточки-подсказки, например: Чтобы найти отношение двух величин, нужно значение одной величины разделить на значение другой величины. В ходе работы одна из групп составила следующий план своих действий:
И затем на основе цели записали вывод: мы разработали план, по которому сможем найти отношение длины окружности к её диаметру для окружностей разного радиуса и сравнить значения отношений. Вывод у другой группы: мы установили, что отношение длины окружности к её диаметру для окружностей разного радиуса будет одинаковым. А третья группа в ходе работы своей цели не достигла ( при проверке гипотезы, анализируя результаты, поняли, что выдвинули неверную гипотезу) и тогда делают вывод, что цель поставили неправильно. Но это не означает, что они ничему не научились при выполнении работы. Они провели исследование, т.е. приобрели навыки исследовательской работы, отрабатывали вычислительные навыки, научились сравнивать и анализировать. В группах ученики обмениваются мнениями, происходит обсуждение формулировки вывода. В ходе обсуждения дети находят ошибки в формулировке друг друга, корректируют её и записывают уже уточнённую. Сравнивают полученные результаты с выдвинутой гипотезой, анализируют итог, к которому пришли (т. е. учатся элементам исследовательской деятельности: сравнению и анализу.) Затем ученикам говорю о том, что они в основном сделали правильный вывод, что отношение длины окружности к длине её диаметра является одним и тем же числом и что это число обозначают буквой π и предлагаю записать формулу длины окружности. На этапе рефлексии предлагаю ученикам выбрать формулу из записанных на доске, соответствующую выводу, к которому пришли в ходе выполнения работы: 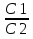 = =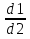 ; ; 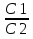 = =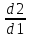 ; ; 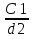 = =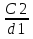 ; ; 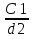 = =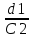 И задаю вопрос: На уроках по какому предмету используется зависимость длины окружности и её диаметра(или радиуса) и с какой целью? Если не отвечают сразу, подсказываю, что на уроках технологии ( обслуживающего труда). Тогда девочки класса вспоминают, что используют формулу для нахождения длины окружности, когда делают выкройки (например, круглого воротника или юбки «солнце-клёш»). Измеряя с помощью измерительной ленты, например, обхват шеи – получают значение длины окружности, учитывая это значение и зная формулу длины окружности, вычисляют её радиус, а затем с помощью циркуля проводят полуокружность( или четвёртую часть окружности). На этом примере прослеживается применение математических знаний в повседневной жизни, т.е. доказывается применение математики в жизненных ситуациях – что отвечает требованиям новых ФГОС. Затем предлагаю учителям ознакомиться с разработанными мною инструкциями некоторых практических и лабораторных работ ( см. Приложение). А после знакомлю коллег с примерными критериями оценивания, которые я использую на практических и лабораторных работах. Критерии оценивания работ. Общего критерия оценивания лабораторных и практических работ нет, так как существуют различные типы работ. По одной из классификаций они подразделяются на обучающие и прикладные. Форма отчёта по практическим и лабораторным работам тоже варьируется в зависимости от их темы и назначения. Возможно, не каждую работу нужно оценивать отметкой. Какая-то небольшая по объёму работа может служить подготовкой к изучению новой темы или подвести к решению проблемы, поставленной на уроке. Есть работы прикладного характера, в которых можно применить различные формы оценивания результатов. Например, можно провести рефлексию, используя: а) цветовую систему оценивания ( карточка красного цвета – приобрёл прочный навык построения биссектрисы треугольника путем перегибания модели; зелёного – испытывал затруднения, пользовался подсказками; коричневого - не смог построить, нужно ещё тренироваться); б) словесную систему оценивания, когда ученикам предлагаю ответить на вопросы: что узнали нового, чему научились, в каких моментах испытывали затруднения; в) синквейн, развивающий критическое мышление Примеры синквейнов, составленных моими учениками на этапе рефлексии выполнения практической работы «Окружность и круг» . 1. Окружность. 2. Замкнутая, кривая. 3. Измеряем, строим, вычисляем. 4. Длину можно измерить нитью. 5. Фигура, круг, линия, длина, колесо. 1 .Круг. 2. Плоский, ровный. 3. Изучаем, рисуем, вырезаем. 4. Вычисляем площадь по формуле. 5. Радиус, диаметр, площадь, шар, диск. 1. Окружность 2. Круглая, большая 3. Рисуется, измеряется, стирается 4. Чертится с помощью циркуля 5. Фигура г) приём «рука знаний» ( обводят руку и над каждым пальчиком пишут, чему научились); д) приём «лестница достижений» (Например, для проведения рефлексии по работе «Вычисление площади квартиры» ученикам раздаю карточки с рисунком лестницы, на нижней ступеньки которой, например, написано: научился измерять длину и ширину комнаты; на следующей: научился вычислять площадь комнаты; а на верхней: научился вычислять площадь квартиры.А ученик рисует фигурку человека на соответствующей ступеньке лестницы). е) приём «плюс – минус» (интересно ли было выполнять работу); ж) балльную систему оценивания. ( оценивая в баллах те этапы работы, которые ученики выполняют самостоятельно). Например, на этапе «гипотеза» применяю шкалу от 0 до 2 баллов ( в гипотезе нужно отразить связь между корнями квадратного уравнения и его коэффициентами): 0 б – сформулирована неверно, 1 б – сформулирована неточно (частично верно), 2 б – сформулирована верно. На этапе «ход работы» применяю шкалу от 0 до 3 баллов: 0 б – все этапы алгоритма выполнены неверно, 1 б - допущены ошибки больше, чем в половине заданий, 2 б - допущены ошибки меньше, чем в половине заданий, 3 б - все этапы алгоритма выполнены верно. На этапе «вывод» применяю шкалу от 0 до 2 баллов: (В выводе требуется сформулировать полученный результат словами) 0 б – написан неверно, 1 б - написан частично верно, 2 б - написан верно. На этапе «дополнительные задания» применяю шкалу от 0 до 4 баллов: 0 б - не выполнены или выполнены неверно все 4 задания, 1 б – выполнено верно 1 задание, 2 б - выполнены верно 2 задания, 3 б - выполнены верно 3 задания, 4 б - - выполнены верно 4 задания. Затем баллы перевожу в отметку: 7 – 11 б -------------- «5», 5 – 6 б -----------------«4», 3 – 4 б ------------------«3», 2 б и меньше ---------«2». Приложение. Создание банка данных практических и лабораторных работ. Практическая работа «Вычисление периметра и площади прямоугольника и квадрата». Цель: научиться находить периметр и площадь прямоугольника и квадрата по формулам, выполнив необходимые измерения и обобщать результаты своей работы. Оборудование: модели прямоугольников и квадратов, сделанные учениками дома из цветного картона, масштабная линейка. Ход работы. (ученики обмениваются моделями прямоугольников и квадратов) Вычисление периметра и площади прямоугольника. 1. Измеряю длину прямоугольника: а= 2. Измеряю ширину прямоугольника: в= 3. Нахожу площадь прямоугольника по формуле: S= 4. Перевожу единицы площади в квадратные сантиметры. 5. Записываю ответ. 6. Вычиляю периметр прямоугольника по формуле: Р= 7 .Записываю ответ. |