Решения.
Всего 11 цветов, 6 из них – розы, следовательно, гвоздик 11-6=5. Из всех цветов 5 имеют красный цвет, а остальные – белый. Тогда наибольшее число гвоздик белого цвета мы получим, если красными будут только розы. Значит, наибольшее число белых гвоздик может быть 5. Ответ: 5
Эта задача имеет несколько решений, приведем одно из них. Первому купцу отдадим 3 полные, 1 полупустую и 3 пустых бочки; второму – 2 полные, 3 полупустые и 2 пустые бочки; третьему также 2 полные, 3 полупустые и 2 пустые бочки.
Сложим все фрукты на весы, их общий вес равен 550+450=1000 г, при этом на весах оказалось 5 персиков, 5 груш и 5 яблок. Тогда персик, груша и яблоко весят 1000:5=200 г. Ответ: 200 г
: Разница в тетрадях, которые ученик хотел приобрести, 15-11=4, а разница в рублях 5+7=12. Следовательно, каждая тетрадь стоит 12:4=3 рубля. Тогда денег у школьника было 113+5=38 рублей.
Ответ: 38 рублей
Решение: Оформим решение таблицей, в которой будем указывать, сколько литров молока в данный момент находится в каждом бидоне:
-
17 л
|
-
|
-
|
5
|
5
|
10
|
10
|
15
|
15
|
17
|
-
|
3
|
3
|
8
|
8
|
13
|
5л
|
-
|
5
|
-
|
5
|
-
|
5
|
-
|
5
|
3
|
3
|
-
|
5
|
-
|
5
|
-
|
Необходимо иметь в виду, что «лишнее» молоко мы выливаем обратно
в цистерну.
Из условия задачи ясно, что Марат живет ниже всех, а Ваня - между Петей и Катей. Следовательно, на первом этаже живет Марат, на втором – Петя, на третьем – Ваня и на четвертом – Катя.
При любом сочетании минусов и плюсов выражение 20041234567 8=2003 будет четным, поэтому оно не может быть равно нечетному числу 2003. Ответ: нельзя
Сто, миллион
Шесть котов за шесть минут съедают шесть мышей, тогда шесть котов за 1 минуту съедят в 6 раз меньше мышей, то есть одну. Таким образом, за сто минут съедят сто мышей эти же шесть котов.
Ответ: 6 котов
Я завел свои часы и запомнил, сколько времени они показывают (например, 12.00). Придя к другу и уходя от него, я оба раза посмотрел на его часы (16.00 и 17.00), а поэтому я знал, сколько времени я пробыл у него и во сколько от него ушел. Придя домой, я определил по своим часам, сколько времени я отсутствовал (например, часы показывают 14.00, т. е. отсутствовал 2 часа), а вычтя из этого времени то время, которое пробыл у друга (1 час), определил, сколько времени я потратил на путь к нему и от него (2 -1=1 час). Разделив это время пополам (полчаса) и прибавив его к последнему показанию часов друга, я определил время прибытия к себе домой (17.00+0.30=17.30).
В первой скобке уменьшаемое не должно быть больше 385. Во второй скобке делимое не может быть меньше 385. Следовательно, пропущено число 385. Ответ: 385
Это можно сделать так:

Инженер приехал на завод на 20 мин раньше обычного, т.е. машина ехала на 20 мин меньше, чем обычно. А это то время, которое ей нужно, чтобы проехать от места встречи с инженером до вокзала и обратно до места встречи. Значит, машине не хватило 10 мин, чтобы доехать до вокзала (т.е. до 8 часов). Следовательно, часы показывали 7ч 50 мин. Ответ: 7 ч 50 мин
Малыш съедает 1 банку за шесть минут, а Карлсон за шесть минут съедает две банки, тогда вместе они за шесть минут съедят 3 банки варенья. Следовательно, одну банку варенья они съедят за 6:3=2 минуты. Ответ: 2 минуты
)
Для нумерации страниц с 1 по 9 понадобится 9 цифр, для страниц 10-99 требуется 902=180 цифр, тогда на страницы с трехзначными числами было использовано 1392-9-180=1203. Следовательно, таких страниц 1203:3=401. 401 страница и еще 99 страниц, упомянутых выше, дают ответ 500 страниц. Ответ: 500 страниц
6 класс.
Пронумеруем кошек, тогда возможные комбинации их попарного взвешивания:
1и2, 1 и 3, 1 и 4, 2 и 3, 2 и 4, 3 и 4. Мы видим, что каждая кошка участвовала во
взвешиваниях по 3 раза. Следовательно, сложив массы кошек во всех
комбинациях и разделив на 3, получим нужный общий вес кошек:
(7+8+9+10+11+12):3=57:3=19 кг.
Ответ: 19 кг
Пусть первый дал одну часть монет, тогда второй – 21=2 части, третий – 32=6
частей и четвертый – 46=24 части. Все вместе дали 1+2+6+24=33 части, а это 132
монеты, т.е. на одну часть приходится 132:33=4 монеты. Следовательно третий
пожертвовал 64=24 монеты.
Ответ: 24 монеты
Велосипедист проехал треть пути быстрее, чем мотоциклист две трети пути.
Велосипедисту после остановки осталось проехать расстояние в два раза большее,
чем он проехал до остановки. Мотоциклисту осталось проехать треть расстояния
АВ и вернуться в пункт А, т.е. тоже вдвое больше, чем он уже проехал. Сле -
довательно, велосипедист будет в пункте В раньше, чем мотоциклист в пункт А.
Ответ: велосипедист приедет раньше
Будем решать задачу с конца. На последнем озере села половина гусей, которая
летела и еще полгуся, а сели все гуси, следовательно, на 7 озеро сел 1 гусь. Тогда
перед шестым озером было (1+0,5)2=3 гуся, перед пятым – (3+0,5)2=7 гусей,
перед четвертым – (7+0,5)2=15 гусей, перед третьим – (15+0,5)2=63 гуся, и,
наконец, перед первым озером летело (63+0,5)2=127 гусей.
Ответ: 127 гусей
Следует сложить шнурок вчетверо и отстричь четверть, оставшаяся часть равна
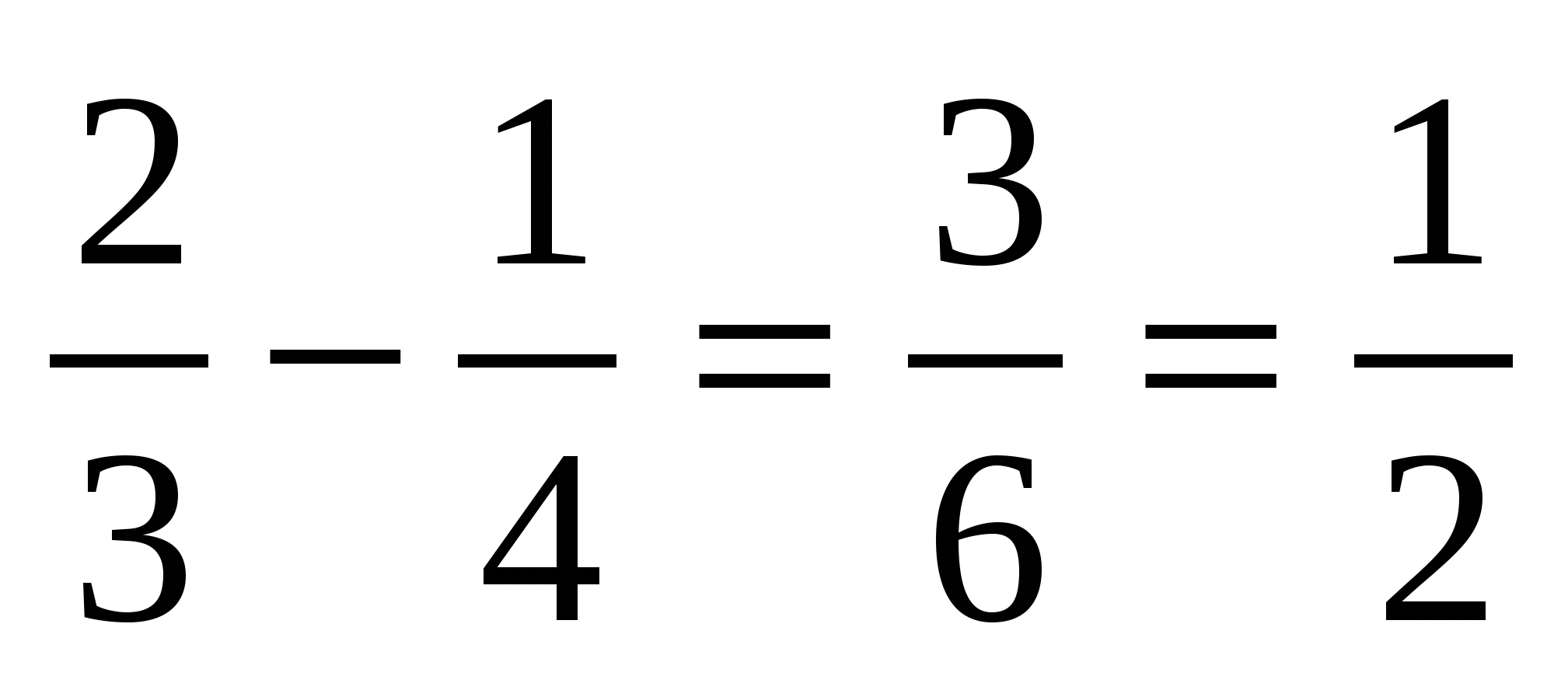 м. м.
На карточках записаны числа 5, 6, 7, 8, 9, 10 и 11. Заметим, что из них три
четных, а четыре нечетных числа. Сумма чисел на двух карточках у второго
мудреца четна, когда оба числа одинаковой четности, т.е. либо оба четные, либо оба
нечетные. Но такое заявление первый мудрец мог сделать лишь в том случае, когда
у него на трех карточках все четные числа. Значит, у него на карточках 6, 8 и 10.
Ответ: 6, 8 и 10.
В пятый день Коля поймал столько же мух, сколько за предыдущие четыре дня,
т.е. 512:2=256. За четвертый день он поймал столько мух, сколько за предыдущие
три дня, т.е. 256:2=128. Рассуждая аналогично, получим, что за третий день Коля
поймал 128:2=64 мухи, во второй и первый день – 64:2=32 мухи. Ответ: 1 день –
ухи, 2 день – 32 мухи, 3 день – 64мухи, 4 день – 128 мух, 5 день – 256 мух.
Пусть Андрей занял I место. Тогда в первом ответе первая часть – правда, а значит, вторая часть – неправда, т.е. Борис – не второй (но и не первый, т.к. первый - Андрей), а третий или четвертый. Во втором ответе первая часть – неправда, вторая часть – правда, откуда получается, что Геннадий - третий. Поэтому Борис не третий, а четвертый. Итак, Андрей – первый, Вадим – второй, Геннадий – третий, Борис – четвертый. Мог ли Андрей быть вторым? Нет, т.к. полностью был бы лжив первый ответ. Не мог Андрей быть и третьим, т.к. полностью был бы лжив второй ответ. Не мог он быть и четвертым, что следует из сопоставления 1, 2 и 3 ответов.
Ответ: Первый - Андрей, второй - Вадим, третий - Геннадий, четвертый –
Борис
Проигрывает тот, кто возьмет 35-й шар, а, следовательно, тот, кто возьмет 29-й, 23-й,
17- й, 11-й и 5-й шары. Тогда первому нужно взять четыре шарика, а затем в каждый
следующий ход дополнять до шести число шариков, взятых вторым игроком.
10. Узнаем число пассажиров в вагоне – это наибольший общий делитель чисел 418, 494 и
456. Разложив их на простые множители, получим, что в каждом вагоне ехало 219=38
пассажиров. Следовательно, вагонов было 418:38=11, 494:38=13 и 456:38=12.
Ответ: 11, 13 и 12 вагонов
11.Можно предложить такую тактику отрубания голов у Змея: 1) вначале будем отрубать по
21 голове 94 раза, т.е. отрубим 1974 головы, а 26 голов останется, новых при этом не
вырастет; 2) далее отрубим 3 раза по 17 голов, с учетом того, что вырастает по 14 голов
после каждого раза, получаем в итоге 17 голов; 3) отрубаем последним ударом 17
оставшихся голов.
12.Если в первый ящик положить 6 орехов, то это будет столько, сколько во втором и
третьем вместе. Если во второй ящик положить 10 орехов, то это столько, сколько в
первом и третьем ящиках вместе. Из этих двух предложений следует, что, сложив орехи
первого и второго ящиков плюс 16 орехов, получится то же самое количество орехов, что
в первом, втором и двух третьих ящиках вместе. Тогда в третьем ящике 16:2=8 орехов.
Ответ: 8 орехов
13.Так как a+b=2004, a и b одинаковой четности. 1) a и b - четные, тогда 7a и 3b также
четные и 7a+3b – четное и не может быть равно 6799. 2) a и b - нечетные, тогда 7a и 3b
также нечетные, но 7a+3b – четное и не может быть равно 6799. Следовательно,
7a+3b6799
Ответ: не может
14.Ответ: 235+746=981
15. Составим таблицу выигрыша:
-
2
|
10
|
12
|
20
|
Выигрыш
|
-
|
-
|
-
|
-
|
0
|
+
|
-
|
-
|
-
|
1
|
+
|
+
|
-
|
-
|
3
|
+
|
-
|
+
|
-
|
5
|
+
|
+
|
-
|
+
|
11
|
+
|
+
|
+
|
+
|
15
| |
 Скачать 491.03 Kb.
Скачать 491.03 Kb.