Другого выигрыша быть не может.
7 класс.
1.Пусть х человек на корабле было, тогда (х+30) человек стало на корабле. Количество
человек увеличилось в 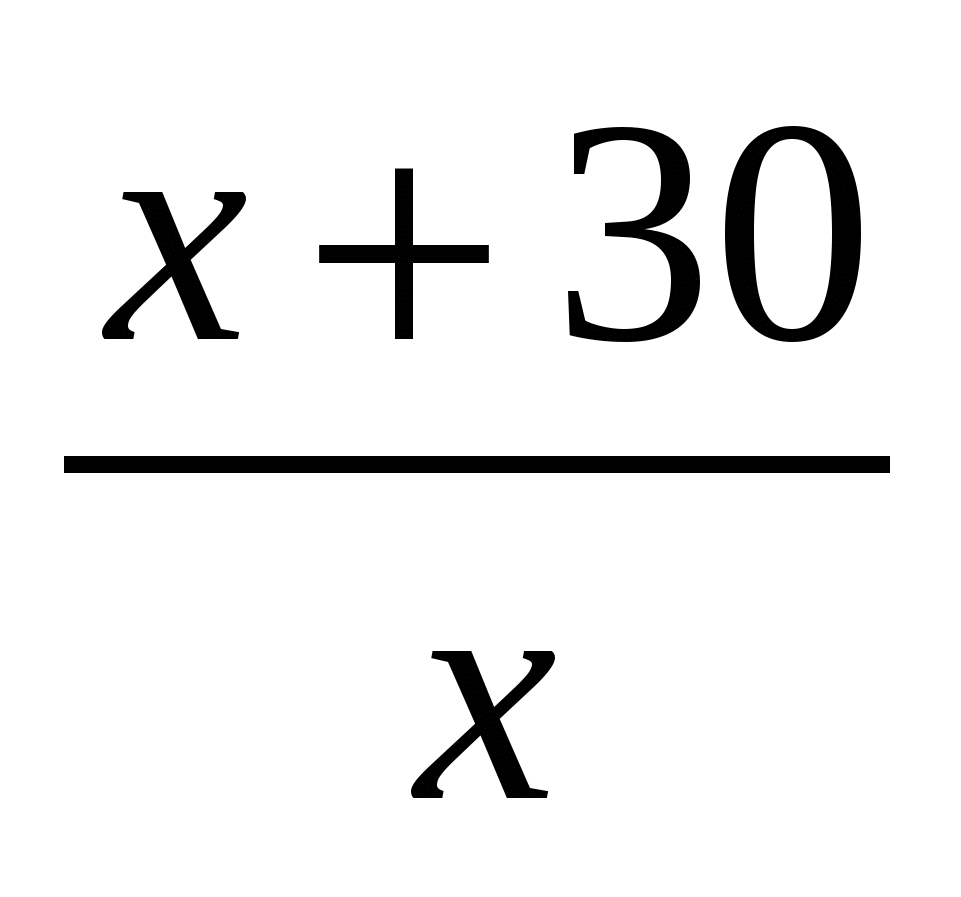 , в тоже время количество воды уменьшилось в , в тоже время количество воды уменьшилось в  раза. раза.
Составим пропорцию: 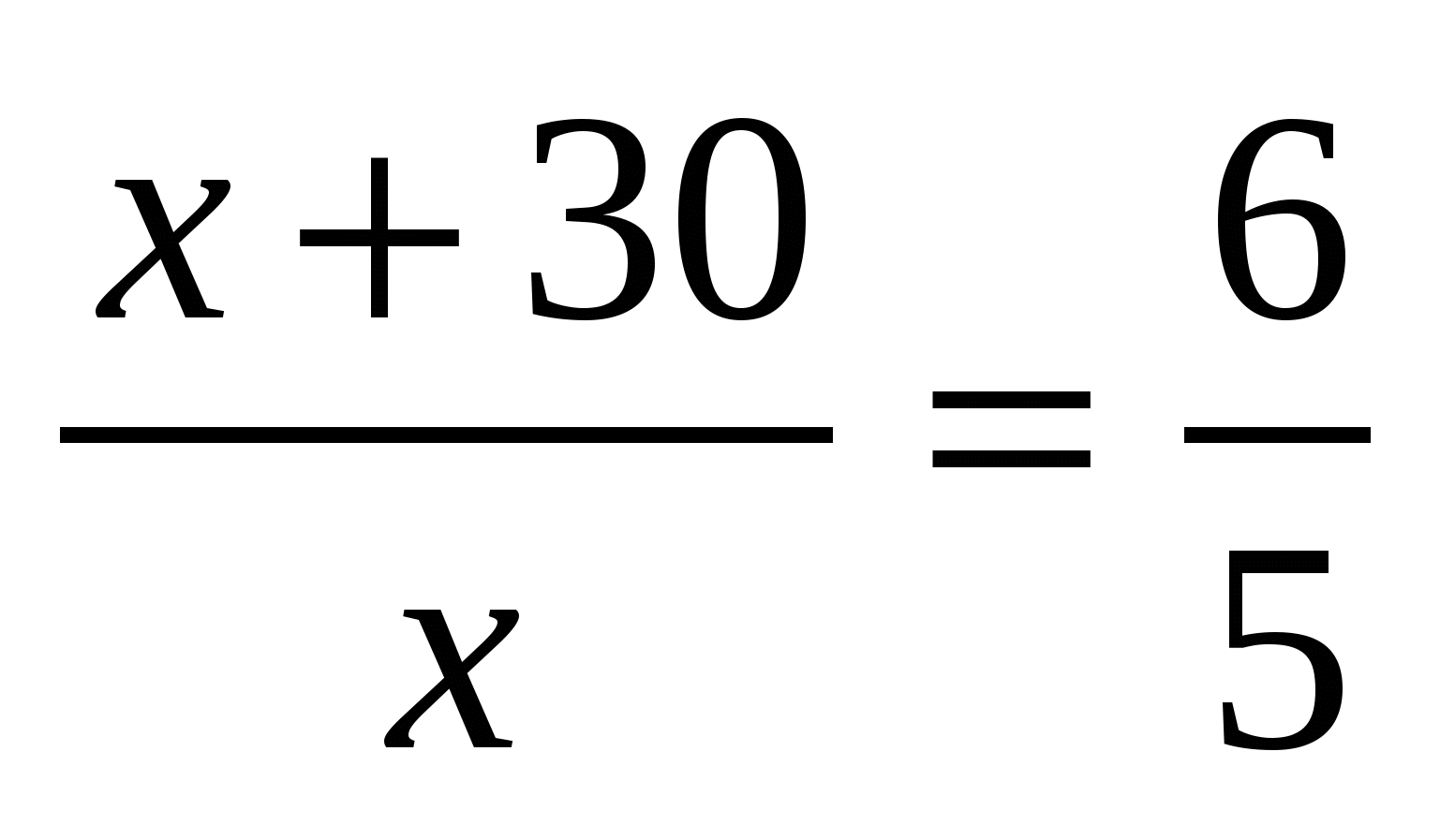 , откуда х=150. Ответ: 150 человек , откуда х=150. Ответ: 150 человек
Найдем общую сумму: 90+85+80+75=330 рублей. Заметим, что в эту сумму каждый купец вложил имеющиеся у него деньги по три раза. Следовательно, если они все сложатся, то у них будет 330:3=110 рублей. Тогда, если без первого купца получилось 90 рублей, то у первого купца 110-90=20 рублей, у второго 110-85=25 рублей, у третьего 110-80=30 рублей, у последнего 110-75=35 рублей.
Ответ: 20, 25, 30 и 35 рублей.
Можно, например так:
 может означать либо 2х (если х3), либо х+3 (если х может означать либо 2х (если х3), либо х+3 (если х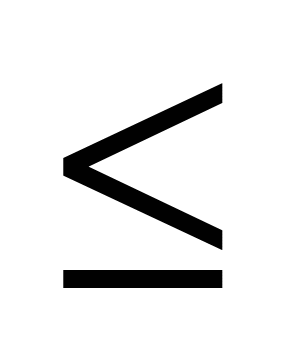 3); 3);  может означать либо 10 (если х может означать либо 10 (если х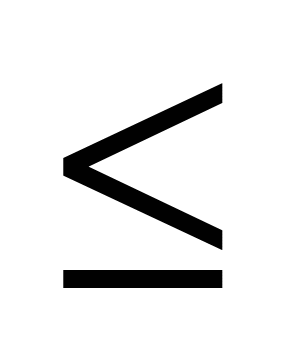 5), либо 5+х (если х5). Поэтому уравнение выглядит так: 2х=10 (при 3 5), либо 5+х (если х5). Поэтому уравнение выглядит так: 2х=10 (при 3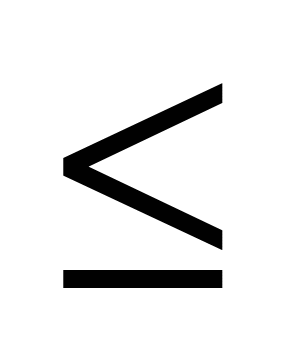 х х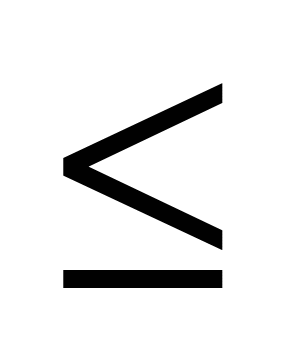 5) или х+3=10 (при х 5) или х+3=10 (при х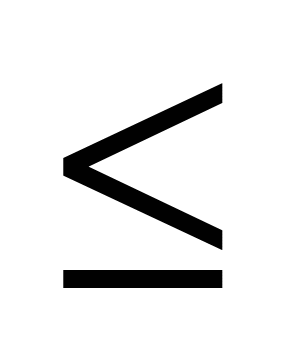 3) или 2х=5+х (при х5), откуда х=5 (при 3 3) или 2х=5+х (при х5), откуда х=5 (при 3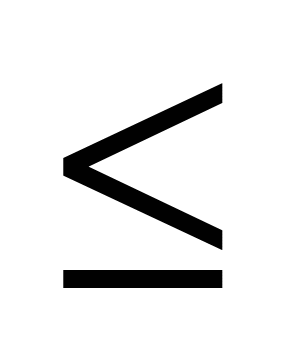 х х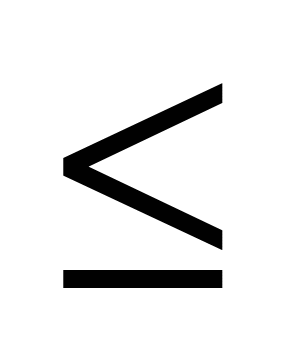 5) или х=7 (при х 5) или х=7 (при х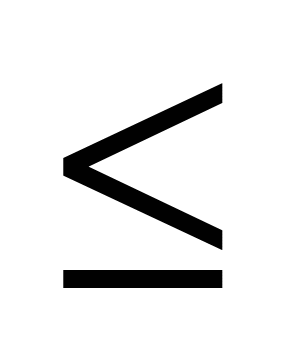 3) или х=5 (при х5). Следовательно, х=5. 3) или х=5 (при х5). Следовательно, х=5.
Ответ: х=5
1) Из первой кучки переложим 14 орехов во вторую кучку, при этом в кучках станет 8, 28 и 12 орехов. 2) Из второй кучки перекладываем в третью 12 орехов. В кучках стало 8, 16 и 24 ореха. 3) В первую кучку из третьей переложим 8 орехов. Получим по 16 орехов в каждой кучке.
Пусть х=423 133, тогда 423 134=х+1 и 846 267=2х+1. Заменим числа в выражении:  = =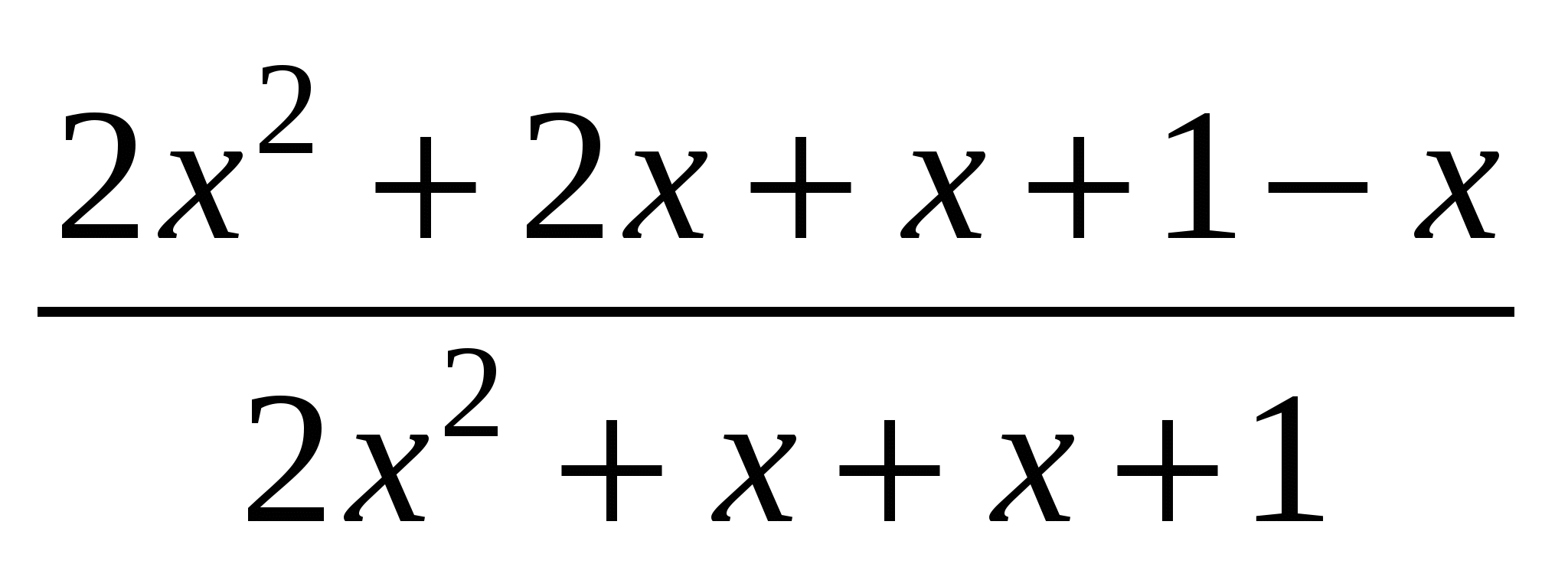 = =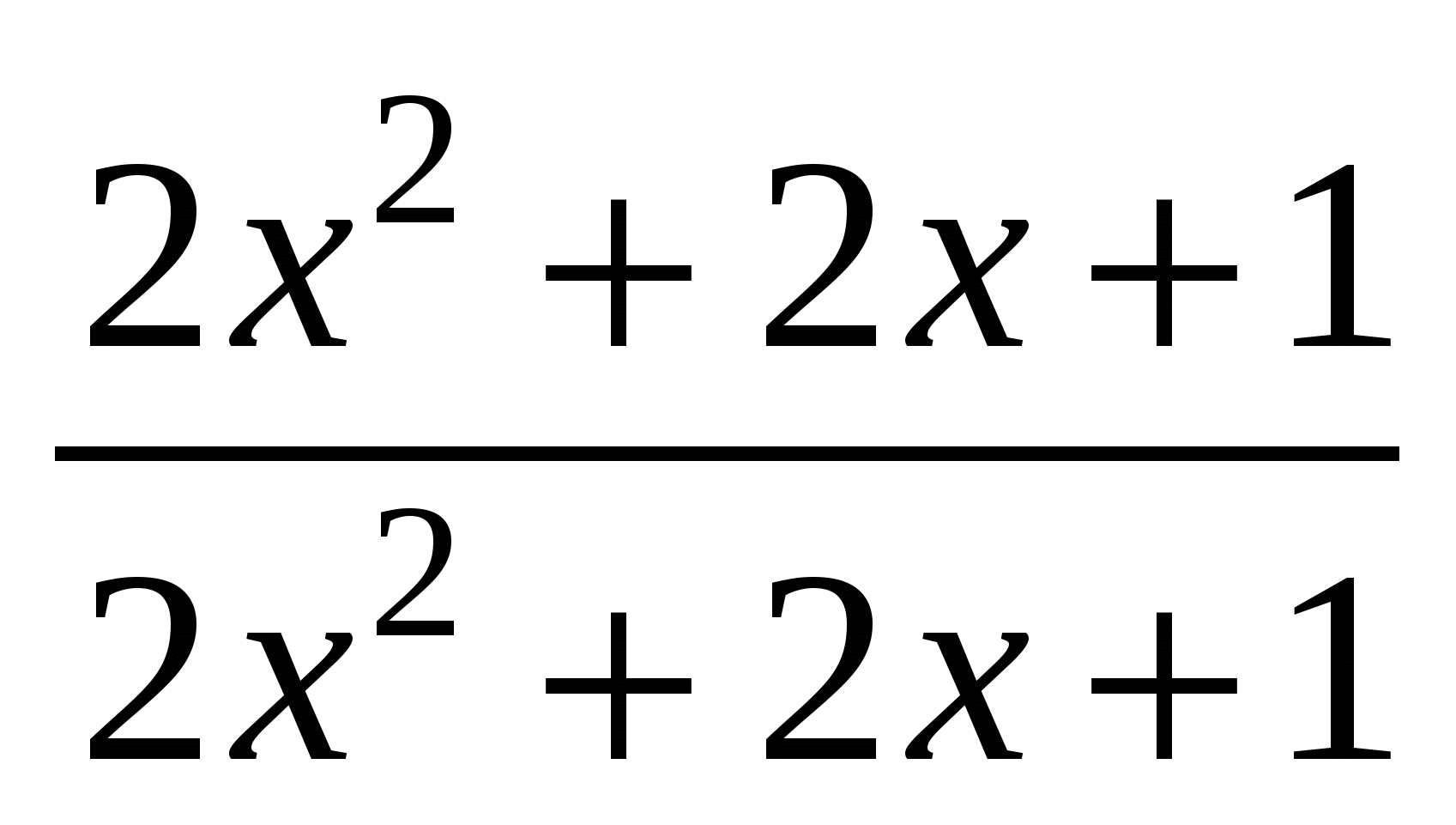 =1. =1.
Ответ: 1
Полторы курицы за полтора дня несут полтора яйца, значит одна курица несет одно яйцо за полтора дня. Курица, несущаяся быстрее в полтора раза, сносит одно яйцо в день. Следовательно, за полторы недели одна эта курица снесет десять с половиной яиц. В задаче спрашивается сколько кур нужно добавить к половинке курицы, значит нужно добавить еще полкурицы, чтобы за полторы недели мы получили 10 с половиной яиц.
Ответ: полкурицы
Ивану достаточно назвать числа x=100, y=10 и z=1, тогда Кощей назовет число, состоящее из тех цифр, которые он загадал (в том же самом порядке).
При раскрытии скобок, все слагаемые, содержащие х взаимно уничтожаются, поэтому получим уравнение 1=1, следовательно х – любое число.
Ответ: х – любое число
10.Возможны два случая: 1) одно из чисел a или b четное или оба четные, тогда Произ-
ведение, в котором хотя бы один из множителей число четное, является четным чис-
лом. 2) оба чесла нечетные, тогда их сумма – число четное и произведение опять будет
числом четным.
Пусть х (км/ч) скорость первого автомобиля, у (км/ч) скорость второго автомобиля.
Тогда х+у (км/ч) скорость их сближения. По условию машины встретились через 8 часов, следовательно, расстояние между городами А и В равно8(х+у) км. По условию задачи если бы были увеличены скорости, то 1,14х (км/ч) скорость первого автомобиля, а 1,15у (км/ч) скорость второго автомобиля, тогда (1,14х+1,15у) (км/ч) стала скорость сближения, а
7 (1,14х+1,15у) км расстояние между городами. Расстояние между городами мы выра-
зили дважды, приравняем:  . Откуда раскрыв скобки и перенеся . Откуда раскрыв скобки и перенеся
слагаемые, получим уравнение  , т.е. , т.е. 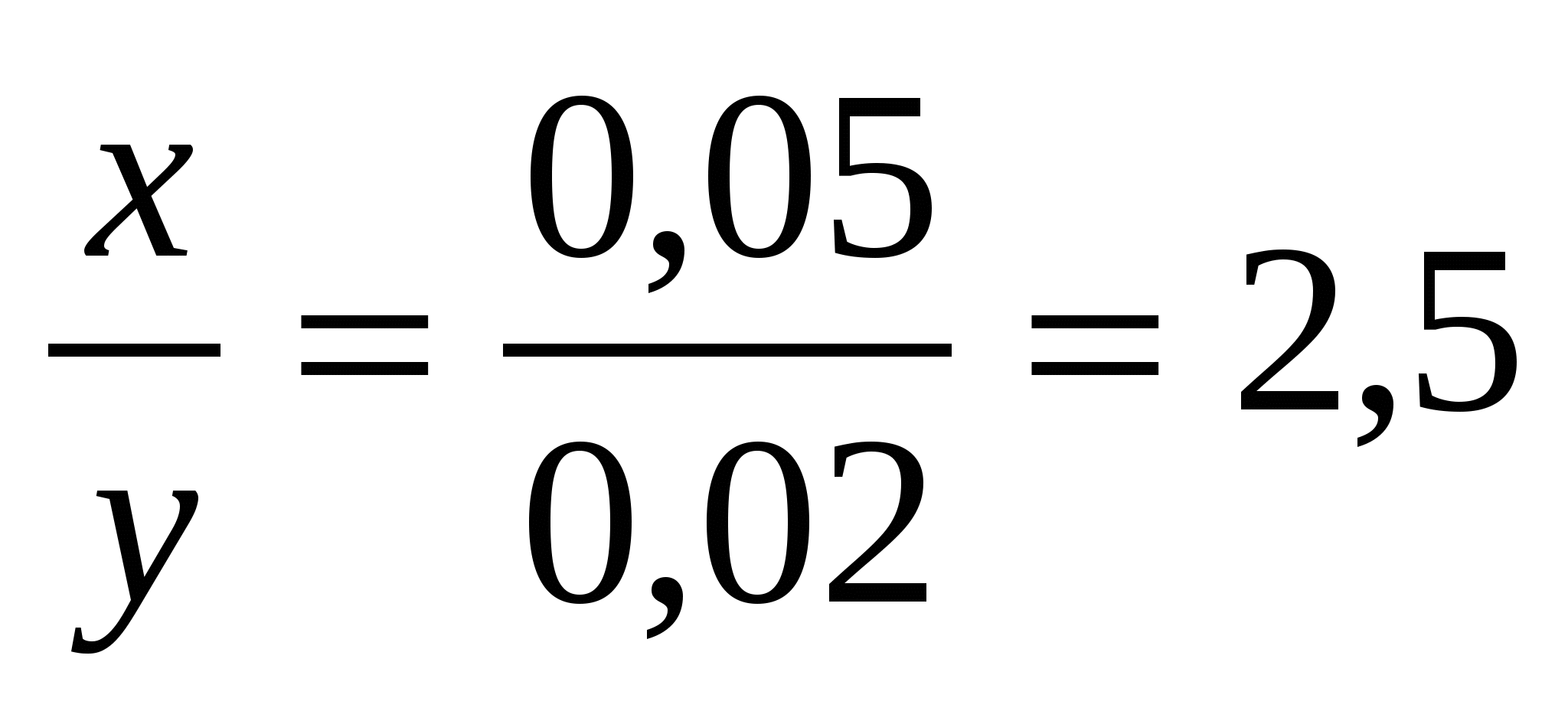 . Значит скорость первого . Значит скорость первого
автомобиля больше скорости второго автомобиля в 2,5 раза.
Ответ: скорость первого больше в 2,5 раза
Обозначим за 1 исходное количество нефти. Тогда 30%=0,3 – количество нефти, сливаемое в А, 1-0,3=0,7 – количество нефти, идущее по нефтепроводу в деревне В. В деревне В сливают 40% , т.е. 0,70,4=0,28, остальное 0,7-0,28=0,42 идет в деревню С. В этой деревне сливают половину нефти, что составляет 0,21 и столько же отправляется дальше. Таким образом, до конца нефтепровода доходит 0,21=21% первоначального количества нефти. Ответ: 21%

Решение: Можно, например так:
Первое взвешивание: первую и вторую гири сравниваем по весу с третьей.
Возможны следующие случаи: 1) 1+2=3, тогда 4 гиря фальшивая. Легче она или
тяжелее определим вторым взвешиванием: 1+3 сравним с 4, если 1+3>4, то 4 –
легче, если 1+3<4, то 4 тяжелее. 2) 1+2<3, тогда вторым взвешиванием сравним
1+3 и 4. При этом можем получить: а) 1+3>4, фальшивой будет 3 гиря, она
тяжелее, чем должна быть; б) 1+3<4, то фальшивая 1 гиря и легче; в) 1+3=4, то
2 гиря фальшивая и легче. 3) 1+2>3. Этом случае поступаем аналогично 2
случаю.
Ответ: можно
Пушкина мы ставим на первое место, а Маяковского и Пастернака «скрепим» и будем пока считать одной книгой. После Пушкина требуется поставить еще 3 книги. Это можно сделать 321=6 способами. Вернемся к «скрепленной» книге, состоящей из двух. Эти книги могут стоять так: сначала Маяковский, затем Пастернак и наоборот. Т.е. на самом деле, способов расставить все книги на полке будет в два раза больше, 62=12.
Ответ: 12 способов
8 класс.
Заметим, что два веника и один тазик вместе стоят ровно 4 рубля. Следовательно, Иван Иванович может купить на все имеющиеся у него деньги 10 веников и 5 тазиков.
Ответ: 10 веников и 5 тазиков
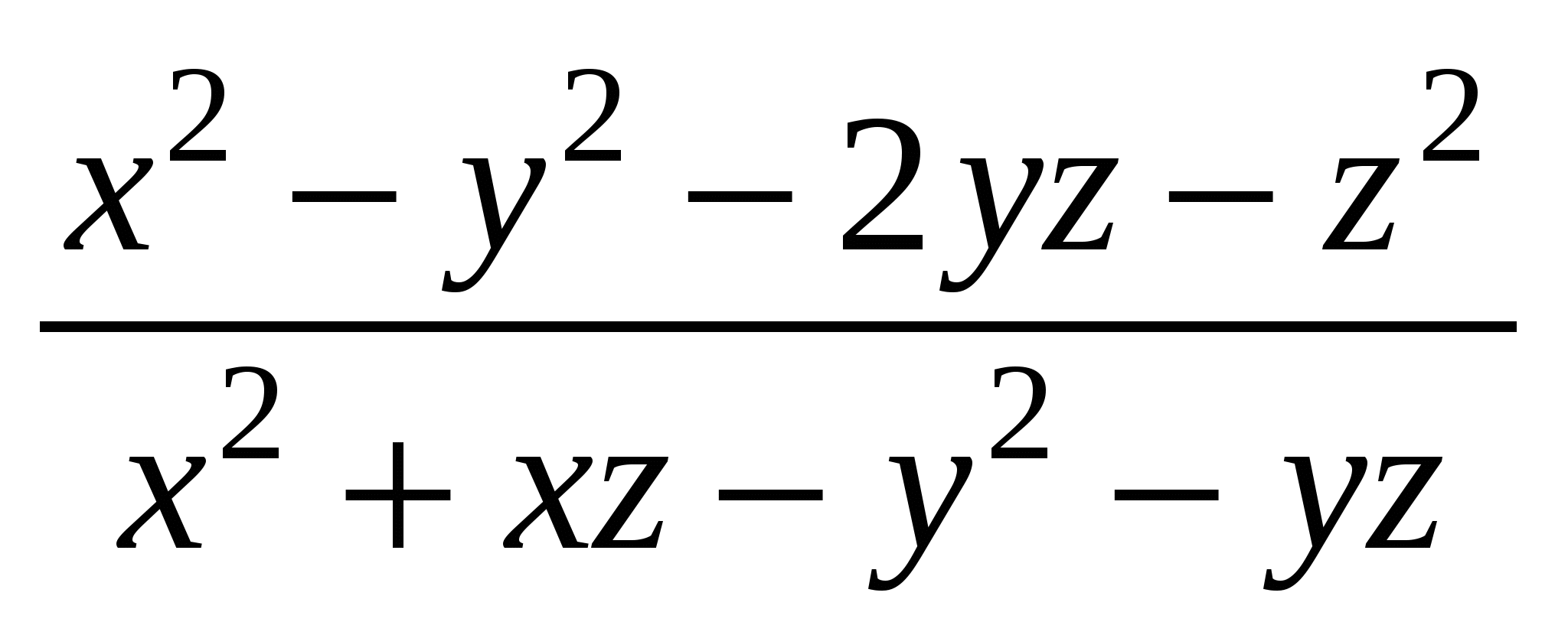 = =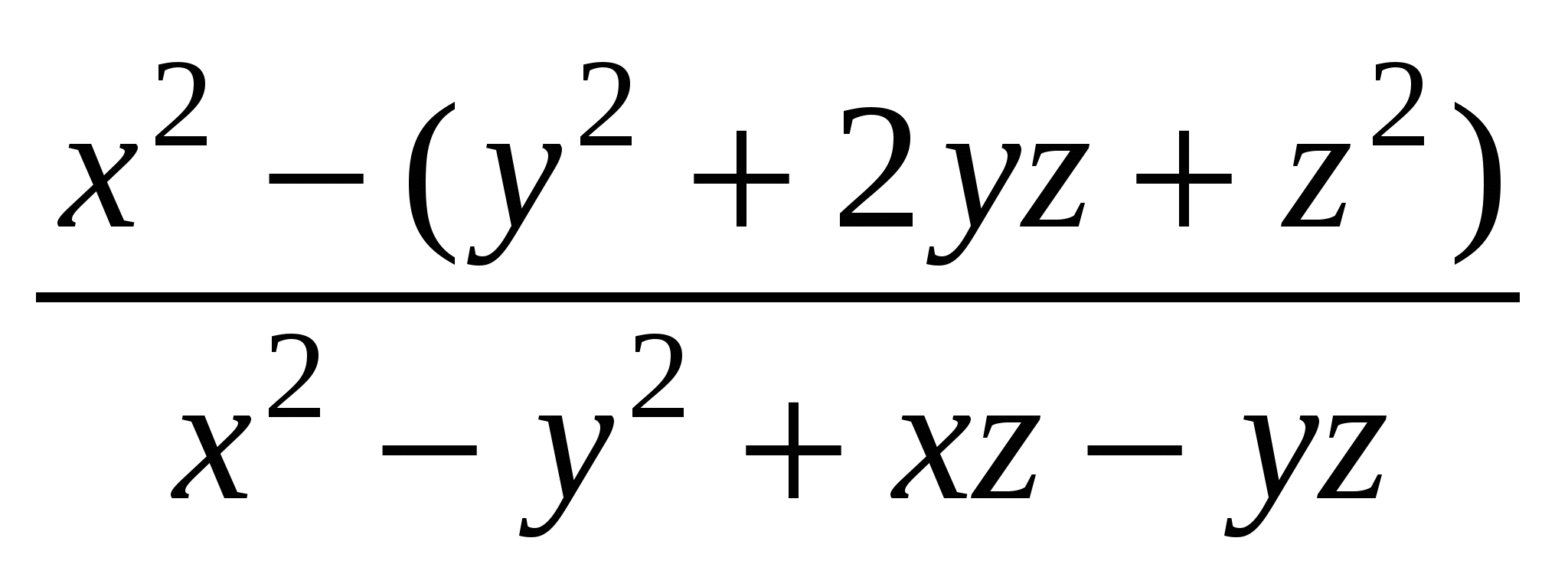 = =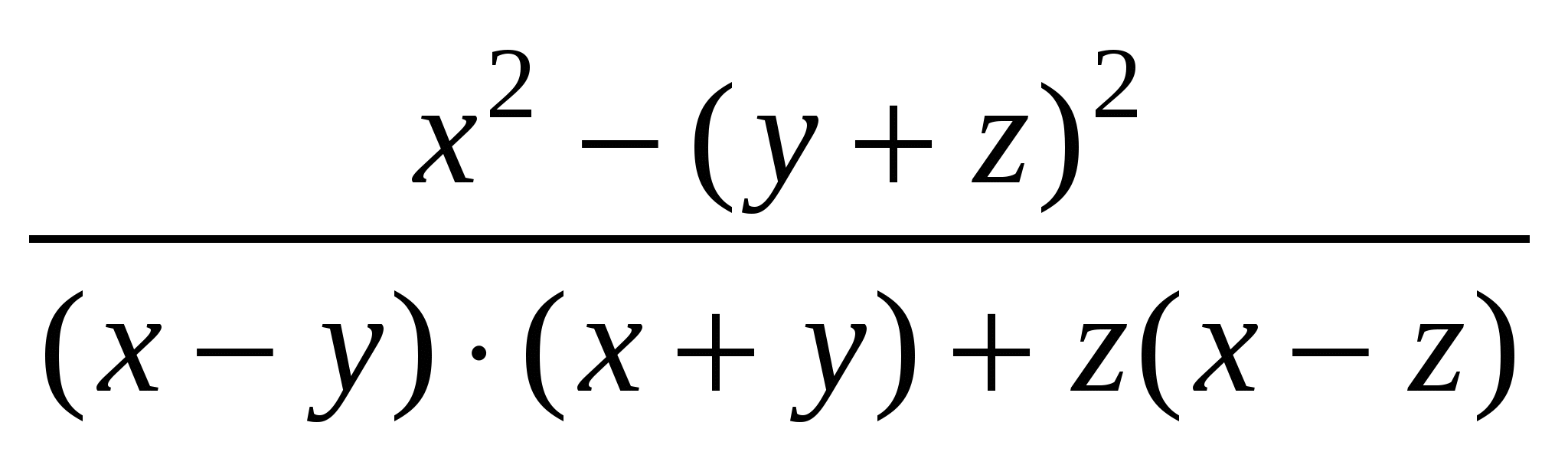 = =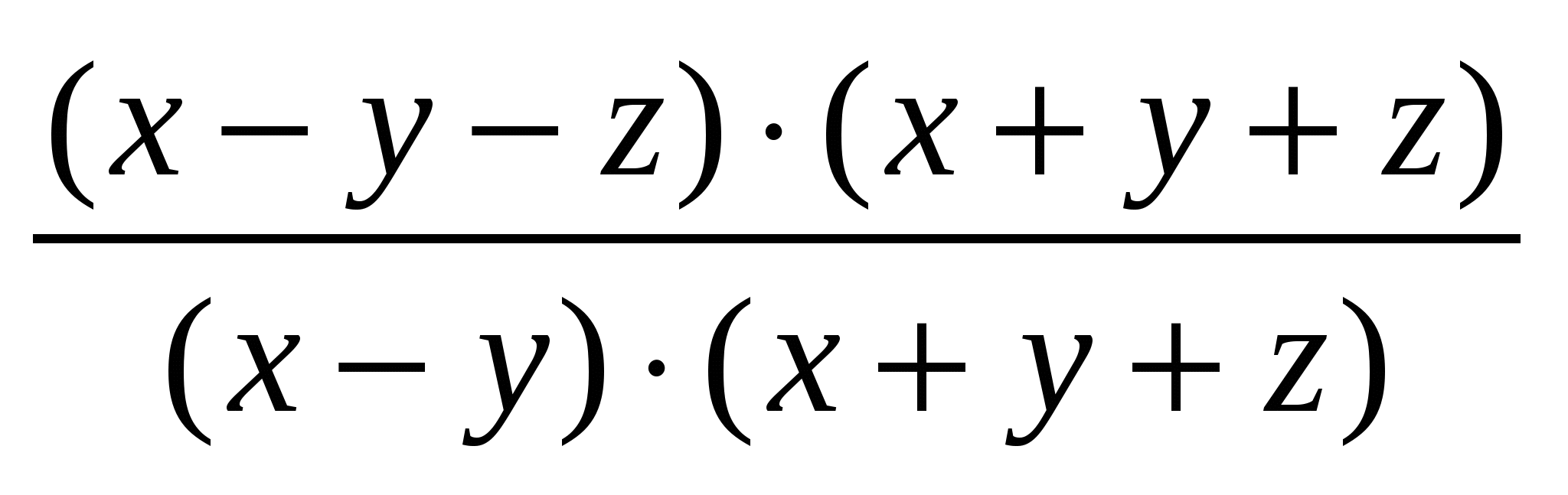 = =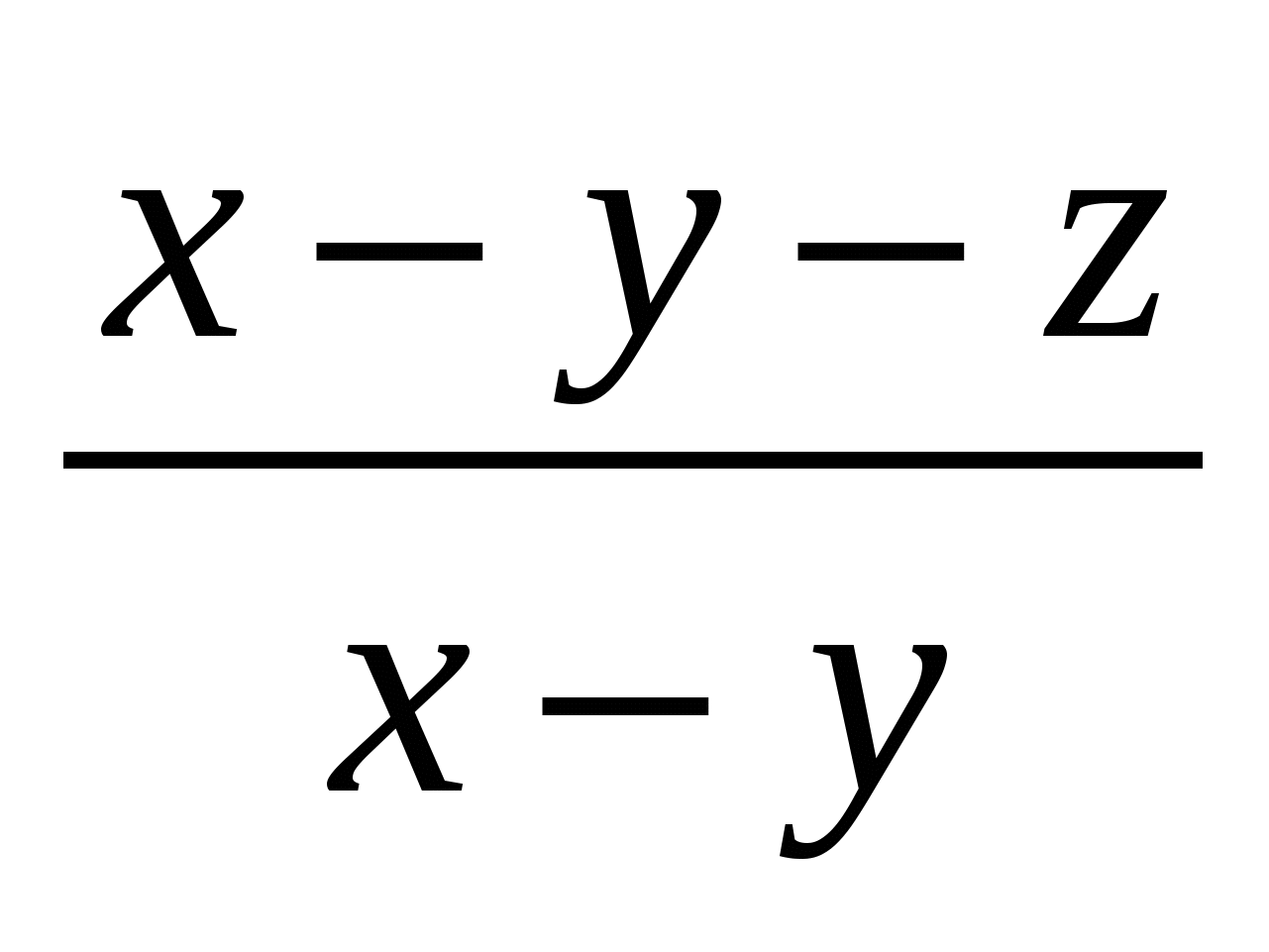 . .
Ответ: 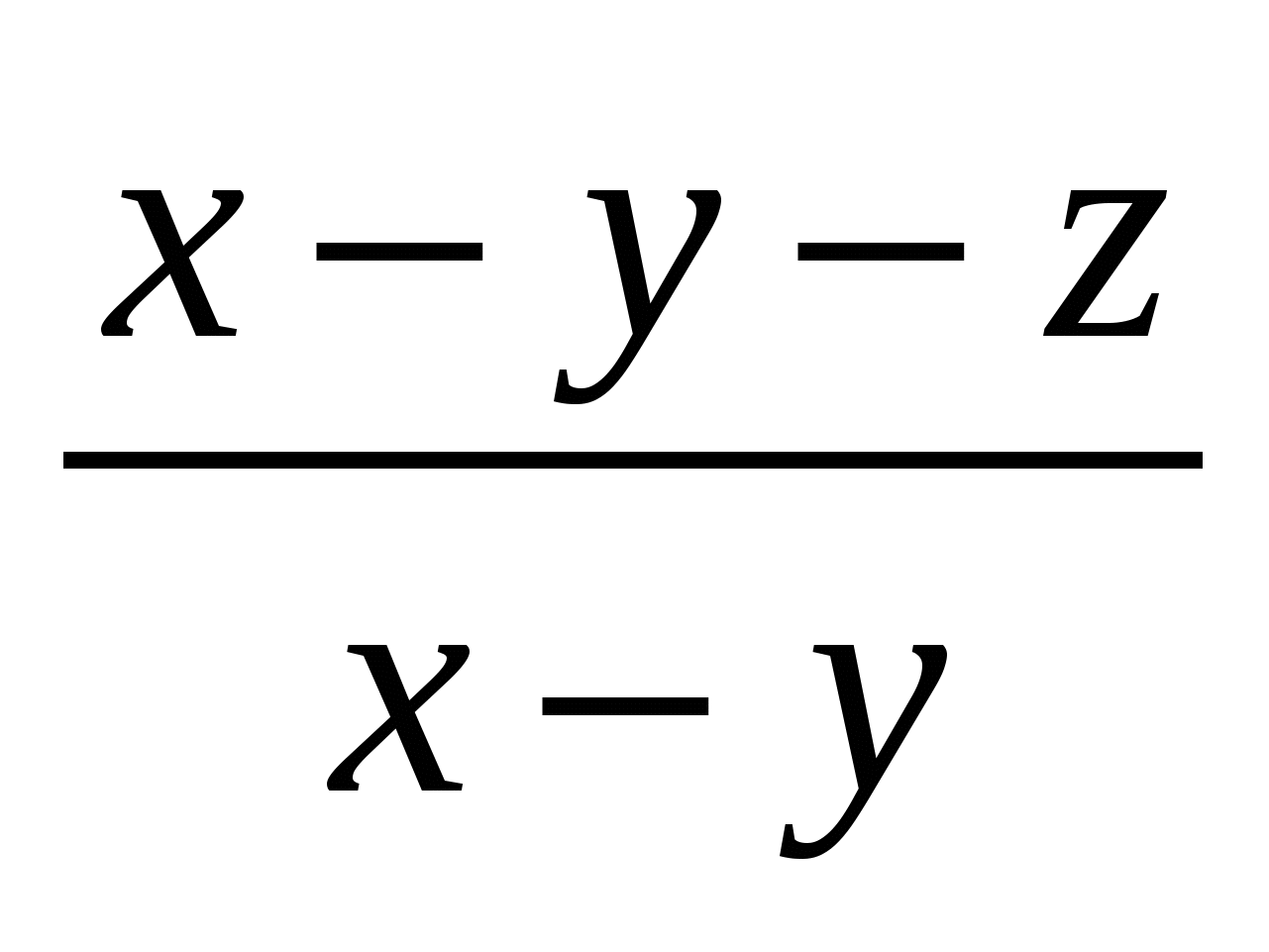
Пусть х (верст) проезжает первый путешественник в день, у (верст) проезжает второй путешественник в день, тогда (х+у) дней они были в пути. По условию второй за (х+у) дней проехал 525 верст, получаем первое уравнение у(х+у)=525. Первый за (х+у) дней проехал 525+175=700 верст, получаем второе уравнение х(х+у)=700. Имеем систему двух уравнений с двумя неизвестными:  . Решим эту систему. Разделив первое уравнение системы на второе, получим . Решим эту систему. Разделив первое уравнение системы на второе, получим 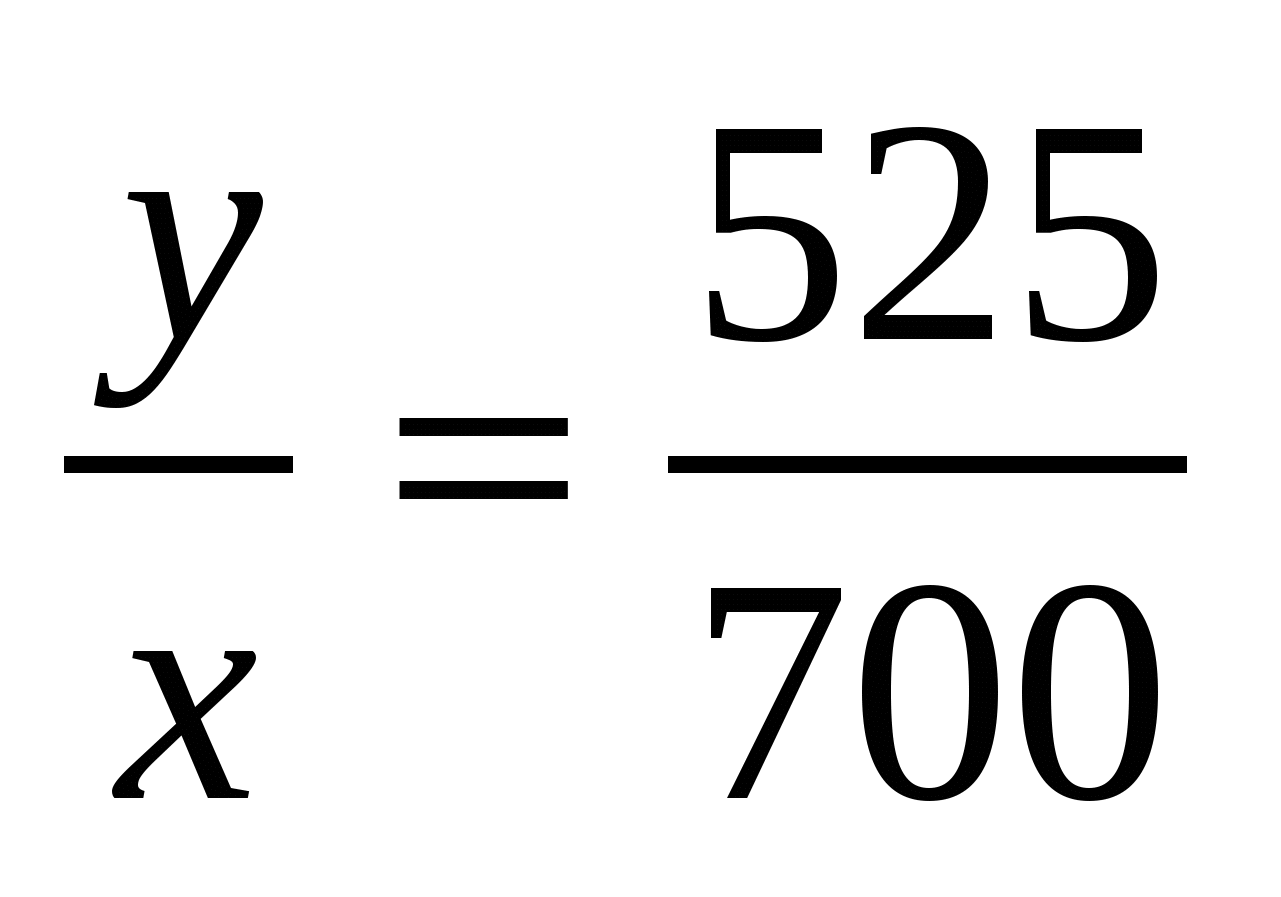 , откуда , откуда 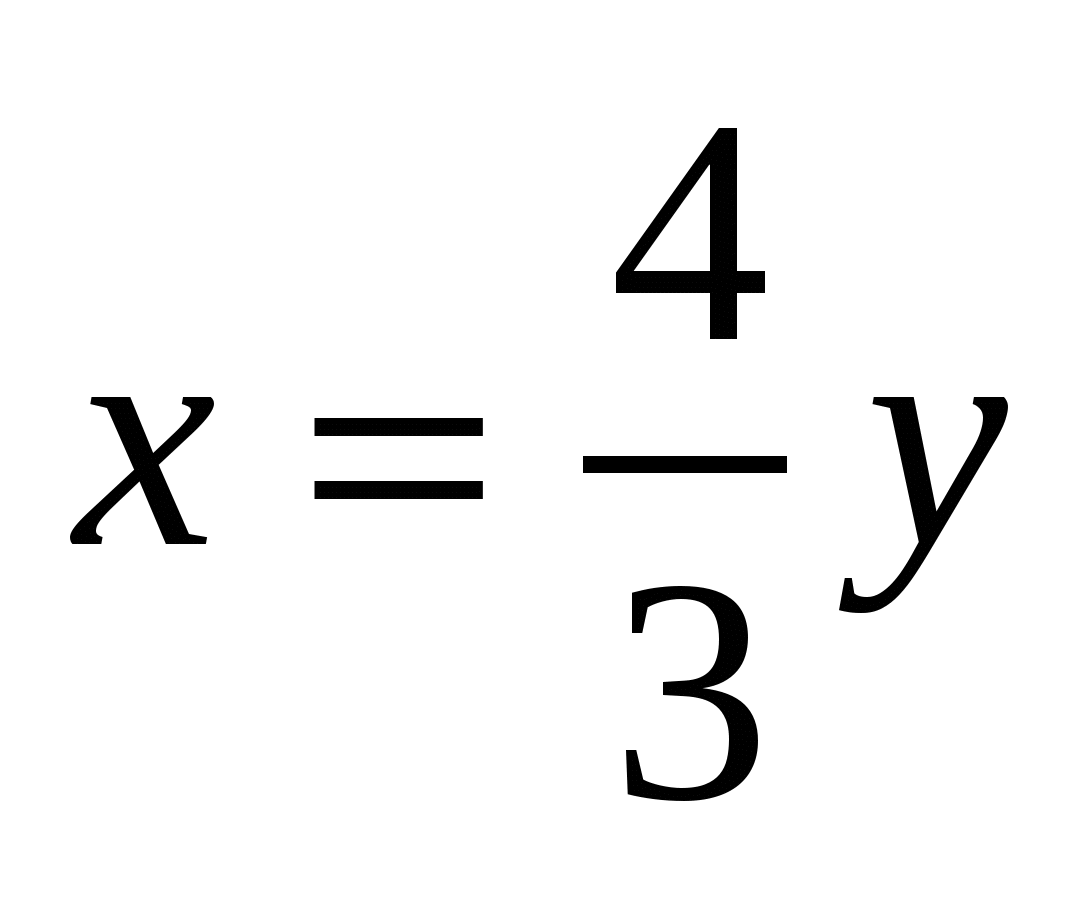 . Подставив во второе уравнение системы придем к уравнению . Подставив во второе уравнение системы придем к уравнению 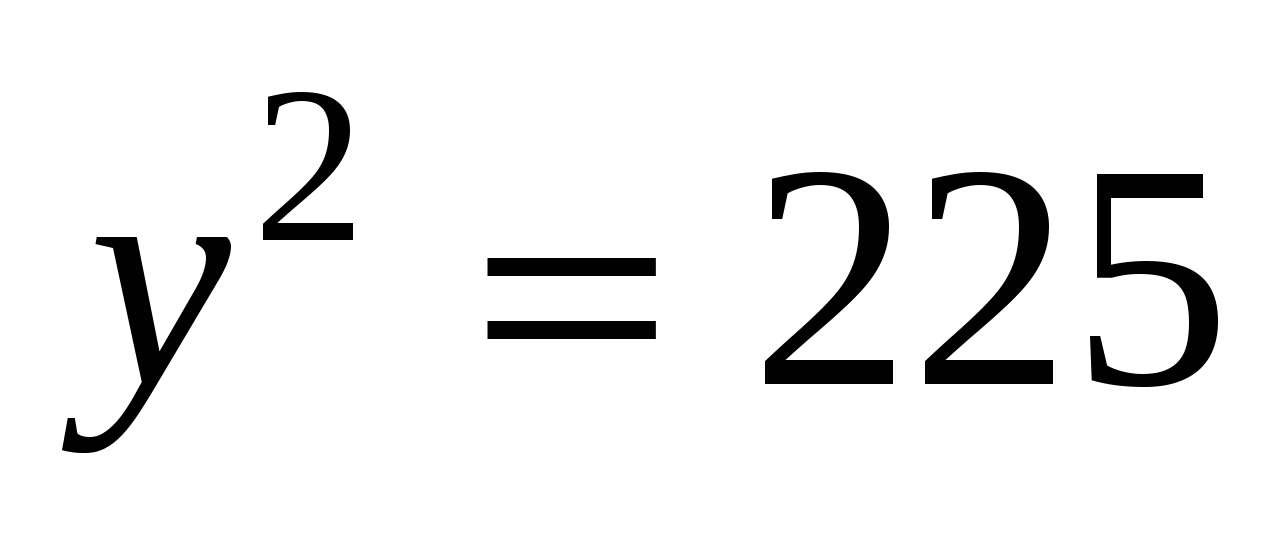 , отсюда у=15, а , отсюда у=15, а 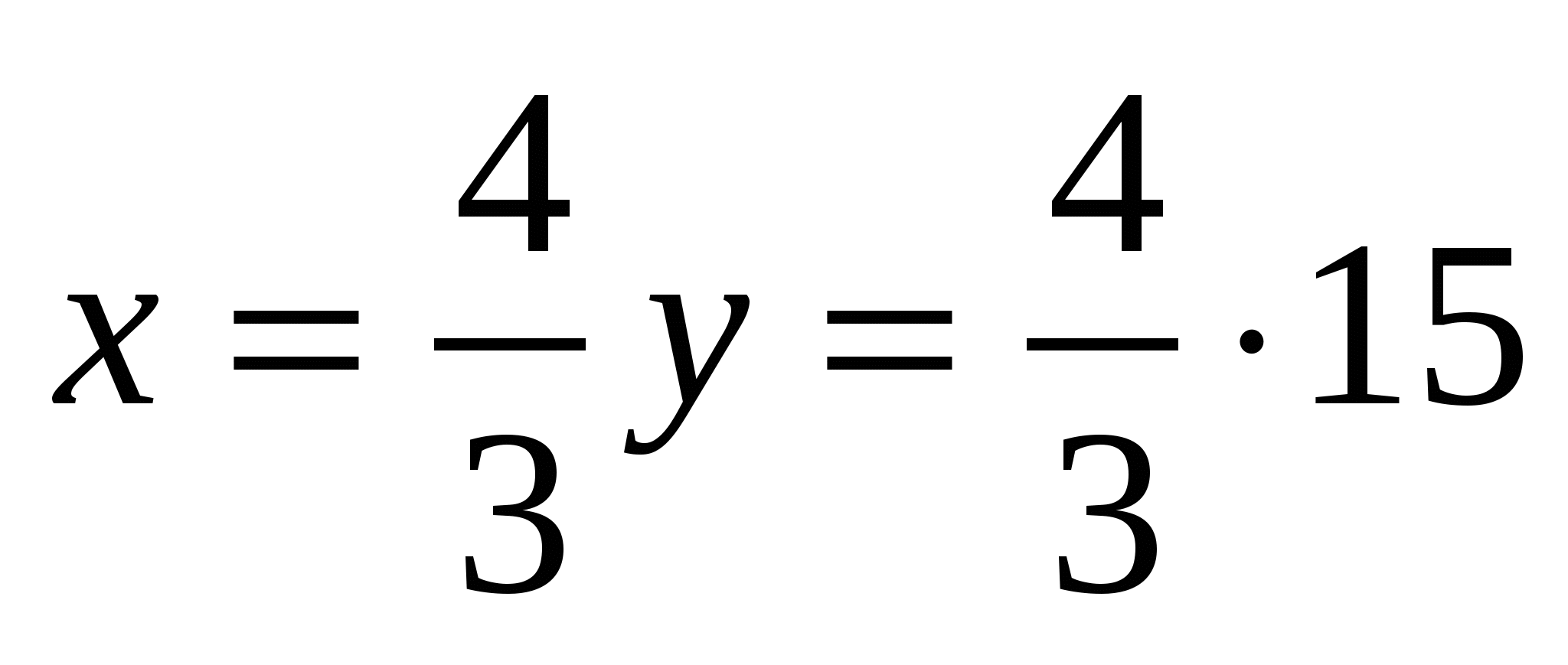 =20. Мы получили, что первый проезжает 20 верст в день, а второй – 15 верст в день. =20. Мы получили, что первый проезжает 20 верст в день, а второй – 15 верст в день.
Ответ: 20 и 15 верст
Пусть х – числитель обыкновенной дроби, а у – ее знаменатель, т.е. на доске была записана дробь 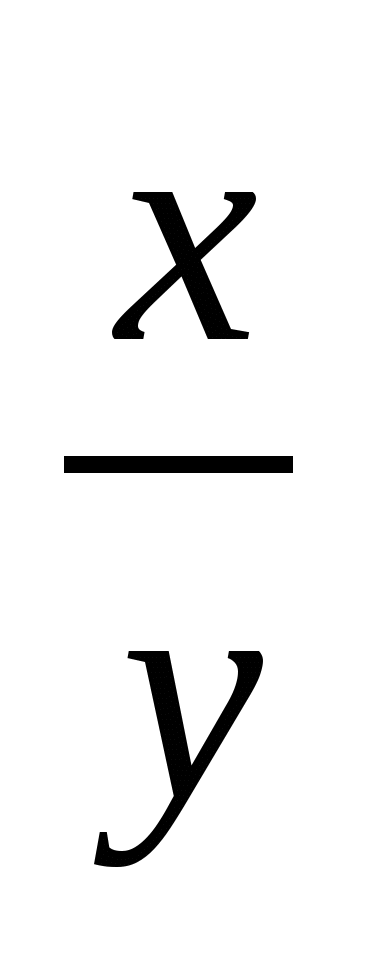 . Затем к знаменателю дроби прибавили числитель, получили новую дробь . Затем к знаменателю дроби прибавили числитель, получили новую дробь 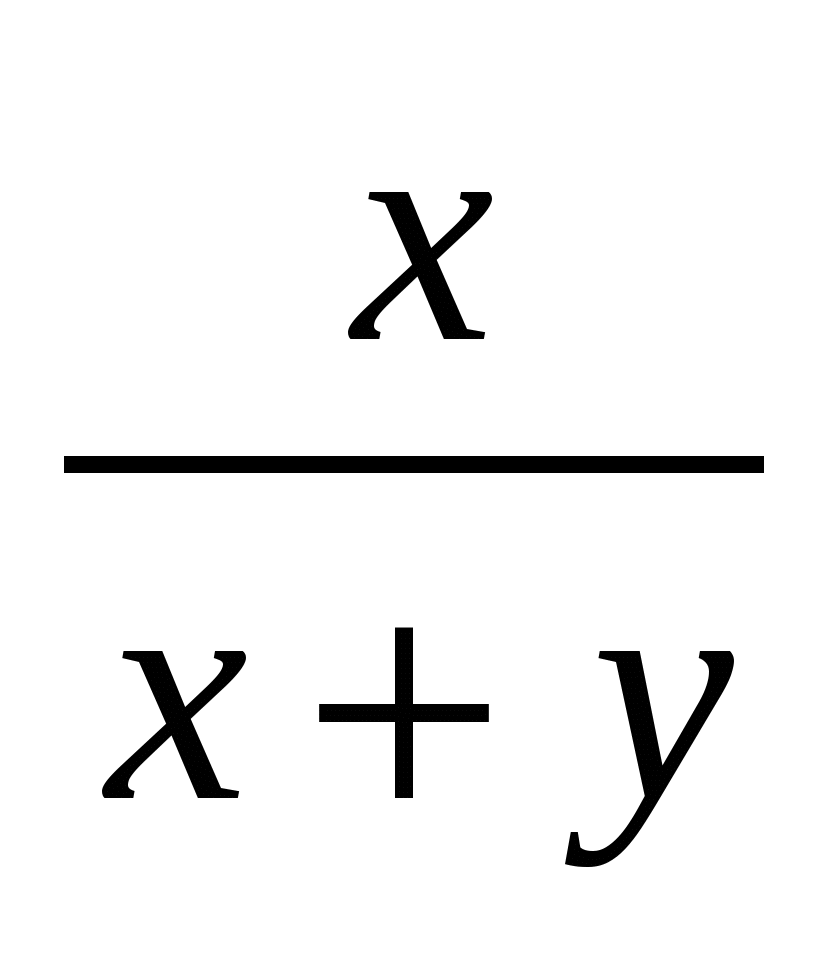 . К числителю новой дроби прибавили ее знаменатель, получив . К числителю новой дроби прибавили ее знаменатель, получив 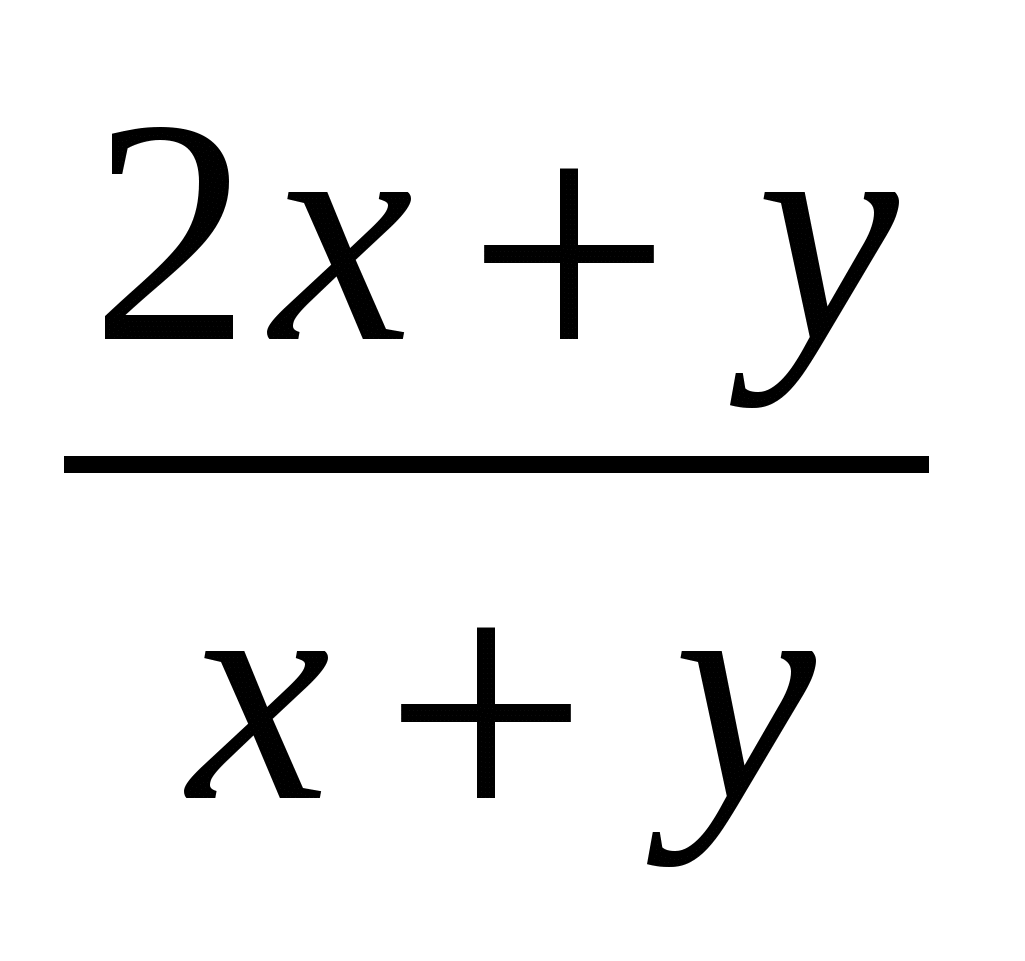 . После этого, к знаменателю полученной дроби прибавили числитель, мы получили следующую дробь . После этого, к знаменателю полученной дроби прибавили числитель, мы получили следующую дробь 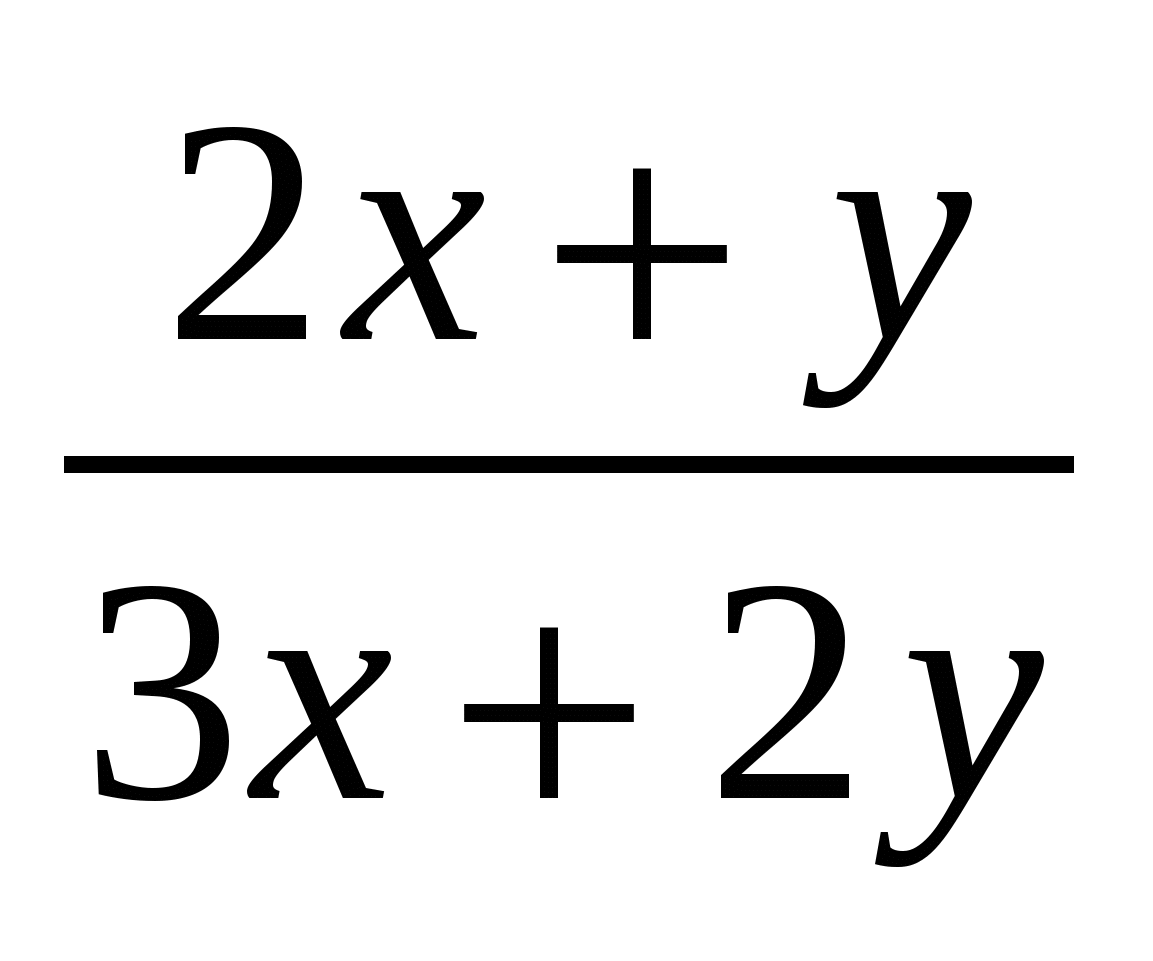 . Оказалось, что эта дробь равна . Оказалось, что эта дробь равна 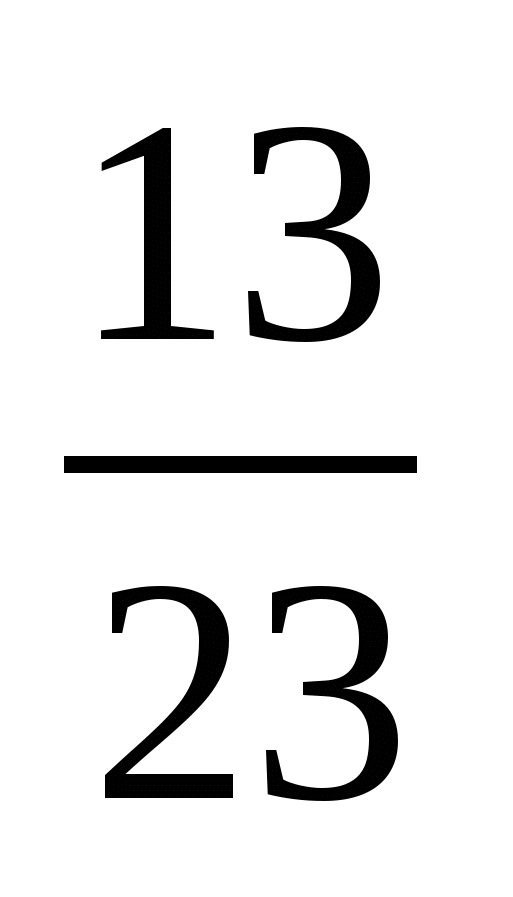 . Перейдем к системе уравнений: . Перейдем к системе уравнений:  . Из этой системы находим, что х=3, у=7. Значит, исходная дробь была равна . Из этой системы находим, что х=3, у=7. Значит, исходная дробь была равна  . .
Ответ: 
Заметим, что при прибавлении к любым двум числам по единице, сумма всех данных чисел не изменит своей четности. Она будет той же четности, что и 1+2+3+4+5+6=21, т.е. нечетной. Что получилось, если бы мы смогли уравнять все числа? В этом случае мы бы получили сумму шести одинаковых чисел, и она делилась бы на 6, т.е. была четной. Но разрешенными действиями с данными числами мы не можем получить четную сумму чисел, следовательно, уравнять их не сможем.
Ответ: нельзя
Суть игры в том, чтобы уравнивать число шариков в ящиках. Это можно сделать первым ходом, взяв из второго ящика 30 шариков. Партнер обязательно нарушит полученное равенство, а мы опять его восстановим. Число шариков все время убывает, и когда-нибудь игрок, уравнивающий число шариков, доведет это равенство до 0 : 0, т.е. выиграет.
Ответ: нужно начать игру, взяв из второго ящика 30 шариков, и в дальнейшем
каждый раз уравнивать их число
Общее расстояние, которое они прошли к моменту первой встречи, равно ширине реки. Когда они встречаются во второй раз, суммарное расстояние равно утроенной ширине реки, что потребовало в 3 раза больше времени. К моменту первой встречи один из паромов прошел 720 м, тогда к моменту второй встречи 7203=2160 м. Но это расстояние на 400 м превышает ширину реки. Следовательно, ширина реки 1760 м.
Ответ: 1760 м
Из чисел a, b, c по крайней мере два одинаковой четности (т.е. четные или нечетные). Тогда 3a, 3b, 3c имеют ту же четность, что и a, b, c. Следовательно, хотя бы одна из скобок 3a-b, 3b-c, 3c-a будет четна, и вся левая часть равенства также должна быть числом четным, а справа нечетное число 5005.
Ответ: не существует таких чисел
Из третьего условия 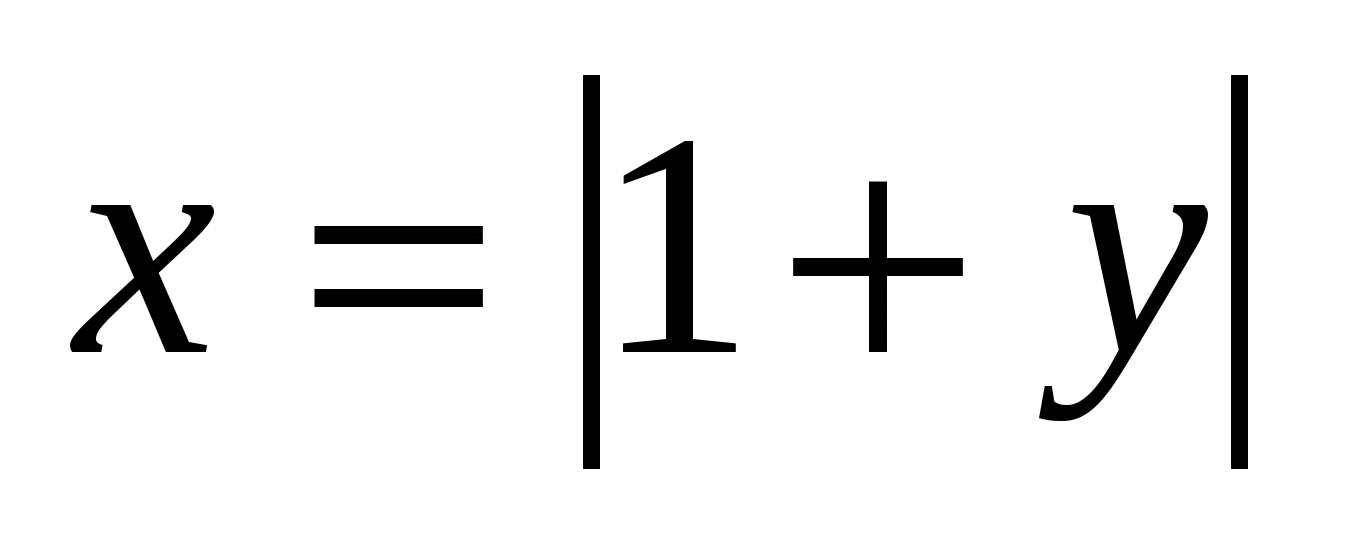 , т.е. х 0 и одновременно , т.е. х 0 и одновременно 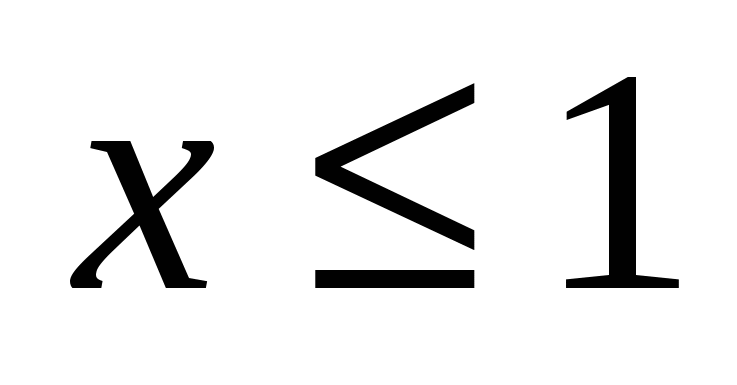 , следовательно, , следовательно,  . Тогда первое и третье условия выполняются вместе: в . Тогда первое и третье условия выполняются вместе: в 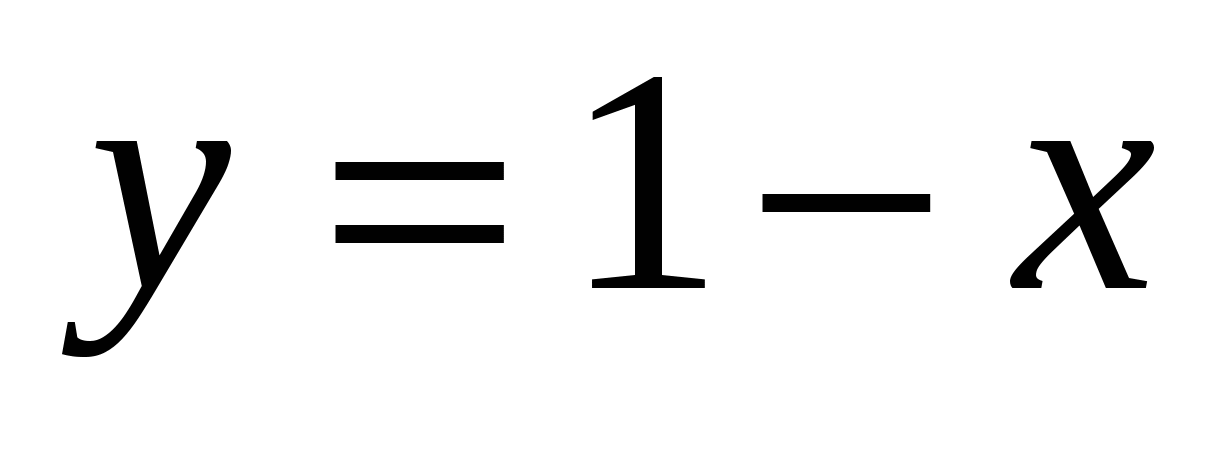 подставим подставим 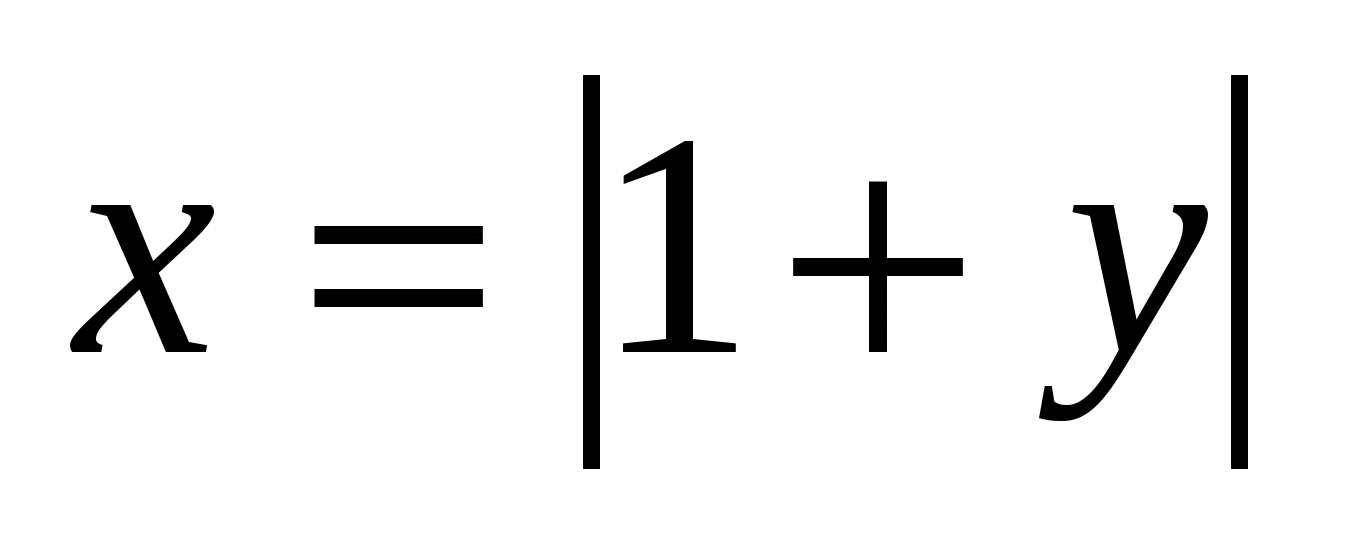 , получаем уравнение , получаем уравнение 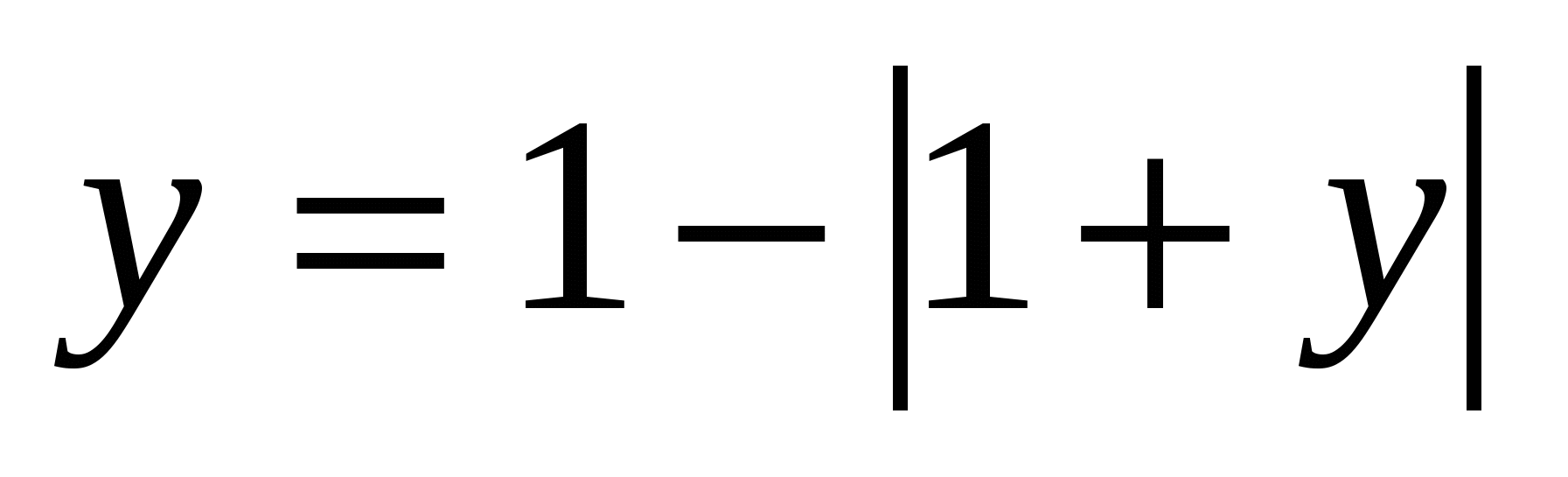 . Решением этого уравнения является у=0, тогда х=1. . Решением этого уравнения является у=0, тогда х=1.
Ответ: х=1, у=0
Общий вес бочек 1+2+3+…+19+20=210 пудов, т.о., в каждую машину нужно положить по 70 пудов. Это можно сделать, например так: первая машина – бочки весом 1, 2, 10, 18, 19 и 20 пудов; вторая машина – бочки весом 3, 4, 5, 11, 14, 16 и 17 пудов; третья машина – бочки весом 6, 7, 8, 9, 12, 13 и 15 пудов.
Общий все бочек во втором случае равен 1+2+3+…+9+10=55 пудов. Т.к. 55 не
делится на 3 , то поровну эти бочки мы разложить в три грузовика не сможем.
Пусть в корзине х яблок, у груш. Если добавить туда столько же яблок, сколько сейчас там груш (в штуках), то яблок станет х+у. Тогда процент яблок будет  = =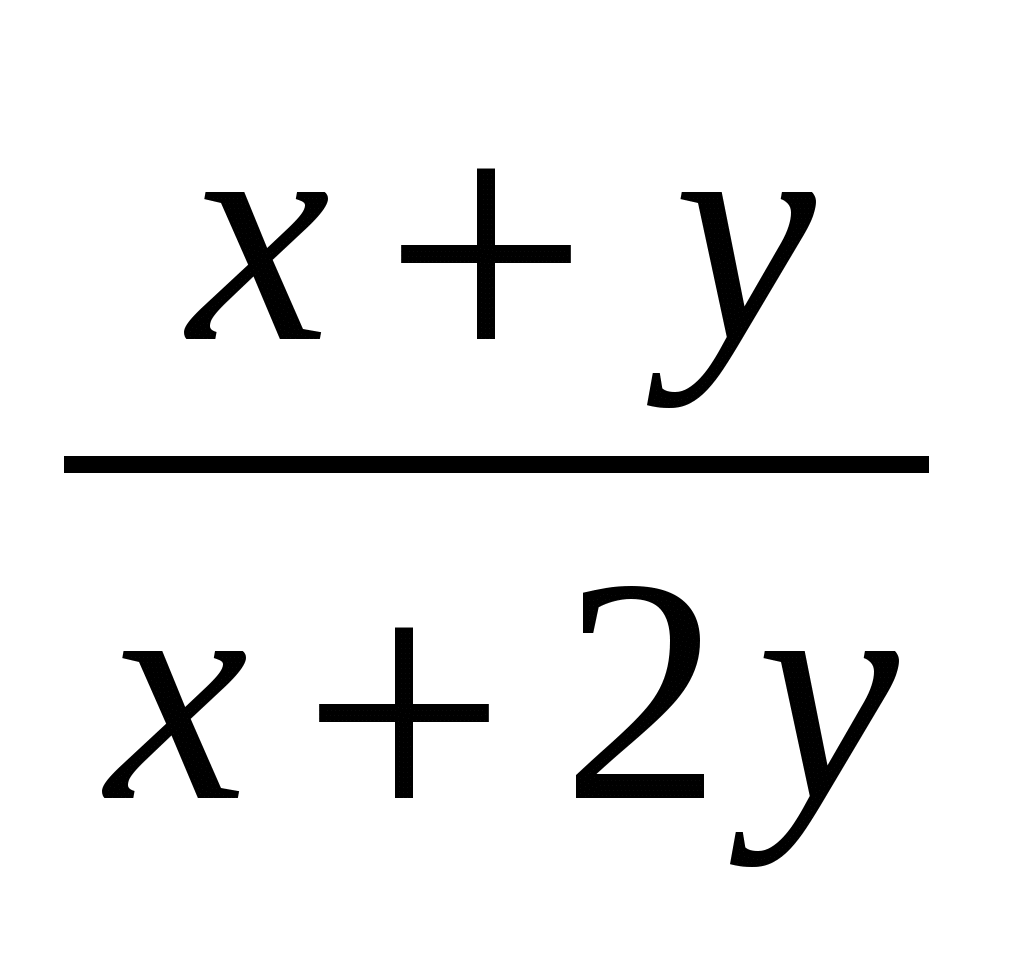 . Если же добавить в корзину столько груш, сколько сейчас там яблок, то груш станет х+у. Тогда процент яблок в этом случае равен . Если же добавить в корзину столько груш, сколько сейчас там яблок, то груш станет х+у. Тогда процент яблок в этом случае равен 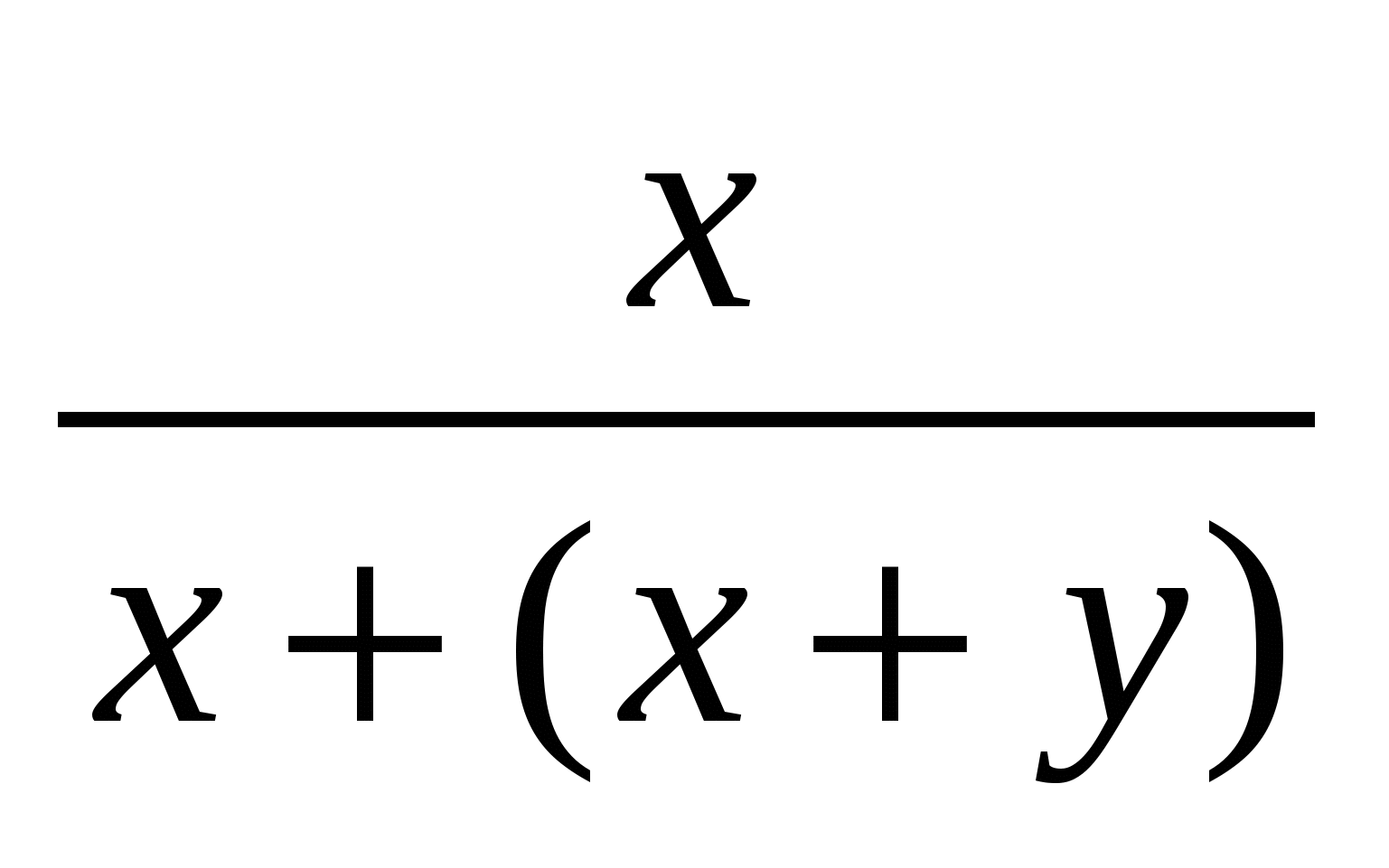 = =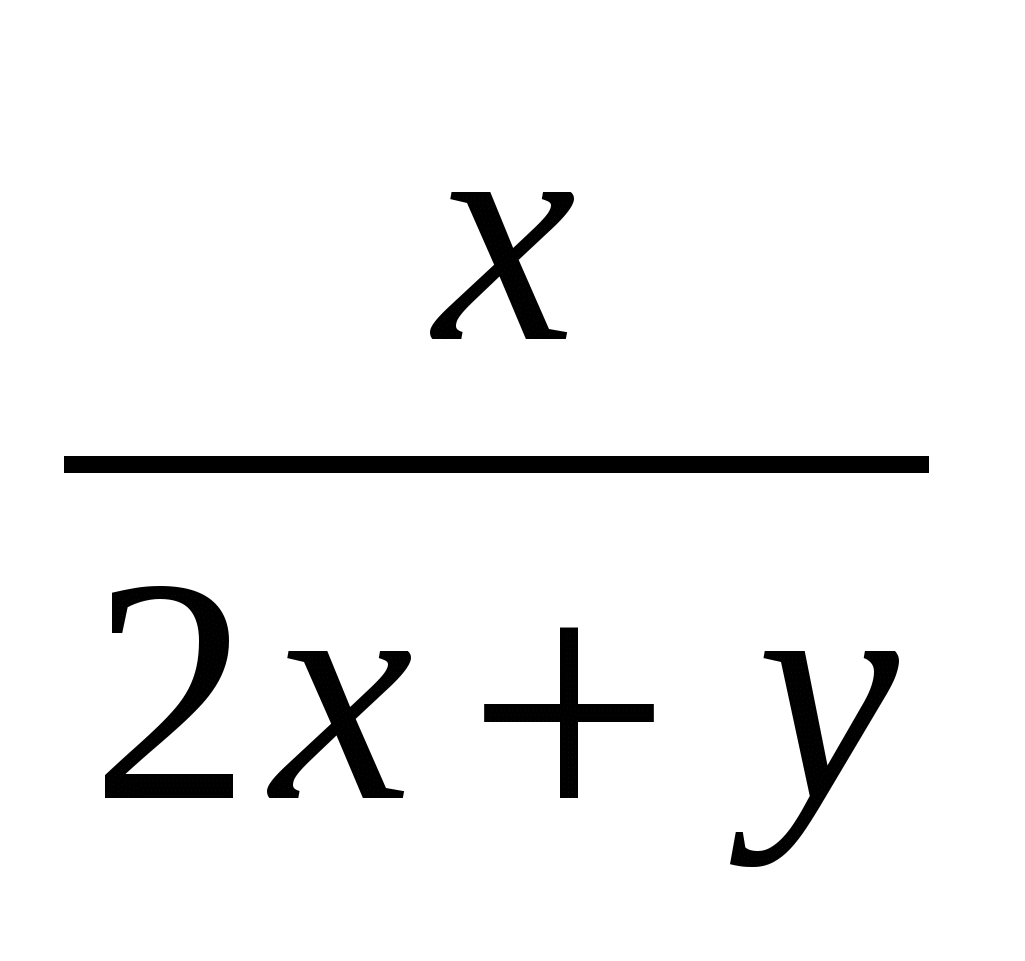 . По условию, процент яблок в первый раз в 2 раза больше, чем во второй раз, получаем уравнение: . По условию, процент яблок в первый раз в 2 раза больше, чем во второй раз, получаем уравнение: 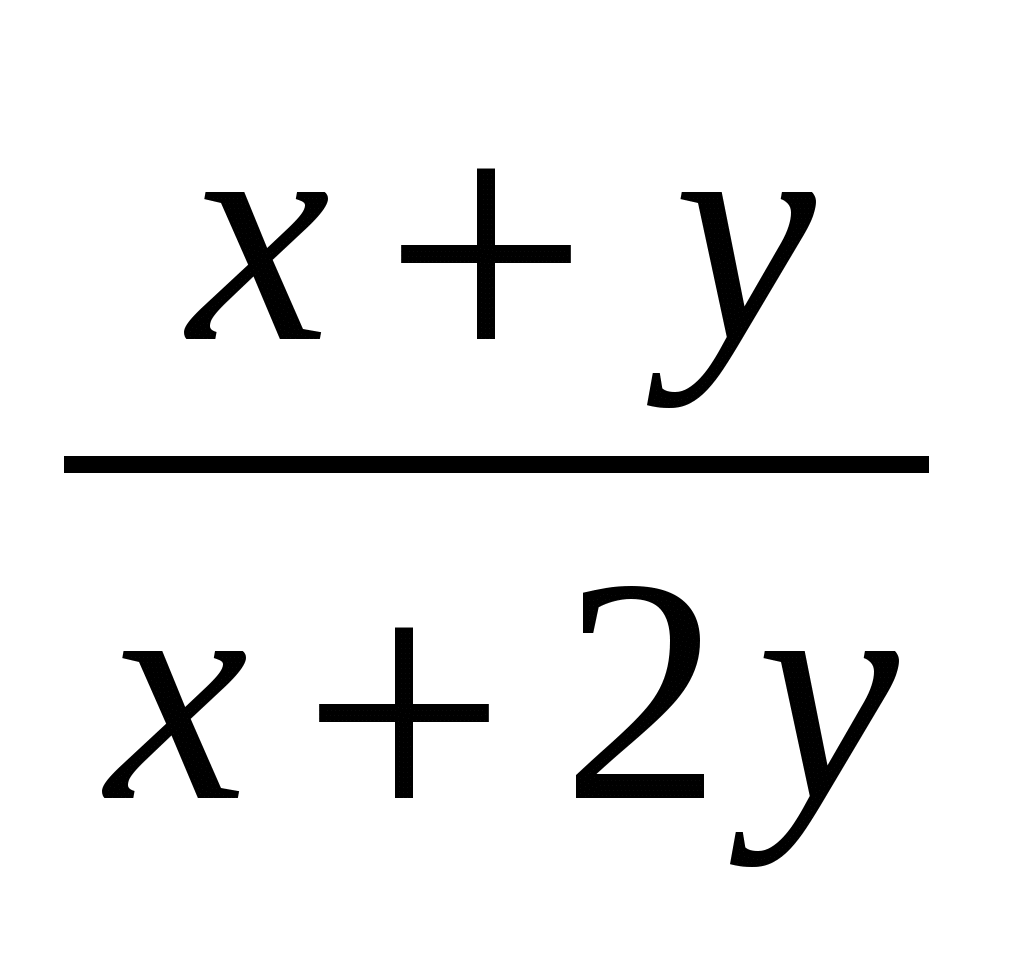 = = . Путем преобразований получаем уравнение . Путем преобразований получаем уравнение 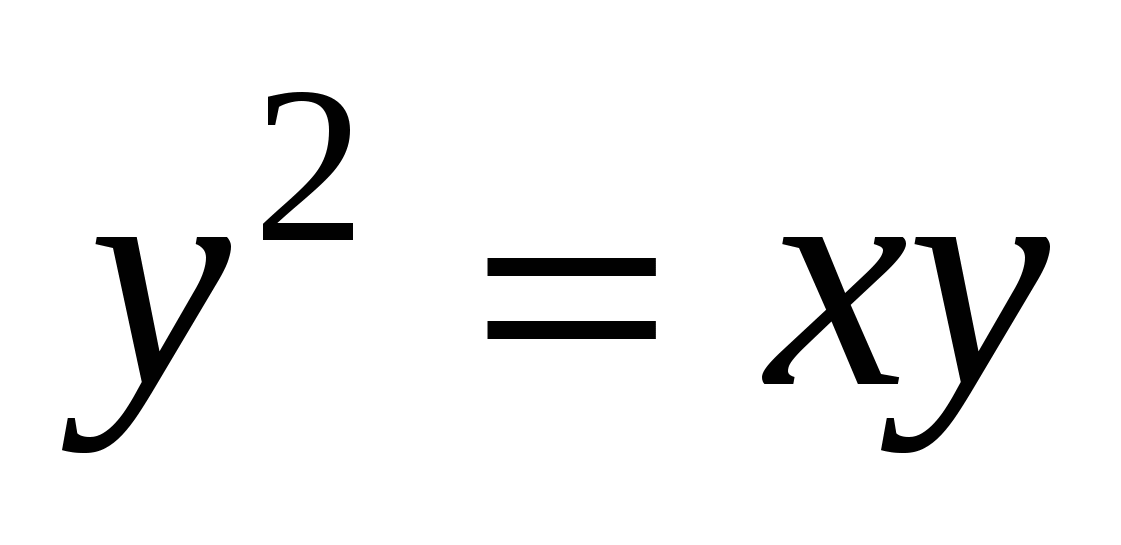 . Отсюда у=0 (не подходит по смыслу) или у=х. Значит, первоначально яблок и груш было поровну. Следовательно, яблок в корзине 50%. . Отсюда у=0 (не подходит по смыслу) или у=х. Значит, первоначально яблок и груш было поровну. Следовательно, яблок в корзине 50%.
Ответ: 50%
2004=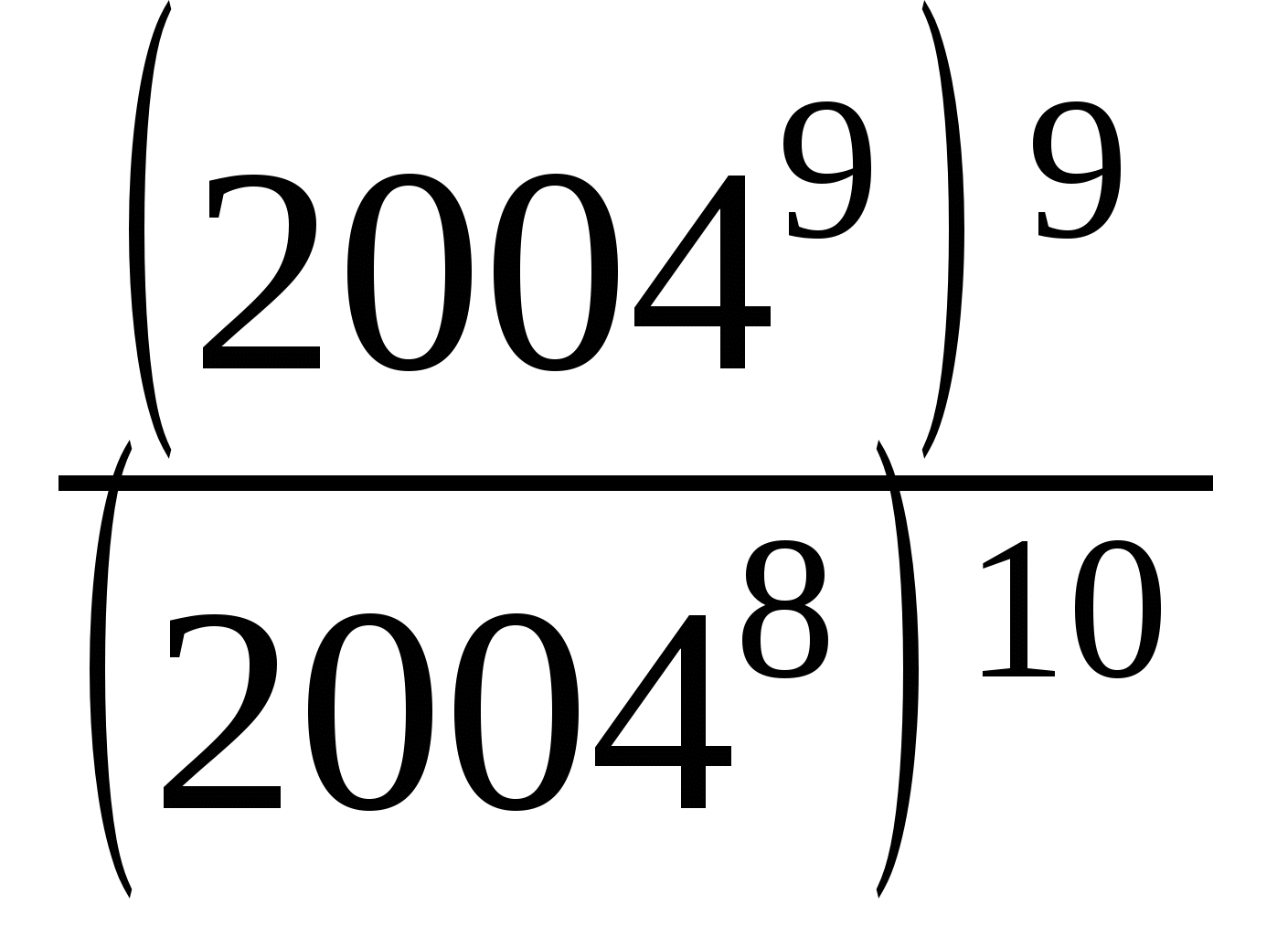
13. Это можно сделать например так:
-
14.Участок парка, где может гулять собачка, выделен на рисунке серым цветом.
15. Ладья с поля а1 должна попасть на поле h6, двигаясь только вправо и вверх по
одной клетке. Заполним клетки шахматной доски числами, которые показывают,
сколькими способами ладья может на них попасть. Начиная заполнять клетки с
ячейки с номером а1, замечаем, что число способов, которыми ладья может
попасть например в с3, получается сложением способов, которыми она попадает
в b3 и с2. Легко заполнив таблицу, получаем, что в h6 ладья попадет 729
способами. Заметим, что некоторые клетки шахматной доски остались пустыми,
т.к. ладья двигается только вправо и вверх.
8
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
6
|
1
|
6
|
21
|
56
|
126
|
252
|
462
|
792
|
5
|
1
|
5
|
15
|
35
|
70
|
126
|
210
|
330
|
4
|
1
|
4
|
10
|
20
|
35
|
56
|
84
|
120
|
3
|
1
|
3
|
6
|
10
|
15
|
21
|
28
|
36
|
2
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
h
|
Ответ: 729 способов
9 класс.
Да, можно. Одновременно поджигаем один из шнуров за два конца, а второй – за один. Когда первый шнур прогорит полностью, продёт полминуты. Затем соединяем концы второго шнура (от которого осталась не обязательно половина по длине, но половина по времени горения). Пока прогорит второй шнур, продёт ещё 15 секунд.
Нет, не может. Предположим противное: пусть мы нашли такие числа. Ни одно из чисел не равно 0 (0, умноженный на следующее по часовой стрелке, не может быть больше 0). Значит, числа положительные или отрицательные. Числа не могут быть разных знаков, потому что если за отмеченным положительным числом по часовой стрелке идёт отрицательное, то их произведение меньше отмеченного числа. Все числа не могут быть отрицательными, так как их сумма положительна. Значит, все числа по- ложительны. Если хотя бы одно из чисел не больше 1, отметим число, стоящее от него против часовой стрелки. Тогда произведение будет меньше отмеченного числа. Значит, все числа больше 1. Но тогда сумма чисел больше 2. Противоречие.
В каждом прямоугольнике 4 х 8 находится четыре ладьи (так как такой прямоугольник состоит из 4 строк или 4 столбцов). Разобьем доску на 4 квадрата 4 х 4. Пусть x ладей стоит в левом верхнем квадрате, тогда 4-x ладей в левом нижнем и 4-(4-x) ладей в правом нижнем. Но 4-(4-x)=x.
Разобьем доску на три области как показано на рисунке. Сумма чисел в каждой равна 2 (так как все клетки области, в том числе закрашенные, являются соседями или первой закрашенной клетки, и сумма чисел в них 1, или второй закрашенной клетки, и сумма чисел в них тоже 1). Таким образом, ответом в задаче может быть только 6.
Следующий пример показывает, что сумму 6 получить можно. Для этого в закра-
шенные клетки запишем числа 1, в остальные 0. Пример не единственный.

Отсортируем корзины по количеству яблок (по убыванию). Пусть x яблок в корзине с наибольшим числом яблок, тогда в следующей корзине их не больше x-1, в третьей корзине не больше x-2 и т.д., в последней не больше
x-8. Всего, таким образом, яблок не больше 9x-36. С другой стороны, для того, чтобы положить в первую корзину x яблок, необходимо совершить не менее x действий, и всего в корзинах не менее 6x яблок. Не менее 6x и не более 9x-36 – это одно и то же число. Поэтому 6x9x-36, и 12x. Итак, Вас подходил к корзинам не менее 12 раз, и яблок не менее 72.
Построим пример, показывающий, что 72 яблока в корзинах
оказаться может. Столбцы в таблице – корзины, строки –
подходы Васи к корзинам с 6 яблоками, числа на пересечении
показывают, сколько яблок было в корзине после
соответствующего хода. Нетрудно проверить, что все условия
задачи выполнены: за каждый ход добавляется 6 яблок в 6 разных
корзин, и в конце количество яблок в корзинах разное. Пример
не единственный.
-
|
1 корз.
|
2 корз.
|
3 корз.
|
4 корз.
|
5 корз.
|
6 корз.
|
7 корз.
|
8 корз.
|
9 корз.
|
0 ход
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1 ход
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
2 ход
|
2
|
2
|
2
|
2
|
2
|
2
|
0
|
0
|
0
|
3 ход
|
3
|
3
|
3
|
3
|
3
|
3
|
0
|
0
|
0
|
4 ход
|
4
|
4
|
4
|
4
|
4
|
3
|
1
|
0
|
0
|
5 ход
|
5
|
5
|
5
|
5
|
4
|
3
|
2
|
1
|
0
|
6ход
|
6
|
6
|
6
|
5
|
4
|
3
|
3
|
2
|
1
|
7 ход
|
7
|
7
|
6
|
6
|
5
|
4
|
3
|
2
|
2
|
8 ход
|
8
|
8
|
7
|
7
|
5
|
5
|
3
|
3
|
2
|
9 ход
|
9
|
9
|
8
|
7
|
6
|
5
|
4
|
3
|
3
|
10 ход
|
10
|
10
|
9
|
8
|
6
|
5
|
5
|
4
|
3
|
11 ход
|
11
|
11
|
10
|
9
|
7
|
6
|
5
|
4
|
3
|
12 ход
|
12
|
11
|
10
|
9
|
8
|
7
|
6
|
5
|
4
|
Пусть ab. Тогда ad+bcbd+bc=(c+d)bab. Аналогично разбирается случай ba.
Можно. Сначала разбиваем ящик на части двух видов: 1) со сторонами 10, 30 и 120 см, и 2) со сторонами 10, 40 и 120 см. Как это сделать – показано на рисунке (там изображено разбиение дна ящика 50 х 50 см на прямоугольники 10 х 30 см и 10 х 40 см). Затем каждую из частей разбиваем на кирпичи. Разбиение на рисунке не единственное.

Например, так. Части: 3,5 х 4 см, 2 х 0,5 см и 2 х 0,5 см. Периметры 15, 5 и 5 см. Решение не единственное.
Можно. Рассмотрим правильный 10-угольник. Сумма его углов равна 1800(10-2)=14400, каждый угол равен 1440. Возьмем четыре подряд идущих его вершины (см. рис). Треугольники ABC и BCD тупоугольные, так как их углы (B и C соответственно) являются вершинами десятиугольника и равны по 1440.Тогда остальные углы в этих треугольниках (в силу того, что треугольники равнобедренные) равны по (1800-1440)/2=180. А значит, углы B и D в треугольниках ABD и ACD равны по 1440-180=1260 и все четыре треугольника тупоугольные.

Замечание к решению задачи 9.
Можно взять не только 4, а любое конечное число точек. Для этого следует
рассмотреть правильный n-угольник при больших n и взять его вершины
подряд.
Найдем, сколько всех остальных чисел. Рассмотрим числа от 0 до 999999. Договоримся перед числами, в которых цифр меньше 6, писать столько нулей, чтобы цифр стало по 6. Например, 5242 превратится в 005242 и т.п. На первом месте можно писать любую цифру, кроме 1 (9 возможностей), на втором месте тоже любую цифру, кроме 1 и т.п. Всего чисел 9 х 9 х 9 х 9 х 9 х 9 =96=531441. В связи с тем, что мы рассматривали число 0, которого нет в условии задачи, на самом деле чисел, не содержащих в своей записи единицу, 531440. А чисел единицей 1000000-531440=468560. Ответ: всех остальных чисел больше.
Будем называть число до перестановки цифр большим, а после перестановки – маленьким. Большое число делится на 3, по признаку делимости его сумма цифр делится на 3. Так как после перестановки цифр их сумма не изменилась, сумма цифр маленького числа делится на 3. По признаку делимости маленькое число делится на 3. А значит, большое число, которое в три раза больше, делится на 9.
Повторим круг рассуждений ещё раз. Большое число делится на 9, по
признаку делимости его сумма цифр делится на 9. Так как после перестановки
цифр их сумма не изменилась, сумма цифр маленького числа делится на 9. По
признаку делимости маленькое число делится на 9. А значит, большое число,
которое в три раза больше, делится на 27.
Замечание к решению задачи 11. Нельзя таким же способом доказать, что число
делилось на 81, так как признак делимости на 27 не связан с суммой цифр.
Может. Занумеруем спортсменов по порядку числами от 1 до 100. Ясно, что если номера спортсменов отличаются на 11, то оба они не могут быть одеты в красные костюмы. Разобьем числа от 1 до 100 на группы в зависимости от их остатка при делении на 11.
{1, 12, 23, 34, 45, 56, 67, 78, 89, 100} дают при делении на 11 остаток 1,
{2, 13, 24, 35, 46, 57, 68, 79, 90} дают при делении на 11 остаток 2,
и т.д. Во всех группах, кроме первой, по 9 чисел, а в первой 10. Раскрасим
числа в синий и красный цвет следующим образом: в каждой группе первое
число будет красным, а дальше цвета будут чередоваться. Тогда во всех
группах будет по пять кранных чисел, а всего 55>50. Осталось выдать
спортсменам костюмы в соответствии с раскраской чисел.
Замечание к решению задачи 12.
Можно доказать, что в каждой группе не более 5 спортсменов
могут быть одеты в красные костюмы (для этого спортсменов в
группе надо разбить на пары соседних, например, 1 и 12, 23 и 34 и
т.п.) и, таким образом, всего спортсменов в красных костюмах не
более 55.
x4+x2y2+y4=(x2+y2)2-x2y2=(x2+xy+y2)(x2-xy+y2). Достаточно показать, что при всех x, y, отличных от x=y=1, каждая из скобок больше 1, и, таким образом, число x4+x2y2+y4 имеет делители x2+xy+y2 и x2-xy+y2. Так как x2+xy+y2>x2-xy+y2, достаточно показать, что x2-xy+y2>1.Пусть x=y. Тогда x2-xy+y2=x2>1, так как x=y1. Пусть x>y. Тогда x2-xy+y2=x(x-y)+y2>1, так как каждое из чисел x, x-y, y не меньше 1, а значит, и каждое из чисел x(x-y), y2 не меньше 1. Случай xy.
Пусть суммы равны S. С одной стороны, сумма чисел в таблице равна S+S+S=3S, если считать ее о строчкам. С другой стороны, она равна 1+2+…+9=45. Таким образом, 3S=45 и S=15. Все суммы в строчках, столбцах и на диагоналях равны по 15. Пусть число в центральной клетке равно x. Найдем сумму учетверенного числа в центральной клетке, к которому прибавлены все остальные числа таблицы по одному разу, двумя способами. С одной стороны, она равна 1+2+…+9+3x (все числа взяты по одному разу, а центральное – еще три раза). С другой стороны, искомая сумма равна сумме чисел центральной строке + сумма в центральном столбце + сумма на первой диагонали + сумма на второй диагонали. Получаем равенство 45+3x=15+15+15+15 и находим x=5. Центральное число равно 5. Остальные числа разбиваем на пары. Напротив 1 стоит 9, напротив 2 – 8, ещё две пары составляют 3, 7 и 4, 6. Дальше можно действовать разными способами. Например, докажем, что 9 не может стоять в углу. В самом деле, если 9 в углу, то вместе с ним в одной строке и в одном столбце стоят два числа с суммой 6. Это или 1 и 5, или 2 и 4. Но 5 стоит в центре. Если 2 и 4 стоят в одной строке с 9, тогда нет чисел, которые могут находиться с 9 в одном столбце. Таким образом, 9 стоит на стороне (например, сверху), а 1 – напротив. 2 и 4 все равно которое где стоят в одной строке с 9. Остальные числа легко расставляются из тех соображений, что сумма чисел в строках, столбцах и диагоналях равна 15. Одна из расстановок приведена на рисунке, остальные получаются из нее с помощью поворотов и отражений.
-
Предположим, что из 1 можно получить 811. Рассмотрим числа, которые последовательно получались одно из другого, в обратном порядке. Последним действием не могло быть умножение (так как 811 нечетно), значит, это была перестановка цифр. И перед 811 было 118 или 181. 181 могло получиться тоже только перестановкой цифр, значит, из чисел 118, 181, 811 всех раньше могло появиться только число 118. Рассмотрим число, которое было перед 118 и отличалось от 181, 811. Это могло быть только число 59. Число 59 могло появиться только перестановкой цифр из 95, а число 95 – перестановкой цифр из 59. Итак, если появилось 811, то самым первым числом было 811, 181, 118, 59 или 95. Противоречие тем, что по условию все должно начинаться с 1.
|
 Скачать 491.03 Kb.
Скачать 491.03 Kb.



 . Решим эту систему. Разделив первое уравнение системы на второе, получим
. Решим эту систему. Разделив первое уравнение системы на второе, получим  . Из этой системы находим, что х=3, у=7. Значит, исходная дробь была равна
. Из этой системы находим, что х=3, у=7. Значит, исходная дробь была равна