Математика. 10 класс.
Вырежем из арбуза длинный тонкий цилиндр, протыкающий арбуз насквозь. Это одна из частей, от которой останется две корки. Остальную часть арбуза произвольным образом разрежем на три части, каждая из которых дает по одной корке.
Пусть x – число в верхней левой клетке. Тогда число в нижней левой клетке равно x-6 или x+6, число в нижней правой клетке равно (x-6)/2, 2(x-6), (x+6)/2 или 2(x+6), а число в верхней правой клетке равно (x-6)/2+6, (x-6)/2-6, 2(x-6)+6, 2(x-6)-6, (x+6)/2+6, (x+6)/2-6, 2(x+6)+6 или 2(x+6)-6.
Приравнивая все эти выражения к 2x и к x/2 и решая 16
уравнений, находим единственное решение в натуральных
числах: два противоположных числа равны 6, два остав-
шихся 12.
3.Можно. Решение на рисунке, площадь коробки равна 16.
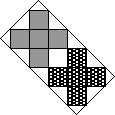
Решим другую задачу. Пусть стороны четырехугольника в порядке обхода a, c, b, d (рисунок слева). Проведем диагональ четырехугольника так, чтобы по одну сторону от нее находились стороны a и c, а по другую – стороны b и d. Тогда площадь первого треугольника равна (ac·sin1)/2, площадь второго треугольника - (bd·sin2)/2, где угол 1 – угол между сторонами a и c, а угол 2 – угол между сторонами b и d. Ввиду того, что синусы не превосходят 1, площадь одного треугольника не больше ac/2, а площадь второго – не больше bd/2. Площадь четырехугольника равна сумме или разности площадей треугольников (разность может получиться, если четырехугольник невыпуклый) и поэтому не превосходит (ac+bd)/2.
Перейдем к решению нашей задачи (рисунок справа). Проведем диагональ
четырехугольника так, чтобы по одну сторону от нее находились стороны b и c,
а по другую – стороны a и d. Отрежем от четырехугольника треугольник,
стороны которого b, c и диагональ. Затем перевернем этот треугольник в
пространстве и приставим так, что диагональ попадет на свое место, а стороны b
и c поменяются местами. Площадь не изменится, так как мы ничего не делали –
только повернули одну из частей! Получили задачу, которую умеем решать.
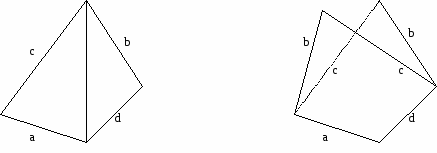
Существуют. Разобьем отрезок длины 8 см двумя точками на три части, имеющие длину (слева направо): 1 см, 4 см, 3 см. Проверим, что среди получившихся длин встречаются все числа 1, 3, 4, 5, 7 и 8. Части 1, 3 и 4 см – это те части, на которые мы разбивали. 8 см – весь отрезок. 5 см – сумма длин левой и центральной частей, и 7 см – центральной и правой. Таким образом, в качестве четырех точек можно взять 2 конца отрезка и 2 точки, которые разбивают его на части.
Определить можно, стоят поровну. Пусть x рублей стоила большая рыбка вчера, y рублей – маленькая рыбка вчера, z рублей – большая рыбка сегодня и t рублей – маленькая рыбка сегодня.
Тогда 3z+t=5x, 2z+t=3x+y. Требуется сравнить z+2t и 5y. Сравним:
5y=5(3x+y)-3·5x=5(2z+t)-3(3z+t)= z+2t.
7.Можно. Одно из возможных расположений на рисунке.
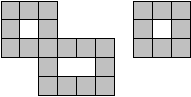
Из соображений площади можно делать вывод: не получится вырезать больше, чем 33 прямоугольника (так как 34·5>13·13). Вырезать 33 прямоугольника можно так: разбить квадрат на центральную часть (квадрат 7 х 7) и каемку. Каемку разбить на 4 прямоугольника 3 х 10, а каждый из них на 6 прямоугольников 1 х 5. Центральный квадрат 7 х 7 разбить на прямоугольник 7 х 5, из которого можно вырезать 7 прямоугольников 1 х 5, и на прямоугольник 7 х 2, из которого можно вырезать 2 прямоугольника 1 х 5.
Стороны нескольких прямоугольников параллельны осям координат. Любые два из них имеют общую точку. Докажите, что все они имеют общую точку.
Рассмотрим отрезки - проекции прямоугольников на ось Ox. Докажем, что они имеют общую точку. В самом деле, каждая точка – левый конец проекции лежит левее, чем правый конец другой проекции (если бы это было не так, то прямоугольники, которые дают такие проекции, не пересекались бы). Рассмотрим любую точку (назовем ее X) на отрезке между самым правым из левых концов проекций и самым левым из правых концов. В каждом прямоугольнике найдется точка, абсцисса которой равна X. Аналогично рассматриваются проекции на ось Oy и строится точка Y такая, что все прямоугольники имеют точки с ординатой, равной ординате точки Y. Таким образом, точка с той же абсциссой, что и X, и с той же ординатой, что и Y, искомая.
25 столкновений. Представим себе, что на всех шариках, летящих слева, установлены телепорты – устройства, позволяющие им проходить мгновенно сквозь правые шарики. Пусть шарик слева летит со скоростью v и шарик справа летит со скоростью v. В обычной ситуации после столкновения левый шарик будет удаляться от места столкновения влево со скоростью v, а правый – вправо с той же скоростью. В случае телепортации будет то же самое, только шарики поменяются местами. Если шарики неотличимы друг от друга и нам показывают фильм о шариках, мы не можем отличить столкновения от телепортаций. Поэтому все будет одинаково, в частности количество столкновений равно количеству телепортаций.
Подсчитаем телепортации. Каждый из 5 левых шариков должен пройти
сквозь каждый из 5 правых. 5·5=25.
n3+5n=(n3-n)+6n=(n-1)n(n+1)+6n. Второе слагаемое делится на 6. Докажем, что первое тоже делится на 6. В самом деле, числа n-1, n, n+1 дают разные остатки при делении на 3, значит, какое-то из них на 3 делится (проверить это можно так: первый случай, n=3k, тогда n делится на 3; второй случай, n=3k+1, тогда n+2=(3k+1)+2=3(k+1) делится на 3; третий случай, n=3k+2, тогда n+1=(3k+2)+1=3(k+1) делится на 3). Из чисел n и n+1 одно четно (рассмотрите случаи четного и нечетного n). Таким образом, из трех множителей, входящих в (n-1)n(n+1), хотя бы одно делится на 2 и хотя бы одно делится на 3. Значит, их произведение (n-1)n(n+1) делится на 2 и на 3, т. е. на 6.
Пусть второе число равно x. Тогда третье число, составляющее в сумме с 1 число x, равно x-1. Аналогично рассуждая, получаем четвертое число –1, пятое –x, шестое 1-x, седьмое 1, восьмое x и т. д. В последовательности чисел имеется период, его длина равна 6. 2005 при делении на 6 дает остаток 1. 2005-е число равно первому и равно 1.
13. Назовем серией прямых любую из проведенных прямых и все, ей
параллельные. Докажем, что все серии содержат поровну прямых. От
противного. Пусть прямых, параллельных прямой a, x штук, а прямых,
параллельных b, y штук, yx, а всего z прямых. Тогда прямая a пересекает все прямые, кроме прямых из своей серии, т. е. z-x штук. Аналогично прямая b пересекает все прямые, кроме своей серии, т. е. z-y штук. Так как по условию z-x=2004=z-y, то x=y.
Пусть в каждой серии k прямых, а всего серий n. Тогда каждая прямая пересекает k(n-1) прямую.
k(n-1)=2004. Всего прямых kn=k(n-1)+k=2004+k, где k – обязательно делитель числа 2004 ввиду того, что k(n-1)=2004. 2004=22·3·167, 167 – простое. У числа 2004 двенадцать делителей: это 1, 2, 3, 4, 6, 12 и все эти числа, умноженные на 167. В задаче 12 ответов: 2004+1, 2004+2, 2004+3, 2004+4, 2004+6, 2004+12, 2004+167, 2004+334, 2004+501, 2004+668, 2004+1002, 2004+2004.
14. Рассмотрим четыре самых маленьких числа. Их сумма положительна, поэтому среди них есть положительное число. Но отсюда следует, что остальные 13 чисел положительны. А сумма всех 17 чисел равна положительной сумме 13 чисел плюс положительная сумма четырех чисел.
15.Не может. От противного. Тогда дружинник A должен побывать на дежурстве с 99 остальными, т. е. выйти на дежурство 99/2=49,5 раз – нецелое число.
Математика. 11 класс.
Если альпинисту останется путь 100 метров и у него будет 100 метров веревки, он прикрепляет один конец веревки и спускается по ней.Если у альпиниста 150 метров веревки и он находится на верхней площадке (остался путь 200 метров), он должен разрезать веревку на части 100 и 50 метров. 50-метровую веревку надо одним концом прикрепить к площадке, а на другом конце сделать петлю, через которую продернуть половину оставшейся 100-метровой веревки. Затем спуститься на площадку на высоте 100 метров от земли и выдернуть 100-метровую веревку для последнего этапа спуска.
Если у альпиниста 175 метров веревки и он на вершине скалы, он разрезает веревку на
части 25 и 150 метров, первую прикрепляет к скале и делает петлю, вторую пропускает
через петлю и спускается на 100 метров. Выдергивает 150-метровую веревку и
приступает ко 2 и 3 этапам спуска. Лишние 5 метров веревки даны в задаче для того,
чтобы была возможность вязать узлы и петли.
Найдём произведение чисел в каждом из четырех квадратов 2 х 2, а затем такие произведения перемножим. Получим 16. В произведение 16 угловые числа вошли как множители по одному разу (они участвовали при вычислении какого-то одного произведения в квадрате 2 х 2), число в центре четыре раза, остальные по два. Разделим это произведение (16) на произведение чисел первой строки, затем на произведение чисел второй троки, затем на произведение чисел третьей строки. Получим 16, оно равно третьей степени центрального числа, умноженной на числа на сторонах. Затем разделим то, что осталось, на произведение чисел во второй строке, и на произведение чисел во втором толбце. Получится 16, это и есть центральное число.
-
abde=2, bcef=2, dexy=2, efyz=2, (abde)(bcef)(dexy)(efyz)=16,
ab2cd2e4f2xy2z=16.
abc=1, def=1, xyz=1, (ab2cd2e4f2xy2z)/((abc)(def)(xyz))=16,
bde3fy=16.
def=1, bey=1, (bde3fy)/((def)(bey))=16, e=16.
Пусть X – середина AB, Y – середина BC. Тогда DX – медиана в прямоугольном треугольнике ADB из вершины прямого угла, она равна половине гипотенузы AB. Аналогично, YE – половина BC. В треугольнике ABC XY – средняя линия, равная половине стороны AC. Итак, полупериметр равен (AB+AC+BC)/2=DX+XY+YEDE, так как если какая-то из точек X, Y не лежит на DE, то ломаная длиннее отрезка, соединяющего ее концы.
Не обязательно. Если разрезать квадрат со стороной 2/3 на два равных прямоугольника, периметр каждого будет равен 2, а периметр квадрата 8/3. Пример не единственный.
Нельзя. Сумма чисел сначала 21, а затем на каждом шаге изменяется на 2. Поэтому сумма чисел в любой момент нечетна. Если в какой-то момент числа равны, то сумма шести равных чисел делится на 6 и поэтому четна. Противоречие.
Да, такое возможно. Один из примеров: пусть путешественник вышел в полдень, и в периоды времени 12.00-12.30, 13.00-13.30, 14.00-14.30, 15.00-15.30 шел со скоростью 8 км/ч, проходя за каждые полчаса по 4 км. В остальные периоды 12.30-13.00, 13.30-14.00, 14.30-15.00 он шел со скоростью 2 км/ч, проходя за полчаса по 1 км. Тогда за 3,5 часа он прошел 19 км.
Докажем, что за каждый час путешественник проходил по 5 км. Если мы начинаем
отсчитывать час от 12.00, 12.30, 13.00, 13.30, 14.00 или 14.30, то такой час состоит из
получаса «быстрой ходьбы» и получаса «медленной ходьбы». Идя быстрым шагом,
путешественник проходит 4 км, а медленным – 1 км, всего, таким образом, получается
5 км. Пусть час начинается в другое время (например, можно рассматривать промежуток
длительностью в час между 14.12 и 15.12 и т.п.). Тогда он содержит внутри себя или
получас «быстрой ходьбы», или получас «медленной ходьбы». В первом случае начало и
конец рассматриваемого нами промежутка длительностью в час – это периоды
«медленной ходьбы», в сумме они составляют 1 час – 30 минут = 30 минут. Т. е. в течение
часа половину времени путешественник идет быстро, половину медленно. Всего, как мы
уже читали, получается 5 км. Второй случай разбирается аналогично.
Можно. Например, его координаты (0, 0), (12, 16), (-12, 9). Длины сторон 15, 20 и 25. Он прямоугольный (проверим теорему Пифагора).
Один из примеров на рисунке. Сумма длин дорог 2+45<11.
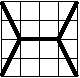
Один из примеров следующий. В треугольнике отмечаем вершины, основания высот и точку пересечения высот. В качестве прямых возьмем стороны и высоты. Нетрудно проверить, что все точки и прямые, кроме оснований высот, удовлетворяют условию. Через основания высот проходит только по две отмеченные прямые. Проведем через них ещё по одной прямой так, чтобы три вновь построенные прямые были параллельны между собой и не параллельны остальным отмеченным линиям. Параллельно перенесем треугольник 2 раза на векторы, направленные параллельно трем построенным прямым. Полученные 21 точка и 21 прямая удовлетворяют условию.
Пятизначных четных чисел 45000, так как на первом месте может стоять любая из 9 цифр (кроме 0), на втором, третьем и четвертом – любые цифры, а на пятом – любая из пяти четных цифр. Пятизначных четных чисел без троек 8·93·5=29160. Ответ: 15840.
11. Можно. Например, так, как показано на рисунке.
2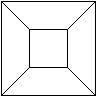 30 30
42 3
7 105
5
Ни одна из диагоналей не проходит через центр многоугольника. Докажем это. Центр многоугольника совпадает с центром описанной окружности. Если диагональ проходит через центр, она лежит на прямой, содержащей диаметр описанной окружности. Но диаметр не может проходить через две вершины многоугольника, так как 2005 – нечетное число: по одну сторону от диаметра окажется x дуг окружности, на которые она разбивается вершинами, по другую 2005-x, и x2005-x. Значит, центр описанной окружности лежит в одном из треугольников. Именно этот треугольник остроугольный, а остальные тупоугольные. В самом деле, центр описанной окружности лежит внутри остроугольных треугольников, на гипотенузе прямоугольных и вне тупоугольных. А описанные окружности для каждого треугольника совпадают с окружностью, описанной около многоугольника.
.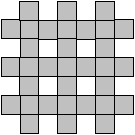
13.Наименьшее число частей – 15. Примеров с 15 частями много. Один из них: три вертикальных прямоугольника 1 х 7 и 12 квадратиков 1 х 1.
Раскрасим клетки фигуры в черный и белый цвет в шахматном порядке. Клеток одного цвета 24, другого 9, значит, какого-то из цветов больше на 15 клеток. Но все прямоугольники имеют ширину 1 и площадь белого отличается от площади черного не более, чем на 1. Таким образом, меньше, чем на 15 прямоугольников, не разрезать.
14.Всего кругов было столько, сколько кругов сделали стрелки, т. е. 720+12+1=733. Так как ни одна из мух не обгоняла другую (проверьте!), любые две мухи проехали одинаковое число кругов или число кругов, отличающееся на 1. 733=245+244+244. Муха, которая вначале сидела на секундной стрелке, проехала 245 кругов, а две другие по 244.
. 15. a2+b2+c2=(a+b+c)2-2(ab+ac+bc)=25-14=11.
Такие числа действительно существуют: один из примеров a=3, b=c=1.
|
 Скачать 491.03 Kb.
Скачать 491.03 Kb.
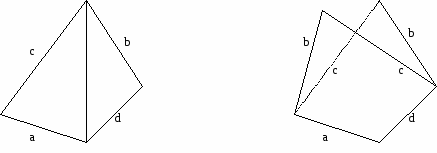


 30
30