Планирование курса «Математика»
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
| СОДЕРЖАНИЕ ОБУЧЕНИЯ алгебра 9 класс 1. Свойства функций. Квадратичная функция Функция. Свойства функций. Квадратный трехчлен. Разло жение квадратного трехчлена на множители. Функция у = ах2 + bх + с, ее свойства и график. Степенная функция. Основная цель — расширить сведения о свойствах функ ций, ознакомить учащихся со свойствами и графиком квадратич ной функции. В начале темы систематизируются сведения о функциях. По вторяются основные понятия: функция, аргумент, область опре деления функции, график. Даются понятия о возрастании и убы вании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа. Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квад ратного трехчлена, разложении квадратного трехчлена на мно жители. Изучение квадратичной функции начинается с рассмотрения функции у = ах2, ее свойств и особенностей графика, а также других частных видов квадратичной функции — функций у = ах2 + b, у = а (х - т)2. Эти сведения используются при изуче нии свойств квадратичной функции общего вида. Важно, чтобы учащиеся поняли, что график функции у = ах2 + bх + с может быть получен из графика функции у = ах2 с помощью двух па раллельных переносов. Приемы построения графика функции у = ах2 + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у учащих ся умения указывать координаты вершины параболы, ее ось сим метрии, направление ветвей параболы. При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функ ции, а также промежутки, в которых функция сохраняет знак. Учащиеся знакомятся со свойствами степенной функции у=хп при четном и нечетном натуральном показателе п. Вводит ся понятие корня п-й степени. Учащиеся должны понимать смысл записей вида 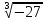 , ,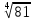 Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
Целые уравнения. Дробные рациональные уравнения. Нера венства второй степени с одной переменной. Метод интервалов. Основная цель — систематизировать и обобщить сведе ния о решении целых и дробных рациональных уравнений с од ной переменной, сформировать умение решать неравенства вида ах2 + bх + с > 0 или ах2 + bх + с < 0, где а ≠0. В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия це лого рационального уравнения и его степени. Учащиеся знако мятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспо могательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться в дальнейшем при решении тригонометрических, логарифмиче ских и других видов уравнений. Расширяются сведения о решении дробных рациональных уравнений. Учащиеся знакомятся с некоторыми специальными приемами решения таких уравнений. Формирование умений решать неравенства вида ах2 + bх + с > 0 или ах2 + bх + с < 0, где а ≠ 0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы, ее расположение относительно оси Ох). Учащиеся знакомятся с методом интервалов, с помощью ко торого решаются несложные рациональные неравенства.
Уравнение с двумя переменными и его график. Системы урав нений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы. Основная цель — выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя перемен ными, и текстовые задачи с помощью составления таких систем. В данной теме завершается изучение систем уравнений с дву мя переменными. Основное внимание уделяется системам, в ко торых одно из уравнений первой степени, а другое второй. Из вестный учащимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к реше нию квадратного уравнения. Ознакомление учащихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограни чиваться простейшими примерами. Привлечение известных учащимся графиков позволяет при вести примеры графического решения систем уравнений. С помо щью графических представлений можно наглядно показать уча щимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений. Разработанный математический аппарат позволяет сущест венно расширить класс содержательных текстовых задач, решае мых с помощью систем уравнений. Изучение темы завершается введением понятий неравенства с двумя переменными и системы неравенств с двумя переменными. Сведения о графиках уравнений с двумя переменными использу ются при иллюстрации множеств решений некоторых простей ших неравенств с двумя переменными и их систем.
Арифметическая и геометрическая прогрессии. Формулы п-го члена и суммы первых п членов прогрессии. Бесконечно убываю щая геометрическая прогрессия. Основная цель — дать понятия об арифметической и гео метрической прогрессиях как числовых последовательностях осо бого вида. При изучении темы вводится понятие последовательности, разъясняется смысл термина «п-й член последовательности», вы рабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий. Работа с формулами п-го члена и суммы первых п членов про грессий, помимо своего основного назначения, позволяет неодно кратно возвращаться к вычислениям, тождественным преобразо ваниям, решению уравнений, неравенств, систем. Рассматриваются характеристические свойства арифметиче ской и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.
Комбинаторное правило умножения. Перестановки, размеще ния, сочетания. Относительная частота и вероятность случайного события. Основная цель — ознакомить учащихся с понятиями пе рестановки, размещения, сочетания и соответствующими форму лами для подсчета их числа; ввести понятия относительной час тоты и вероятности случайного события. Изучение темы начинается с решения задач, в которых требу ется составить те или иные комбинации элементов и подсчитать их число. Разъясняется комбинаторное правило умножения, ко торое используется в дальнейшем при выводе формул для подсче та числа перестановок, размещений и сочетаний. При изучении данного материала необходимо обратить внимание учащихся на различие понятий «размещение» и «сочетание» сформировать у них умение определять, о каком виде комбинаций идет речь в задаче. В данной теме учащиеся знакомятся с начальными сведения ми из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание учащихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными. 6. Повторение 9 класс
СОДЕРЖАНИЕ ОБУЧЕНИЯ геометрия 8 класс 1. Четырехугольники Многоугольник, выпуклый многоугольник, 'четырехуголь ник. Параллелограмм, его свойства и признаки. Трапеция. Пря моугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии. Основная цель — изучить наиболее важные виды четы рехугольников — параллелограмм, прямоугольник, ромб, квад рат, трапецию; дать представление о фигурах, обладающих осе вой или центральной симметрией. Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства тре угольников, поэтому полезно их повторить в начале изучения темы. Осевая и центральная симметрии вводятся не как преобразо вание плоскости, а как свойства геометрических фигур, в част ности четырехугольников. Рассмотрение этих понятий как дви жений плоскости состоится в 9 классе.
Понятие площади многоугольника. Площади прямоуголь ника, параллелограмма, треугольника, трапеции. Теорема Пи фагора. Основная цель — расширить и углубить полученные в 5—6 классах представления учащихся об измерении и вычисле нии площадей; вывести формулы площадей прямоугольника, па раллелограмма, треугольника, трапеции; доказать одну из глав ных теорем геометрии — теорему Пифагора. Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квад рата, обоснование которой не является обязательным для уча щихся. Нетрадиционной для школьного курса является теорема об от ношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство призна ков подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади. Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора. Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треуголь ника. Основная цель — ввести понятие подобных треугольни ков; рассмотреть признаки подобия треугольников и их примене ния; сделать первый шаг в освоении учащимися тригонометриче ского аппарата геометрии. Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорцио нальность сходственных сторон. Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу. На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных от резках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение. В заключение темы вводятся элементы тригонометрии — си нус, косинус и тангенс острого угла прямоугольного треуголь ника.
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. Основная цель — расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, свя занные с окружностью; познакомить учащихся с четырьмя заме чательными точками треугольника. В данной теме вводится много новых понятий и рассматрива ется много утверждений, связанных с окружностью. Для их усво ения следует уделить большое внимание решению задач. Утверждения о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах бис сектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения сере динных перпендикуляров. Наряду с теоремами об окружностях, вписанной в треуголь ник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного че тырехугольника.
8 класс
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||