«Преобразование графиков функции»

Скачать 27.67 Kb. Название «Преобразование графиков функции» Дата 18.04.2016 Размер 27.67 Kb. Тип Документы

Гимназия №125 Урок-презентация в 8 классе по теме: «Преобразование графиков функций» Учитель: Церетели Н.К. Декабрь, 2008 г. Тема: «Преобразование графиков функции». Цель: Повторить понятия функции и графика, рассмотреть свойства функции, преобразования графиков. Рассмотреть применение графиков при решении уравнений и системы уравнений. Ход урока: 1. Организационный момент. 2. Актуализация знаний. Что называется функцией? Какая переменная называется зависимой и независимой? Как обозначается функция? Какие примеры функций вы знаете? Что называется графиком? 3. Историческая справка. Понятие функции заложили в XII веке французские учёные Франсуа Виет и Рене Декарт. Они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение неизвестных : x, y, z, известных: a,b,c. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие изменения. Тем самым появилась возможность записывать общие формулы. Само слово «функция» (совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673 году. (Под функцией он понимал отрезок, длина которого меняется по какому-нибудь определённому закону.) В России понятие функции ввёл Н. Лобачевский, он рассматривал вопросы исследования функции. Создал учебник «Алгебра или вычисление конечных». Сегодня на уроке мы будем отрабатывать навыки в построении графиков функции и будем описывать свойства функции по графику. Но, сначала, мы должны хорошо разобраться в процессе построения графиков функции. Как построить график функции? Каковы правила преобразования графиков? 4. Просмотр презентации с объяснением правил преобразования графиков квадратичной функции. (Приложение 1) 5. Аналогично, сформулируйте правила преобразования графика обратной пропорциональности. Назовите уравнения функции по готовым чертежам. (Приложение 2) 6. Выполнение построения графиков. (Работа по рядам.) Схематически изобразить графики функций. (Приложение 3) Проверить и оценить работу.-2х Что называется кусочной функцией? Построить график функции: Устно перечислить свойства: область определения функции область значения функции промежутки возрастания и убывания функции точки пересечения с осью абсцисс и осью ординат. Самостоятельная работа. Решить графически уравнения: 1 вариант : 3х2-6х-4=2х-4 2 вариант: -х2-2х+4=х-2 Итог урока: обобщение знаний; оценки. Приложение 2 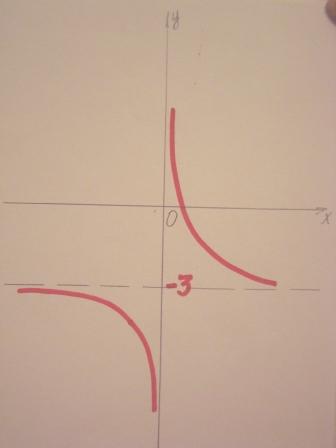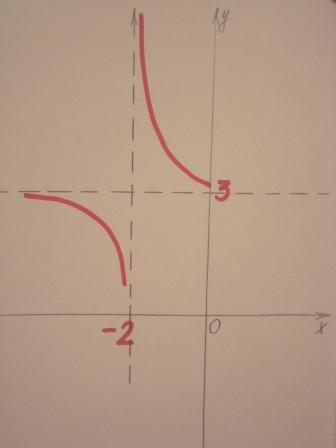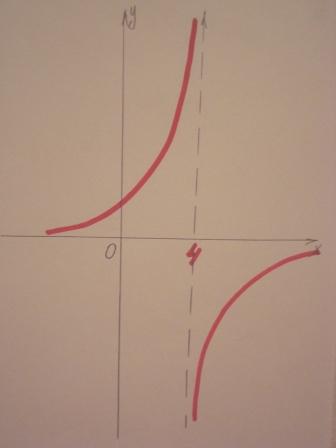Приложение 3 1 ряд 2 ряд 3 ряд у=5х+3 у=-2х+3 у=4х-3 у=-6х2 у=3х2 у=7х2 у=5(х-3)2 у=-3(х+1)2 у=2(х-3)2 у=7х2+3 у=-х2-4 у=2х2-2 у=5/х у=-7/х у=3/х у=1/(х-3) у=-1/(х+2) у=-1/(х-4) у=-3/х+9 у=2/х+3 у=-4/х-7 у=6/(х+1)-7 у=-1/(х-2)+3 у=2/(х-3)+4