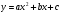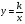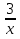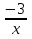Самостоятельная работа на компьютере: построение графиков. Обсуждение результатов. Домашнее задание. Ход урока: Организационный момент
 Скачать 122.91 Kb. Скачать 122.91 Kb.
|
  Цели урока: Цели урока: Обучающая: закрепление навыков исследования функций и построения графиков прямой, параболы и гиперболы. Построение графиков функций в среде электронных таблиц;обобщениеи систематизация знаний о свойствах функций. Развивающая: развитие логического мышления,формирование поискового стиля мышления, умение сравнивать, анализировать, делать выводы. Воспитательная: воспитание усидчивости, внимания; привитие учащимся навыков самостоятельной работы, бережного отношения к оборудованию. Тип урока: обобщающий урок. Вид урока: урок теоретических и практических работ исследовательского типа. Форма работы: классно-урочная. Технология: личностно-ориентированная; проблемно-исследовательская, информационно коммуникационная. Время проведения: 2014 год. Оборудование: компьютерный класс, мультимедийный проектор. План урока: 1. Организационный момент. 2. Сообщение темы и постановка цели урока. 3.Фронтальный опрос для проверки уровня подготовки учащихся по свойствам графиков прямой, параболы и гиперболы. 4. Актуализация знаний по построению диаграмм и графиков с помощью табличного процессора Excel 5. Практическая самостоятельная работа на компьютере: построение графиков. 6. Обсуждение результатов. 7. Домашнее задание. Ход урока: 1. Организационный момент. Приветствие. 2. Сообщение темы и постановка цели урока. В первой части итоговой письменной работы чаще всего представлены задания, требующие установить соответствие между графиком и формулой, задающей функцию. Среди графиков функций встречаются прямые, параболы и гиперболы. Для выполнения заданий по этой теме из любой части работы полезно знать уравнения и свойства этих функций. Сегодня на уроке мы повторим и обобщим этот материал. Мотивация. Вы знаете, что для построения графиков вручную требуется много времени, приходится выполнять достаточно много вычислений, заполнять таблицу значений аргумента и функции. Поэтому сегодня мы будем строить графики с помощью табличного процессора MS Excel, который по нашей команде выполнит вычисления и построит графики. Нашей задачей будет повторение уравнений прямой, параболы и гиперболы, а также закрепление знаний по основным свойствам этих функций. 3. Фронтальный опрос для проверки уровня подготовки учащихся по свойствам графиков прямой, параболы, гиперболы. Перечень вопросов и ответов для фронтального опроса и повторения.
100% - 60% 28 тонн – x тонн 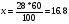 Ответ: 16.8 тонн. Ответ: 16.8 тонн.
Решение: 3 мин. – 270 коробок 10 мин. – x коробок x=(270*10)/3=900
Решение: r=q*pr=(85-5p)*p 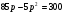 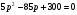 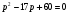 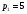 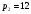 . Ответ: 12 . Ответ: 12
Решение: Пусть x(метров) ширина участка, тогда длина (x+7)метров, а площадь участка (x+7)*x. Составим и решим уравнение: (x+7)*x=120 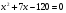 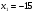 не является решением. не является решением.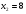 - ширина, тогда длина участка x+7=15 - ширина, тогда длина участка x+7=15Ответ: Длина участка 15 метров.
Решение: 3 – 14 человек x – 21 человек. 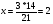 Ответ: за 2 дня.
Решение: 15 рейсов – 4 тонны xрейсов – 6 тонн x=(15*4)/6=10 рейсов. 4. Актуализация знаний по построению диаграмм и графиков с помощью табличного процессора Excel Метод повторения – словесно-иллюстративный в форме практического занятия с использованием интерактивной доски. Ввод формулы начинается со знака «=». Формулы содержат числа, имена ячеек, знаки операций, круглые скобки, имена функций. Формула пишется в одну строку, символы выстраиваются последовательно друг за другом, проставляются все знаки операций. Повторим знаки операций: + сложение, - вычитание; * умножение; / деление;^ возведение в степень. Для распространения данных и формул используется маркер заполнения, для этого: 1. Выделите ячейку (или две соседние ячейки для распространения значений с заданным интервалом) 2. Установите указатель в правый нижний угол и, когда он примет вид тонкого черного креста, удерживая нажатой левую клавишу мыши, перетащите его в нужном направлении. Алгоритм построения графиков функций в табличном процессоре Excel: 1 . Ввести значение аргумента с заданным промежутком. 2. Ввести формулу (уравнение функции) 3. Распространить данные и формулу с помощью маркера заполнения. 4. Построить график функции (вставка – диаграмма – точечная), выделив диапазон значений. 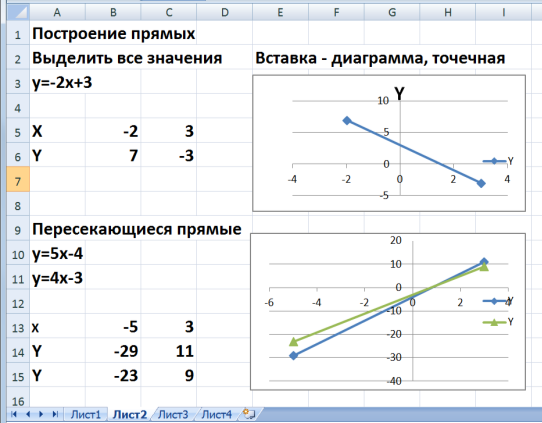 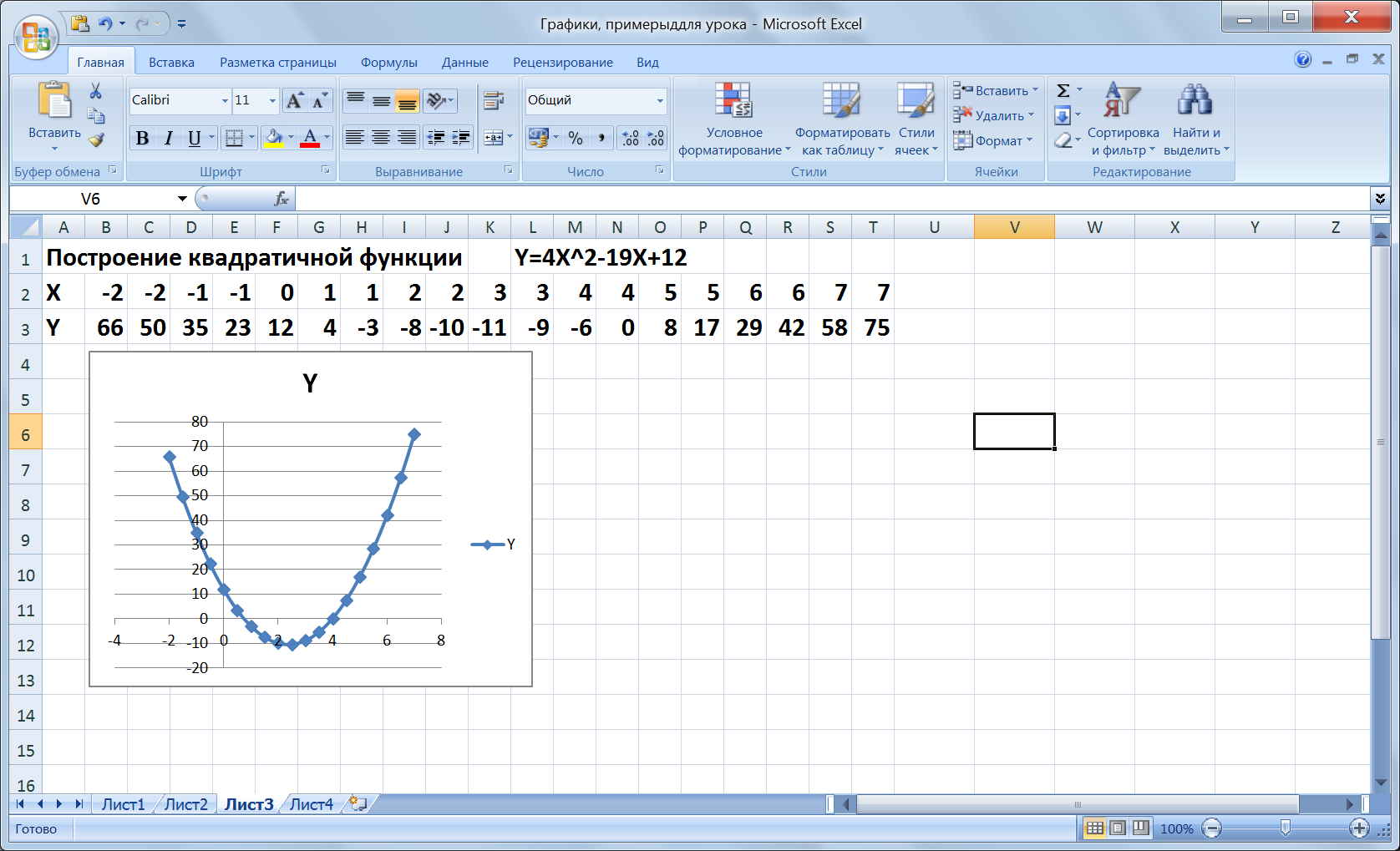 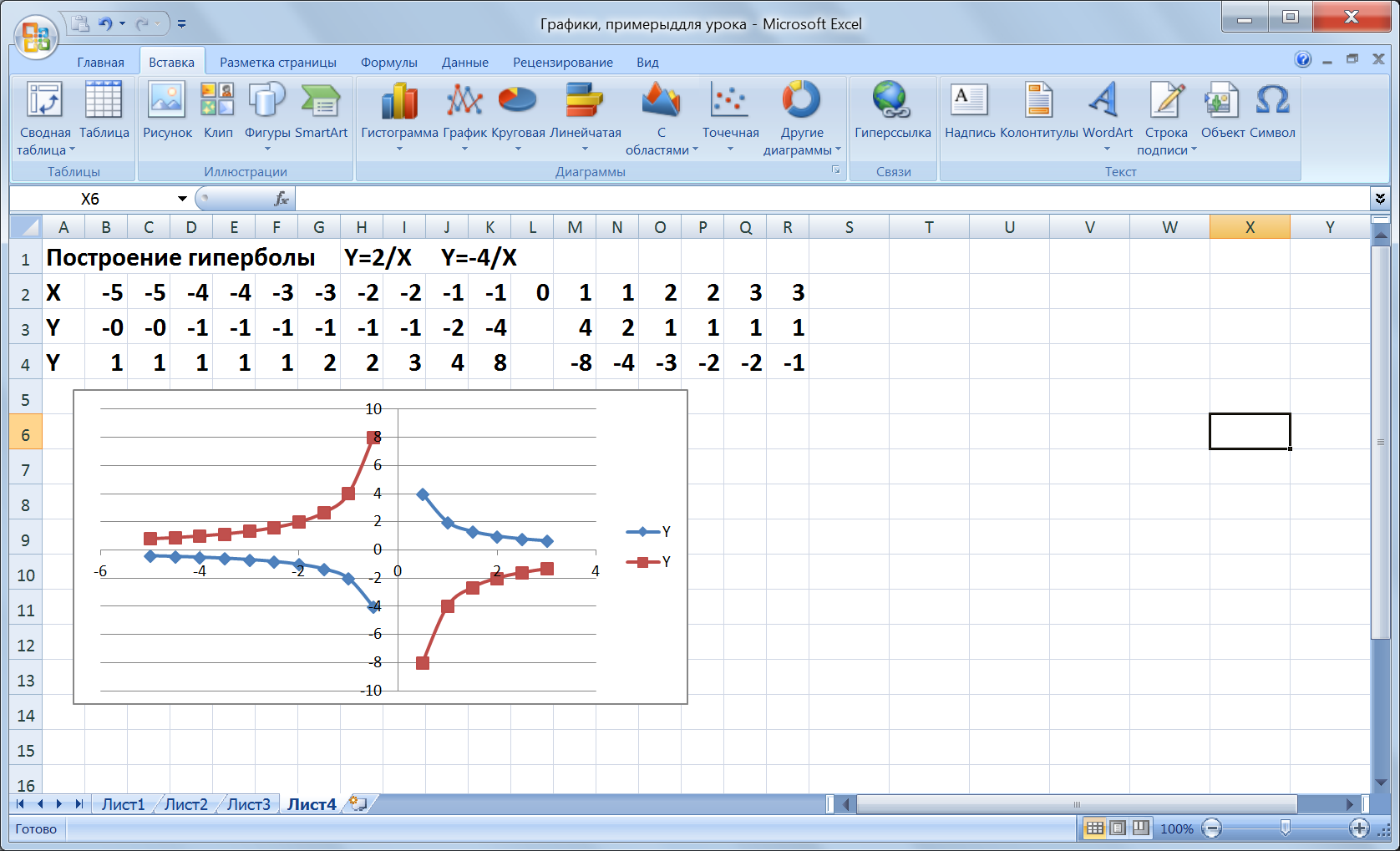 5. Практическая самостоятельная работа на компьютере: построение графиков прямой, параболы и гиперболы. Задания для работы и результаты работы учащихся передаются по локальной сети на сервер преподавателя. Задания дифференцированы по сложности. Учащиеся работают в индивидуальном режиме. Используя сетевые ресурсы,преподавательконтролирует работу учащихся на всех этапах. Примеры заданий.
6. Обсуждение результатов. Сравнить результаты построения графиков на компьютере и вручную. Оправдано ли при построении данных графиков и применение компьютера? Сделать выводы. Анализ полученных результатов. Выставление комплексных оценок: за фронтальный опрос и практическую работу. 7. Домашняя работа.Повторение общей схемы исследования функции и построения ее графика.Результаты занести в таблицу.
Список литературы и Интернет-ресурсов:
|