«Повышение мотивации и качества знаний учащихся по математике на основе личностно ориентированного подхода»
 Скачать 415.26 Kb.
|
| Содержание образования Содержание образования рассматривается как педагогически адаптированный социальный опыт человечества, тождественный по структуре мировой культуре. В соответствии с таким пониманием содержание образования должно включать, помимо «готовых» знаний и опыта осуществления деятельности по образцу, также опыт творческой деятельности и эмоционально-ценно стных отношений. Определены и обоснованы принципы формирования содержания обучения при личностно —ориентированном подходе к образованию: свобода выбора содержания учителем и учениками, открытость, учет единства синхронического и диахронического подходов при формировании содержания, учет единства сознательной и бессознательной составляющих в культуре и в представлениях учеников. Принцип свободы выбора содержания обучения позволяет учащимся реализовать свои образовательные потребности в разных образовательных областях в соответствии с собственными возможностями. Свой выбор они осуществляют осознанно, взвешивая собственные интересы и возможности, сравнивая программы и методы работы учителей. Процесс образования начинает приобретать для них личную значимость. Как показывает опыт формирования содержания обучения при личностно — ориентированном подходе к образованию, доступность дидактических материалов , рабочих программ, ученикам позволяет, с одной стороны, реализовывать принципы формирования содержания обучения при личностно — ориентированном подходе к образованию, а с другой стороны, обогащает арсенал дидактических материалов учителя, позволяя тем самым разнообразить образовательную среду для учеников. Сущностными характеристиками содержания обучения при личностно —ориентированном подходе к образованию являются свойства целостности, актуальности, проблемности содержания обучения. Сегодня, в соответствии с современными целями в содержании образования (в любой его конкретной форме - учебный план, программа, учебник, календарно-тематический план, план урока и т.д.) выделяется как минимум три компонента: предметный, технологический и субъективный (согласно терминологии В.В.Серикова). Названия этих компонентов у разных авторов формулируются по-разному, но общий смысл остается: знания о мире, знания о познании, знания о познающем. Для того, чтобы при конструировании содержания урока удержать в поле зрения все образовательные цели и включить все три компонента содержания образования, при личностно-ориентированном подходе часто используется технология задачного подхода, алгоритм которой разработан профессором В.В.Сериковым. 1. Решить предметную задачу - определить объем учебного материала (обязательного и дополнительного), выяснить логику его изложения и структуру. Основание отбора - обязательный минимум (государственный образовательный стандарт), образовательная программа. "Наращивание” инновационного предметного содержания возможно по соображениям гуманитаризации, интеграции, регионализации, экологизации с привлечением новых данных науки и другим. 2. Решить конструктивную задачу : а) определить способы приобщения учащихся к данной области культуры, возможности перевода содержания учебного материала из предметной сферы в коммуникативно-деятельностную. То есть определить блоки в учебном материале и способы, с помощью которых будет организована работа учащихся по интерпретации и усвоению этих блоков. б) определив способы переработки учащимися учебного материала (то есть методику их работы), рассмотреть возможность переноса этих способов из методики урока в содержание урока, то есть организовать анализ способов деятельности и познания. 3. Решить личностно ориентированную задачу - определить ценностносмысловой компонент выделенного учебного материала, то есть возможные связи учебного материала с ценностно-смысловой сферой учащихся, их жизненными ценностями, проблемами, интересами, затем определить способы организации рефлексии. Разработка индивидуальных образовательных программ (в отличии от учебного стандарта), способствующих коррекции, стимулу, прогнозу личностного развития является обязательной для каждого учителя. Цель дидактического материала, применяемого на личностно ориентированном уроке , состоит в том, чтобы отработать учебную программу, обучит учащихся необходимым знаниям, умениям, навыкам. Виды дидактического материала: учебные тексты, карточки-задания, дидактические тесты. Задания разрабатываются по тематике, по уровню сложности, по цели использования, по количеству операций на основе разноуровневого дифференцированного и индивидуального подхода с учетом ведущего типа учебной деятельности учащегося (познавательная, коммуникативная, творческая). В основе такого подхода лежит возможность оценки по уровню достижения в овладении знаниями, умениями, навыками. Я распределяю карточки среди учеников, зная их познавательные особенности и возможности, и не только определяю уровень овладения знаниями, но и учитываю личностные особенности каждого ученика, создавая оптимальные условия для его развития путем предоставления выбора форм и способов деятельности. По рекомендациям И.С. Якиманской и В.В. Серикова для дидактического обеспечения личностно-ориентированного подхода необходимо следующее: - учебный материал должен быть субъективно значим для ученика и его усвоения, организация учебной деятельности должна учитывать актуальный уровень его развития; - систематически стимулировать ученика к самоценной образовательной деятельности, которая переходила бы в самообразование, саморазвитие; - учебный материал следует организовывать таким образом, чтобы у ученика оставалось право выбора, возможность выбора учебных задач, заданий; - всячески поощрять учащихся и стимулировать их к самостоятельному выбору наиболее приемлемых для них способов проработки учебного материала; - особое внимание уделять формированию общеучебных умений с учетом особенностей и индивидуальных способностей ученика; - не только оценивать конечный результат учебной деятельности ученика, но и формировать самоконтроль самого процесса учения, активизировать рефлексию мышления. Формы и методы учебно-воспитательной работы «Главная особенность процесса усвоения состоит в его активности: знания можно передать только тогда, когда ученик их берёт, то есть выполняет… какие-то действия с ними. Другими словами, процесс усвоения знаний – это всегда выполнение учащимися определённых познавательных действий». Н. Ф. Талызина Поиск различных форм организации учебной деятельности, методов и приемов обучения, влияющих на развитие самостоятельности учащихся, является одной из основных задач учителя. Использование на уроках математики приёмов и методов, активизирующих учебно - познавательную деятельность обучающихся, существенно повышает уровень знаний по предмету, творческую и познавательную активность детей. Деятельность учителя на уроке с личностно-ориентированной направленностью имеет свою специфику. 1. Создание положительного эмоционального настроя на работу всех учеников в ходе урока. 2. Сообщение в начале урока не только темы, но и организации учебной деятельности в ходе урока. 3. Применение знаний, позволяющих ученику самому выбирать тип, вид и форму материала (словесную, графическую, условно-символическую). 4. Использование проблемных творческих заданий. 5. Стимулирование учеников к выбору и самостоятельному использованию различных способов выполнения заданий. 6. Оценка (поощрение) при опросе на уроке не только правильного ответа ученика, но и анализ того, как ученик рассуждал, какой способ использовал, почему ошибся и в чём. 7. Обсуждение с детьми в конце урока не только того, что «мы узнали» (чем овладели), но и того, что понравилось (не понравилось) и почему, что бы хотелось выполнить еще раз, а что сделать по-другому. 8. Отметка, выставляемая ученику в конце урока, должна аргументироваться по ряду параметров: правильности, самостоятельности, оригинальности. 9. При задании на дом называется не только тема и объем задания, но и подробно разъясняется, как следует рационально организовать свою учебную работу при выполнении домашнего задания. На начальном этапе обучения я провожу диагностирование учащихся по таким параметрам как: уровень обученности, сформированность общеучебных умений и навыков , мотивы, характерологические особенности каждого ученика, уровень математических способностей. Для определения уровня актуальных знаний провожу контрольно-диагностический срез по предмету. Результаты диагностики помогают мне: составить характеристику личностного развития каждого учащегося ,выявить его тип мышления и проектировать его дальнейшее личностное развитие. Диагностика в целом способствует осуществлению личностно ориентированного подхода. Применение личностно ориентированных приемов обучения на различных этапах урока Этап актуализации субъектного опыта. Одним из способов является устный счёт. Формы его проведения различны: арифметическая головоломка, игра “Интеллектуальный марафон”, по программе, заданной блок-схемой, выполнить вычисления и расшифровать высказывание. Задания для устного счёта стараюсь брать занимательного характера, оформляю наглядно, красочно. Такие задания развивают воображение, внимание, память, мышление. Все задания содержат в себе элементы необычного, удивительного, вызывают интерес у школьников к предмету и способствуют положительной эмоциональной обстановке учения. Большое значение имеет организационный момент каждого урока.
Устные задания пи изучении темы «Некорорые свойства прямоугольных треугольников
Применение технологии проблемного обучения позволяет учителю перевести собственную деятельность из режима информирования в режим консультирования. Благодаря этой технологии центральное место в системе «учитель – ученик» занимает учащийся.. Проблемное обучение может быть использовано на различных этапах учебного процесса. В старших классах я применяю для актуализации знаний опережающую самостоятельную работу. Самостоятельная работа на опережающей основе пред полагает такое построение учебного процесса, при кото ром часть работы по теме предшествует совместному изучению нового учебного материала, выполняемая учащими самостоятельно. В основе метода лежат различные типы учебных и исследовательских заданий. Цель работы — вызвать у учащихся интерес к проблеме, которую предстоит изучать; овладеть какой-либо информа цией, которая поможет в изучении нового учебного материала, оценить его с позиций своего опыта. Опережающая самостоятельная работа способствует формиро ванию активности личности в учебном процесс, интенсифицирует и индивидуализирует учебный труд. Практика показала, что идея опережающей самостоятельной работы реализуется эффективнее, если соблюдается ряд условий: -задания берутся из дополнительных источников, а не по учебнику; -задания связаны с интересными проблемными задачами; -обучающиеся не наказываются за невыполненное задание, но поощряются за выполнение.
Проблема :Как найти гипотенузу прямоугольного
треугольника по двум известным катетам? Для решения этой проблемы проводим исследовательскую работу, предложив учащимся задание: построить прямоугольные треугольники с катетами 12 и 5; 6 и 8; 8 и 15 см и измерить гипотенузу. Предлагается выразить формулой зависимость между длинами катетов и гипотенузой в прямоугольных треугольниках. Школьники выдвигают свои гипотезы, которые обсуждаются Проверка гипотез : установление зависимости между сторонами прямоугольного треугольника Доказательство или опровержение гипотез :эмпирический вывод требует теоретического обоснования, доказывается теорема Пифагора (при изучении нового материала). Этап изучения нового материала. При изучении нового материала стараюсь максимально привлечь ребят поиском решения той или иной проблемы. Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Наиболее часто на уроках математики я использую технологии проблемного обучения при изучении нового материала. Учащиеся самостоятельно усваивают новое понятие, название которого вводится после усвоения его сущности. При разрешении проблемной ситуации учащиеся проходят все основные этапы этого процесса: анализ, выдвижение гипотезы, решение проблемы с использованием гипотезы, проверка правильности решения проблемы.
При изучении темы «Умножение дробей»(6 класс),можно провести небольшое исследование.
Примеры применения технологии проблемного обучения в моей практике Тема «Сумма n первых членов арифметической прогрессии» (изучение нового материала): ставлю проблему: В течение 30 секунд найдите сумму всех чисел на циферблате часов. Выслушав ответы учащихся, подвожу их к выдвижению гипотезы и выводу формулы. Тема «Неравенство треугольника»: предлагаю ученикам построить с помощью циркуля и линейки треугольник со сторонами: а) 5см; 6см; 7см; б) 1см; 2см; 3см. Ребята работают самостоятельно и приходят к тому, что построить треугольник в последнем случае не удается. Возникает проблема: «При каких же условиях существует треугольник»? Чертежи, полученные учащимися при решении этой задачи дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон». Доказываем полученную теорему. Этап применения знаний. Закрепление изученного материала практически всегда сопровождаю заданиями на составление обратной задачи. Такая форма работы применима к любой теме курса математики. Если учащиеся способны составлять обратную задачу, значит, они понимают смысл данного задания, видят взаимосвязь компонент.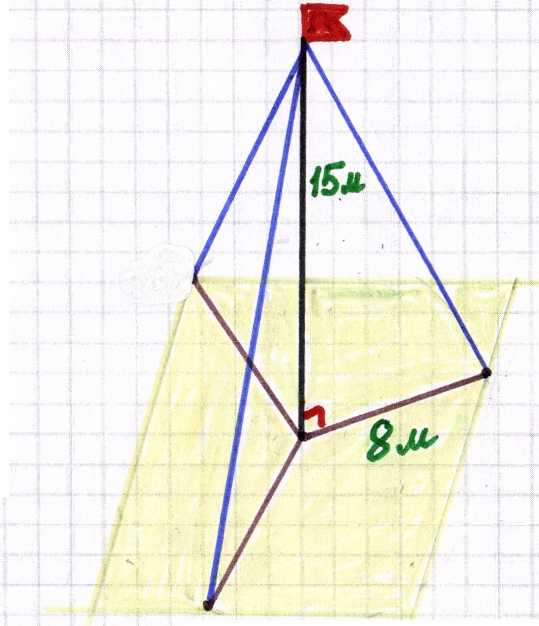 
Для закрепления математических понятий можно проводить дидактические игры Понятие «Вписанный четырехугольник» Задание. Если на вопрос учителя, считаете, что надо ответить «да», то поднимите руку, если «нет», то руку не поднимайте. Вопросы учителя. Является ли четырехугольник вписанным? : 1. Четырехугольник, у которого суммы противоположных сторон равны? 2. Четырехугольник, у которого сумма противоположных углов равна 1800? 3. Если это равнобедренная трапеция ? 4. .Если это ромб ?(возможны два ответа, комментирование учащихся»)
| |||||||||||||||||||||||||||||||||||||||||||||||
«Нахождение числа по его дроби»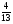
; 
; 
; .
; 
;
.
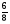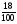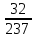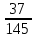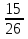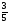; - 5; 
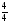; 3,5; -
; 
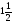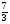;- 0,2; 
; 
;
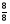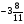