Тема «Преобразование графика квадратичной функции»

Скачать 49.44 Kb. Название Тема «Преобразование графика квадратичной функции» Дата 18.04.2016 Размер 49.44 Kb. Тип Урок

Тема «Преобразование графика квадратичной функции». иметь наглядные представления об основных свойствах квадратичной функции, иллюстрировать их с помощью графических изображений, уметь строить графики квадратичной функции, находить по графику промежутки возрастания и убывания, промежутки знакопостоянства, наибольшее и наименьшее значения. Цель урока: рассмотреть виды преобразований графика квадратичной функции. Задачи урока: Образовательные: • расширить сведения о свойствах квадратичной функции; •ознакомить учащихся с графиками частных видов квадратичной функции – функций у = ах2 , у = ах2 + n, y = a (x – m)2; у=a (x – m)2 +n. • научить строить и выполнять преобразования графиков квадратичной функции. Развивающие: развитие у учащихся аналитического мышления; развитие речи (расширение математического словаря). Воспитательные: привитие практических умений и навыков по построению графиков; воспитание познавательной активности; воспитание ответственности; воспитание культуры диалога. Тип урока: формирование новых знаний и умений. Оборудование: компьютер, мультимедийная презентация, доска и мел. Ход урока. 1. Организационный момент. 2. Актуализация знаний учащихся. 1.Проверка домашнего задания (разбор нерешенных задач, если они есть). 2.Контроль усвоения материала: Определение квадратичной функции; (слайд №2) Заполни пропуски…(слайд №3) Функция у=ах2+вх+с, где а, в, с – заданные действительные числа, а ≠0, х- действительная переменная, называется … функцией. (квадратичной) График функции у=ах2 при любом а≠0 называют… .( параболой). Функция у=ах2 является … (возрастающей, убывающей) на промежутке х ≤ 0. (убывающей). Значения х , при которых квадратичная функция равна нулю, называют… функции. (нулями функции) Точку пересечения параболы с осью симметрии называют… параболы. (вершиной параболы) При а>0 ветви параболы у=ах2 направлены… . (вверх) Если а< 0 и х ≠0, то функция у=ах2 принимает …(положительные, отрицательные ) значения. (отрицательные) 3. Изучение нового материала. (Работа в группах) 1).Построить графики функций в одной системе координат и сделать выводы об их расположении. 1 группа: у=х2, у=2х2, у= 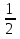х2. (слайд № 4,5) 2 группа: у=х2, у=х2+1, у=х2-1. (слайд № 6,7) 3 группа: у=х2, у=(х+1)2, у=(х-1)2. (слайд № 8,9) 2).Каждая группа представляет результаты работы и делает выводы. 3).Обобщение полученных сведений.(слайды № 10,11) f(x + n) n > 0 n < 0 Сдвиг влево вдоль оси ОХ на n единиц Сдвиг вправо вдоль оси ОХ на n единиц f(x ) + m m > 0 m < 0 Сдвиг вверх вдоль оси ОУ на m единиц Сдвиг вниз вдоль оси ОУ на m единиц f(x + n) + m n > 0, m > 0 n < 0, m < 0 Сдвиг влево вдоль оси ОХ на n единиц, затем сдвиг вверх вдоль оси ОУ на m единиц Сдвиг вправо вдоль оси ОХ на n единиц, затем сдвиг вниз вдоль оси ОУ на m единиц n > 0, m < 0 n < 0, m > 0 Сдвиг влево вдоль оси ОХ на n единиц, затем сдвиг вниз вдоль оси ОУ на m единиц Сдвиг вправо вдоль оси ОХ на n единиц, затем сдвиг вверх вдоль оси ОУ на m единиц 4.Закрепление полученных знаний. (слайд№ 12) 1) График какой функции, изображенной на рисунках соответствует указанной формуле у=3х2+1. (слайд№ 13) 2) График какой функции, изображенной на рисунках соответствует указанной формуле у= -0,5х2-3. (слайд№ 14) 3) График какой функции, изображенной на рисунках соответствует указанной формуле у= -2(х-2)2 .(слайд№ 15) 4).График какой функции изображенной, на рисунках соответствует указанной формуле у= (х+2)2 – 4. (слайд№ 16) 5).Какой формулой задается график функции, изображенной на рисунке: у = (х+2)2 – 2, у = 2 - (х+2)2, у = 2+ (х+2)2, у = (х+2)2. (слайд№ 17) 6).Какой формулой задается график функции, изображенной на рисунке: у = 2(х+3)2 +4, у = 2(х-4)2 -3, у = 3-2 (х+4)2, у = -2(х-3)2 +4 (слайд№ 18) Вывод. В заданиях 4), 5), 6) выполняются два преобразования графика функции: сдвиг вдоль осей Ох и Оу. 5.Итоги урока. Виды преобразований и способы построения графиков квадратичной функции. 6.Рефлексия. (слайд№ 19) Лист рефлексии Подчеркните, пожалуйста, те состояния, которые Вы испытывали в процессе сегодняшнего урока: интерес беспокойство эмоциональный подъем скука удовольствие раздражение 7.Домашнее задание. (слайд№ 20) 1.Построить в одной системе координат графики функций: а) у=1/2х2 ; б) у=-1/2(х-3)2 ; в) у=1/2(х+3)2-2. 2. Укажите координаты вершины параболы и направление ветвей: а)y = -3x2+5; б)y = (x+5)2+2; в)y = -0,5(x-2)2+3; г)y = 2(x-3)2.