|
Преподаватель: Рогожкина Ольга Юрьевна

Преподаватель: Рогожкина Ольга Юрьевна
Интеграция – сторона процесса развития, связанная с объединением в целое ранее разнородных частей и элементов. Основой для интеграции является теория межпредметных связей.

Так, А. В. Усова рассматривает межпредметные связи как дидактическое условие повышения научного уровня знаний, развития мышления и творческих способностей, оптимизации учебного процесса. В. Н. Максимова относит межпредметные связи к одному из принципов обучения.

И. Д. Зверев проблему межпредметных связей выводит из дидактического принципа системности. И. Д. Зверев проблему межпредметных связей выводит из дидактического принципа системности. “Межпредметные связи предполагают взаимную согласованность содержания образования по различным учебным предметам, построение и отбор материала, которое определено общими целями образования, а также оптимальным учетом познавательных задач, обусловленных спецификой каждого учебного предмета”.

Содержательно-информационные связи - связи на основе содержания знаний. Содержательно-информационные связи - связи на основе содержания знаний.2. Операционно-деятельностные связи - связи на основе учебно-познавательной деятельности и умений учащихся в обучении.
3. Организационно-методические связи - связи на основе тех или иных методов и организационных форм.

Сетевое планирование, Сетевое планирование, курсовое планирование, поурочное планирование.

Использование межпредметных связей - одна из наиболее сложных методических задач учителя математики. Использование межпредметных связей - одна из наиболее сложных методических задач учителя математики. Она требует знаний содержания программ и учебников по другим предметам.

Информатика – это благодатная почва для межпредметных связей с другими предметами. Информатика – это благодатная почва для межпредметных связей с другими предметами. Совмещая изучение разных предметов и информатики одновременно снижается нагрузка на учащихся, используются более эффективные способы обучения. Выявлены межпредметные связи информатики со всеми учебными предметами.


Тема: «Дифференциальное исчисление. Физическое приложение производной». Тема: «Дифференциальное исчисление. Физическое приложение производной».Зависимость пути от времени при прямолинейном движении точки задана уравнением S=1/3t3+2t2-3. Вычислить ее скорость в момент времени 4с.Скорость точки, движущейся прямолинейно, задана уравнением V=2t2-5t+6.+ В какой момент времени ускорение точки будет равно 2м/с2.

Тема: «Интегральное исчисление. Неопределенный интеграл, определенный интеграл». Тема: «Интегральное исчисление. Неопределенный интеграл, определенный интеграл».Скорость точки, движущейся прямолинейно, задана уравнением V=t2-4t+3. Найти закон движения точки, если за время 3с она пройдет путь 20 м.Какую работу нужно совершить, чтобы растянуть пружину на 10 см, если сила в 20 Н растягивает пружину на 5 см?

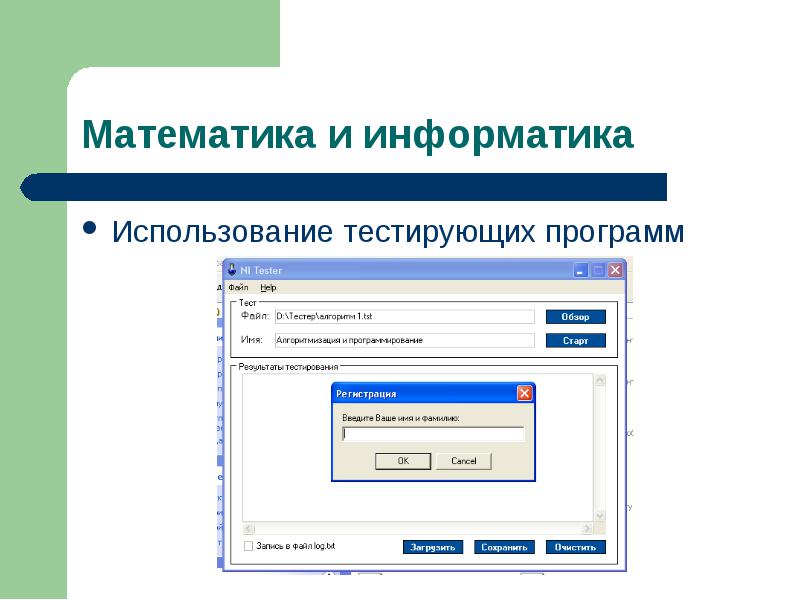
Использование тестирующих программ Использование тестирующих программ
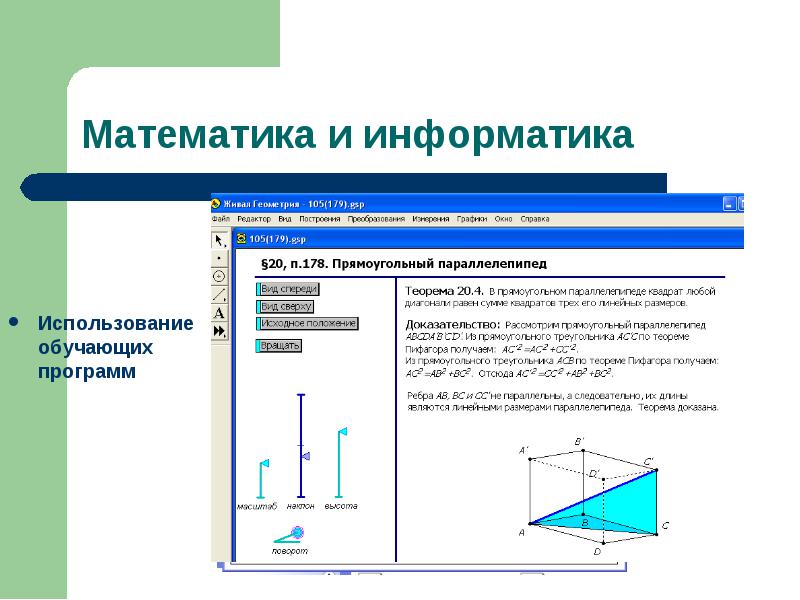
Использование обучающих программ Использование обучающих программ
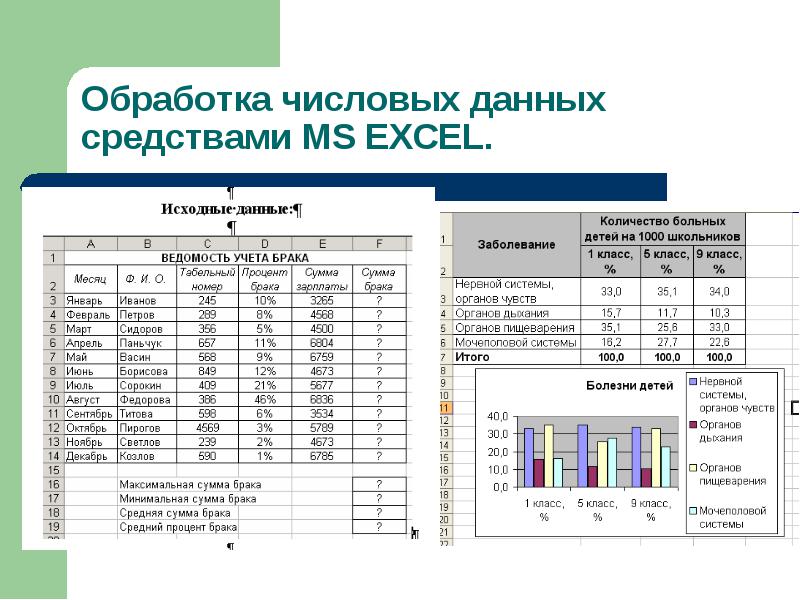
При изучении раздела «Линейная алгебра» следует изучить ряд математических функций мастера функций fx пакета MS Excel При изучении раздела «Линейная алгебра» следует изучить ряд математических функций мастера функций fx пакета MS Excel




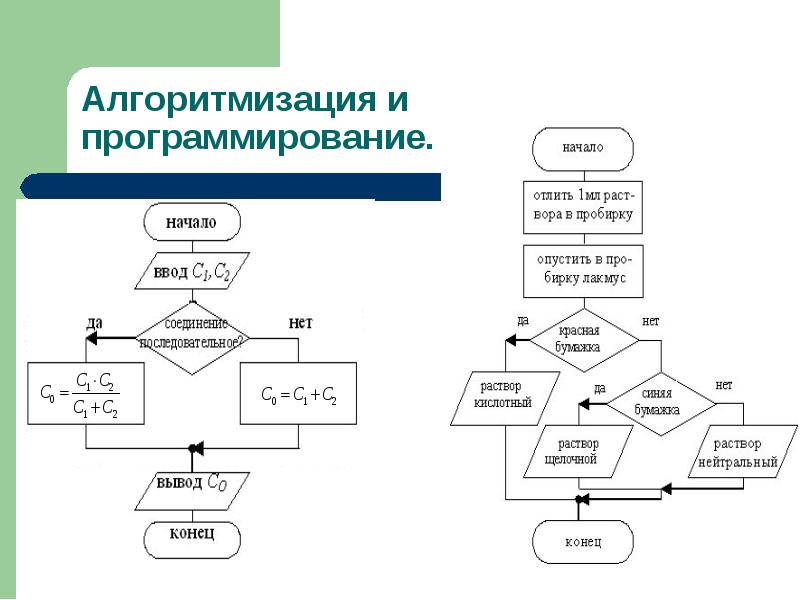
Каждая бактерия делится на две через 1 мин. В начальный момент имеется 1 бактерия. Сколько бактерий будет через N мин? Каждая бактерия делится на две через 1 мин. В начальный момент имеется 1 бактерия. Сколько бактерий будет через N мин?Программа подсчета количества бактерий.- 10 CLS
- 20 Input "Введите количество минут";n
- 30 For i=1 to n
- 40 k=2^i
- 50 Next i
- 60 Print "Количество бактерий=";k
- 70 End


Габидуллина Л. Л., Сырцова Е. Л. Межпредметная интеграция как условие развития познавательной активности младших школьников. - Ярославский педагогический вестник. 2003. № 2 (35) Габидуллина Л. Л., Сырцова Е. Л. Межпредметная интеграция как условие развития познавательной активности младших школьников. - Ярославский педагогический вестник. 2003. № 2 (35) URL: https://vestnik.yspu.org/releases/pedagoka_i_psichologiy/20_3/Максимова В.Н., Зверев И.Д. Межпредметные связи в учебно-воспитательном процессе в современной школе. М.: Просвещение, 1987. 180 с. Межпредметные связи естественно-математических дисциплин. Пособие для учителей. Сб. статей/Под ред. В. Н. Федоровой. - М., Просвещение, 1980. – 208с., ил.

 |
|
|
 Скачать 445 b.
Скачать 445 b.






















