Рабочая программа курса по выбору по математике «избранные вопросы геометрии» для учащихся 9 класса

Скачать 213.48 Kb. Название Рабочая программа курса по выбору по математике «избранные вопросы геометрии» для учащихся 9 класса Дата 18.04.2016 Размер 213.48 Kb. Тип Рабочая программа

Муниципальное казенное общеобразовательное учреждение «Ишимская основная общеобразовательная школа» Утверждена Приказом №_____от «___»_________2015г. Директор ______Л. В. Антонова РАБОЧАЯ ПРОГРАММА КУРСА ПО ВЫБОРУ ПО МАТЕМАТИКЕ «ИЗБРАННЫЕ ВОПРОСЫ ГЕОМЕТРИИ» для учащихся 9 класса Количество часов -17 часов Количество часов в неделю- 0,5 часа Составитель: Некрасова А. М., учитель математики Принята на заседании РМО Протокол № _________ от «___» __________2015г Руководитель РМО ______ Принята педагогическим советом Протокол № __________ от «___» ___________2015г с. Ишим 2015 Содержание: Пояснительная записка …………………………………………………………………….. 3 Календарно-тематическое планирование...………..……………………………………….5 Содержание программы …………………………………………………………………….6 Список литературы …................ ……………………………………………………………. Приложения……………. …………………………………………………………………… Пояснительная записка Содержание курса имеет определенное отличие от базового курса математики, которое состоит в том, что такой раздел геометрии как «Метрические соотношения в треугольнике» представлен односторонне, не отражены другие точки зрения на доказательство теоремы Пифагора и ее обобщений, а об общекультурном аспекте упоминается вскользь. Мало задач на практическое применение, не рассматриваются решения задач имеющих широкий круг применения в курсах смежных дисциплин. Элективный курс «Избранные вопросы геометрии: обобщения и применения теоремы Пифагора» направлен на углубление и расширение тем «Теорема Пифагора» и «Обобщенная теорема Пифагора», на формирование общекультурной компетентности, создание представлений о математике как науке, возникшей из потребностей человеческой практики и развивающейся из них, а также собственных внутренних закономерностей. Данный элективный курс поможет учащимся познакомятся с любопытными геометрическими и историческими фактами, оригинальными подходами к доказательству и применению теоремы Пифагора, с решением задач имеющих широкий круг применения в курсах смежных дисциплин и практической деятельности человека. Курс характеризуется рациональным сочетанием логической строгости и геометрической наглядности. Теоретический материал сопровождается: разбором задач, приведены упражнения для самостоятельной работы, вопросы самопроверки, задания для практической работы в среде «Живая геометрия»1, темы творческих работ для самостоятельной работы учащихся. Учащиеся овладевают приемами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Постоянное обращение к наглядности, использование чертежей развивает геометрическую интуицию. Наряду с основной задачей обучения математике - обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, выбор профиля дальнейшего обучения. Цели курса: помочь повысить уровень понимания и практической подготовки в таких вопросах, как решение геометрических задач; помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы, показать возможности применения полученных знаний в своей будущей профессии; создать в совокупности с основными разделами курса базы для развития способностей учащихся; Задачи курса: Убедить в практической необходимости применения геометрического аппарата к решению задач; расширить представления учащихся о сферах применения геометрии (не только в естественных науках, но и в технике, производстве, в гуманитарной сфере) помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования; помочь ученику оценить свой потенциал с точки зрения образовательной перспективы. Данный курс рассчитан на 17 часов, предполагает компактное и четкое изложение теории вопроса, решение задач, самостоятельную работу. Предпочтительны такие формы проведения занятий, как: Лекция-беседа Лекция с мультимедиа демонстрациями Семинар Практическая работа в среде «Живая геометрия» Итоговая конференция с выставкой творческих работ учащихся. В состав учебно-методического комплекта входят: 1. Учебное пособие для школьников, включающее задачи и упражнения для закрепления знаний и отработки практических навыков, упражнения для самостоятельной работы, тесты, темы творческих работ для самостоятельной работы учащихся. 2. Методическое пособие для учителя с методическими рекомендациями по проведению занятий, решению задач, организации промежуточного и итогового контроля знаний учащихся. 3. Приложения, содержащие дополнительную информацию по данному курсу. Календарно-тематическое планирование № п/п Наименование тем курса Всего часов В том числе Дата лекция практика I. Теорема Пифагора. Различные способы доказательства теоремы Пифагора Доказательства теоремы Пифагора, основанные на понятии площади. Алгебраический метод доказательства теоремы Пифагора. 4 2 2 1 1 1 1 II. Применения теоремы Пифагора. 3. Обратная теорема Пифагора. Пифагоровы числа. 4. Формула Герона. 5.Решение задач на применение теоремы Пифагора 5 2 1 2 1 1 1 1 1 III. Обобщения теоремы Пифагора 6.Теорема Пифагора, доказанная Евклидом. Теорема косинусов. 7.Доказательство теоремы Пифагора через отношение подобных фигур. 8.Стереометрические обобщения теоремы Пифагора для тетраэдров и трехгранных углов. 6 2 2 2 1 1 1 1 1 1 IY. Итоговое занятие 2 2 Содержание программы Тема 1. Теорема Пифагора. Различные способы доказательства теоремы Пифагора (4 ч.) Предмет, изучению которого посвящен данный курс. Историческая справка. Доказательства теоремы Пифагора, основанные на понятии площади. Алгебраические доказательства. Занятие 1, 2. Введение. Доказательства теоремы Пифагора, основанные на понятии площади. (2ч). Доказательство теоремы Пифагора, основанные на использовании равновеликости фигур, аддитивные доказательства, доказательство методом разложения квадратов на равные части; доказательство методом достроения. Методы обучения: лекция-беседа с использованием приема активного слушания; практическая работа в «Живой геометрии», обсуждение тем сообщений и рефератов; исследовательский метод обучения, обеспечивающий творческое применение знаний. Формы контроля: проверка задач самостоятельного решения, творческих заданий. Занятие 3, 4. Алгебраический метод доказательства теоремы Пифагора. (2ч) Методы обучения: лекция, учебная беседа с использованием приема активного слушания; обсуждение тем сообщений и рефератов; выступления, практическая работа в «Живой геометрии», проектирование собственных задач. Формы контроля: Выступление учащихся с докладами, проверка рефератов, творческих заданий. Тема 2. Применения теоремы Пифагора (5 ч.) Обратная теорема Пифагора. Пифагоровы числа. Формула Герона. Решение задач. Занятие 5, 6. Обратная теорема Пифагора. Пифагоровы числа. Решение задач (2 ч). Методы обучения: объяснение, выполнение тренировочных упражнений, обсуждение тем сообщений и рефератов; выступления, Формы контроля: Защита проектов решений задач, самостоятельная работа. Занятие 7. Формула Герона.(1 ч) Вывод формулы Герона разными способами. Формула Герона для иррациональных чисел. Решение задач на применение формулы Герона. Методы обучения: семинар, работа в группах, обсуждение тем сообщений и рефератов; выступления, выполнение тренировочных упражнений. Формы контроля: проверка рефератов, докладов, проекты решения задач, проверка задач самостоятельного решения. Занятие 8, 9. Решение задач на применение теоремы Пифагора при геометрических вычислениях; в смежных предметах; в практической деятельности человека. (2 ч). Методы обучения: объяснение, беседа с активным участием учащихся; проектирование собственных задач, выполнение тренировочных упражнений. Формы контроля: проверка задач самостоятельного решения, проекты решений задач. Тема 3. Обобщения теоремы Пифагора. (6 ч) Теорема Пифагора, доказанная Евклидом в «Началах». Обобщение теоремы Пифагора на случай произвольного треугольника (теорема косинусов). Доказательство теоремы Пифагора через отношение площадей подобных фигур. Луночки Гиппократа. Обобщение теоремы Пифагора на случай произвольного треугольника, на двух сторонах которого построены параллелограммы (Теорема Паппа). Стереометрические обобщения теоремы Пифагора для тетраэдров и трехгранных углов. Занятие 10, 11. Теорема Пифагора, доказанная Евклидом в «Началах», обобщение теоремы Пифагора на случай произвольного треугольника (теорема косинусов). Применение теоремы косинусов для решения задач. (2 ч). Методы обучения: Лекция с мультимедиа демонстрациями объяснение, выполнение тренировочных упражнений, практическая работа в «Живой геометрии». Формы контроля: самостоятельная работа, самоконтроль. Занятие 12, 13. Доказательство теоремы Пифагора через отношение площадей подобных фигур.(2 ч) Рассматриваются доказательства теоремы Пифагора через отношение площадей подобных фигур. Луночки Гиппократа. Обобщение теоремы Пифагора на случай произвольного треугольника, на двух сторонах которого построены параллелограммы (Теорема Паппа). Методы обучения: Лекция с мультимедиа демонстрациями, объяснение, выполнение тренировочных упражнений, практическая работа в «Живой геометрии». Формы контроля: проверка задач самостоятельного решения, творческих заданий. Занятие 14, 15. Стереометрические обобщения теоремы Пифагора для тетраэдров и трехгранных углов. Решение задач. (2 ч). Методы обучения: лекция-беседа, выполнение тренировочных упражнений. Формы контроля: проверка задач самостоятельного решения. Занятие 16, 17. Подведение итогов. (2 ч). Формы контроля: Защита проектов, творческих работ. Список литературы Атанасян Л.С.,и др. Геометрия 7-9. - М.: Просвещение, 2004 Атанасян Л.С,и др. Методические рекомендации к учебнику геометрии в 7, 8, 9 классах: Кн. Для учителя - М.: Просвещение, 2004 Гаврилова Н.Ф. Поурочные разработки по геометрии/в помощь школьному учителю/, дифференцированный подход, 8 класс. – М.: «ВАСКО»,2006 Глейзер Г.И. История математики в школе. - М.:Просвещение,1964 Еленьский Ш. По следам Пифагора.- М.: Просвещение , 1960 Люберанский А.И. Что можно узнать из формулы Герона?. – Школа-Пресс.: Журнал Математика в школе № 6, 1998. Зив Б.Г. Задачи к урокам геометрии,7-11,- С.-Петербург.: НПО Мир и семья,1996 Скопец З.А. Геометрические миниатюры.- М.:Просвещение ,1990 Все о 120 стандартах перспективных работ на рынке труда: Журналы Завуч: № 3, №6, №8- 2000г, №1, №2 -2001г. № ЭОР Аннотация 1 https://th-pif.narod.ru/ На этом сайте вы сможете найти сведения об истории открытия и доказательства теоремы Пифагора, а так же о самом Пифагоре. Здесь приведены около 30 различных доказательств этой теоремы от древнейндийского математика Басхары до векторного доказательства. Вы сможете узнать, как использовали свойства и теорему прямоугольного треугольника древние египтяне, архитекторы средневековья и как она используется в наше время 2 https://ru.wikipedia.org/wiki/ Теорема_Пифагора Материал из Википедии — свободной энциклопедии Сайт о теореме Пифагора с большим числом доказательств материал взят из книги В.Литцмана, большое число интерактивных чертежей. 3 https://exponenta.ru/educat/ systemat/masterov/index.asp Обобщенная теорема Пифагора-теорема косинусов. сайт математика-любителя Мастерова А.В. " теорему косинусов школьникам нужно преподносить именно как обобщение теоремы Пифагора. Это позволит учащимся перенести практический опыт использования теоремы Пифагора на теорему Косинусов".   4 https://schools.keldysh.ru/sch119/Project/2005-2006/9/Mesropian/0201.htm Проект по геометрии: «Пифагор. Теорема Пифагора». Автор: Месропян Арамаис, ученик 9 класса .Цель создания этого проекта – возможность собрать и представить наиболее полную информацию по данной теме для того, чтобы дать возможность другим ученикам получить более глубокие сведения по теме «Теорема Пифагора» На сайте расположены флеш-лекции "Прямая и обратная теорема Пифагора" и "Теорема Пифагора и бильярд" 5 https://alleng.ru/d/math/math235.htm Эта небольшая книжка, написанная известным немецким популяризатором математики, профессором Гёттингенского университета Вальтером Литцманом, посвящена не только геометрии, как можно было бы подумать по её названию. Автор собрал в ней довольно разнообразный материал, относящийся и к геометрии, и к алгебре, и к арифметике. Весь этот материал группируется вокруг знаменитой ТЕОРЕМЫ ПИФАГОРА   6 https://geometr.info/geometriia/arhiv.html тесты ,решение задач на применение теоремы Пифагора Приложение № 1 Банк заданий для использования на занятиях элективного курса. Тема 1. Теорема Пифагора. Различные способы доказательства теоремы Пифагора Вопросы для устной работы: В чем заключается теорема Пифагора? Какое ей можно дать истолкование, используя понятие площади? Что вы знаете о Пифагоре? Знаете ли вы другие доказательства теоремы Пифагора? Задания для самостоятельной работы учащихся. Поручить нескольким учащимся подготовить выступления-содоклады к лекции учителя (Различные способы доказательства теоремы Пифагора) Практическая работа в среде «Живая геометрия» (интерактивные чертежи) «Смотри!»-Ответить на вопросы и объяснить доказательства: Какая теорема доказана и как? Объясните алгебраическое доказательство? «Доказательство Леонардо»-Попробуйте восстановить доказательство; «Шарнирное доказательство»- Дайте полное доказательство. «Пифагоров паркет»-Восстановите доказательство по рисунку, построение нарушается когда зеленый квадрат становится большим, но все равно рисунок дает доказательство для всех возможных случаев .Почему?; «Теорема Пифагора и квадрат суммы»-Восстановите заключенное здесь доказательство теоремы Пифагора. Попутно здесь выводится формула квадрата суммы. Как?; «теорема Пифагора по Евклиду»-Докажите, что при всех преобразованиях треугольника его площадь не меняется. Объясните, как отсюда выводится теорема Пифагора? Творческое задание: самостоятельное открытие доказательства теоремы Пифагора. Для учащихся, которым это задание окажется сложным предлагается доказать теорему по рисункам иллюстрирующих 8 способов на которые имеются ссылки в «Началах». Написать рефераты по темам: «Пифагор, философ, математик», «Магический квадрат Пифагора», «Пифагор и его союз», «Философские начала пифагорейцев», «Значение пифагореизма», т.п.. Тема для дискуссии: Какое из доказательств теоремы лучше и почему? (Учащиеся отстаивают свою точку зрения. Критикуют другие способы доказательства.) Тема 2. Применения теоремы Пифагора. Задания для самостоятельной работы учащихся. 1.Вопросы: Для каких треугольников она применяется? Какие задачи позволяет решать теорема Пифагора? Какие данные надо иметь в прямоугольном треугольнике и какие действия с ними произвести, чтобы найдите по теореме Пифагора: а) гипотенузу?; б) катет? Гипотенуза и катеты прямоугольного треугольника обозначены соответственно с, а, в. Площадь каких фигур выражают: с2 , а2 ,в2 ? Сформулируйте теорему Пифагора, используя понятие площади квадрата. Какие треугольники называют Пифагоровыми? Что можно сказать о сравнительной длине: а) гипотенузы и катета; б) наклонной к прямой, проведенных из одной точки, и их проекций? 2. Задачи на применение прямой и обратной теоремы Пифагора (задачи располагаются по нарастающей трудности): Задача № 1: В параллелограмме АВСD ВD =241 см, АС = 26 см, АD = 16 см. Через точку О – точку пересечения диагоналей параллелограмма проведена прямая, перпендикулярная стороне ВС. Найдите отрезки, на которые эта прямая разделила сторону АD. Ответ: 4 см;.9 см. Задача № 2: В треугольнике АВС АВ = ВС . Высота АК делит сторону ВС на отрезки ВК = 24 см и КС = 1 см. Найдите площадь треугольника и сторону АС. Ответ: АС=5 2 см; S= 87,5 см2 Задача № 3: Две окружности радиусами 13 и 15 см пересекаются. Расстояние между их центрами О1 и О2 равно 14 см. Общая хорда этих окружностей АВ пересекает отрезок О1О2 в точке К. Найдите О1К и КО2 ( О1 –центр окружности радиусом 13 см). Ответ: О1К=5см, КО2=9 см. Задача №4: В треугольнике АВС АВ = АС. Высота ВМ равна 9 см и делит сторону АС на два отрезка так, что АМ = 12 см. Найдите площадь и периметр треугольника. Ответ: Р=30 + 3 10 см., S = 67,5 см2 Задача № 5: На стороне АD параллелограмма АВСD взята точка Е так, что АЕ = 4 см, ЕD = 5 см, ВЕ = 12 см, ВD = 13 см. Найдите площадь параллелограмма. Ответ:108 см2 Задача № 6: В остроугольном треугольнике АВС проведены высоты АК и СЕ, СЕ = 12 см, ВЕ = 9 см, АК = 10 см. Найдите АС. Ответ:АС=12,5 см. Задача № 7: В равнобедренной трапеции АВСD АD║ВС,<А = 300, высота ВК = 1 см, ВС = 2 3 см. Найдите площадь треугольника КМD, если М – середина отрезка ВD. Ответ: 3 3 / 4 см2 Задача № 8*: В выпуклом четырехугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырехугольник является параллелограммом. Задача № 9*: В выпуклом четырехугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD и АСD равны, а площади треугольников АСD и ВСD не равны. Докажите, что данный четырехугольник является трапецией. Задача № 10. Где ошибка? «Новое доказательство» теоремы Пифагора. Возьмем прямоугольный треугольник с катетами а и b, гипотенузой с и острым углом , противолежащим катету а. Имеем: а =csin, b=ccos, откуда а2 = с2sin2 b2=c2cos2. Просуммировав по частям эти равенства, получаем: а 2 + Ь 2=с 2 (sin2 +cos2). Но sin2 +cos2 = 1, и поэтому а 2 + Ь 2=с 2 Подвергните критике это -доказательство». Ответ: формула sin2 +cos2 = 1 выводится на основании теоремы Пифагора, и поэтому в рассуждении получается порочный круг. Пифагоровы числа Темы докладов по теме Пифагоровы числа Пифагорейское учение о числе. Пифагоровы числа и их свойства. Тема для сочинения: «Магический квадрат Пифагора» Задача: Докажите, что катеты а, в и гипотенуза с таких треугольников выражаются формулами: а = 2тп, в = т2 - п2, с = т2 + п2, где т и п — любые натуральные числа, такие, что т > п. Темы для докладов к теме формула Герона: Историческая справка о Героне Александрийском. Выводы формулы Герона разными способами. Преобразование формулы Герона, для работы с иррациональными числами. задачи, на применение формулы Герона. Тема для дискуссии: Какой вывод формулы Герона лучше? (каждый из участников защищает «свой» способ и критикует «чужой») Задачи на применение формулы Герона: 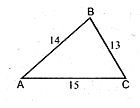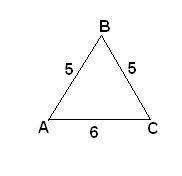Задача № 1:Найти SABC; Задача № 2:Найдите площадь четырехугольника ABCD , в котором АВ=5 см, ВС=13 см, CD=9см, DA=15 см, АС=12см. Ответ:84 см2 Задача № 3:Расстояние от точки М, лежащей внутри треугольника АВС, до прямой АВ равно 6 см, а до прямой АС равно 2 см. Найдите расстояние от точки М до прямой ВС, если АВ =13см, ВС = 14 см, АС = 15 см. Ответ:4 см. Задача №4:Вычислите площадь треугольника, если длины сторон 2; 37; 17. Исследовать: Задача № 5: Какую форму нужно придать треугольнику, чтобы при данной сумме его сторон он имел наибольшую площадь? Ответ: Треугольник имеет при данном периметре наибольшую площадь тогда, когда стороны равны между собой. (равносторонний треугольник) Применение теоремы Пифагора при изучении смежных дисциплин и практической деятельности человека. Задача № 1:С аэродрома вылетели одновременно два самолёта: один - на запад, другой - на юг. Через два часа расстояние между ними было 2000 км. Найдите скорости самолётов, если скорость одного составляла 75% скорости другого. Ответ: 800 км/ч.; 600 км/ч. Задача № 2:Как следовало бы поступить юному математику, чтобы надёжным образом получить прямой угол? Ответ: Проще всего взять для этого планки длиной в 3, 4 и 5 каких-либо произвольно выбранных равных отрезков. Задача №3:Найдите равнодействующую трёх сил по 200 Н каждая, если угол между первой и второй силами и между второй и третьей силами равен 60°. Ответ: R=400 Н. Задача № 4:Молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. Ответ: h≥(a2+b2)1/2 Задача № 5:Какую наибольшую высоту должна иметь телевизионная вышка, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.) Ответ: 2,3 км. Задача № 6:При измерительных работах в полеводстве широко используется так называемая сажень (полевой циркуль) – инструмент в виде буквы А высотой 1,37 м ишириной 2 м.Какой длины заготовки требуются для изготовления сажени? Ответ: Задача № 7:Телевизионные радиосигналы распространяются на 15 % дальше пределов прямой видимости антенны. При каком наибольшем расстоянии S от передающей антенны высотой H можно принять телепередачу с помощью приемной антенны высотой h ? Определите, при каком максимальном расстоянии можно принять передачу с помощью антенны высотой 20 м с Останкинской башни (её высота 538 м). Ответ: S= 4,1 . 103(  H +  h)м. Задача № 8:Выпрямление окружности. .Если нужно выпрямить окружность О радиуса r то проводят диаметр АВ, а в точке В – перпендикулярную к ней прямую СД. Из центра о под углом 30 к АВ проводят прямую ОС. Затем на прямой СД от точки С откладывают три радиуса данной длиной окружности и соединяют полученную точку Д с А: длина отрезка АД равна длине полуокружности. Если отрезок АД удлинить вдвое, то приближенно получится выпрямленная окружность О, ошибка менее 0,0002r. На чем основано это построение? Ответ:3,14153 r. Тема 3. Обобщения теоремы Пифагора. Задания для самостоятельной работы учащихся. Вопросы: 1.В чем заключается обобщенная теорема Пифагора? 2.Докажите ОТП. 3.Почему ОТП имеет такое название? 4.Какие задачи по решению треугольников вы можете решить с помощью ОТП? 5.Как определить вид углов треугольника с помощью ОТП? 6.Какие практические задачи вы можете решить с помощью ОТП? 1.Практическая работа в среде «Живая геометрия» (интерактивные чертежи) «Теорема косинусов без косинусов. Рассуждения Евклида»-Покажите тем или иным способом, что розовые прямоугольники равновелики и выведите утверждение Евклида. Как их него получается теорема косинусов? «теорема Паппа»-восстановите доказательство. Творческое задание: самостоятельно доказать теорему через отношение площадей подобных фигур предварительно выбрав правильную фигуру. Например:«Площадь правильного треугольника, построенного на гипотенузе, равна сумме площадей правильных треугольников, построенных на катетах». Задачи: Задача № 1.Дан куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании. Найдите диагональ d? Ответ: d=√ 3*a Задача № 2 .Исследуем пирамиду, например, такую в основании которой лежит квадрат, и высота которой проходит через центр квадрата. Пусть сторона квадрата a, а высота пирамиды h. Чему равна длина S боковых рёбер пирамиды? Ответ: S2=h2+1/2*a2. Задача № 3 Докажите, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений. Ответ: d2 = AB2 = AC2 + CB2 = (AD2 + DC2) + CB2 = a2 + b2 + c2. Задача № 4 Найди ошибку! а2= b2+ c2+2bc cos.; b2= а2+ c2-2bc cos; а2= а2+ c2 -2ac sin; ++=900; AB2=AC2+BC2-2 sin Задача № 5 Найди ошибку! Задача № 6 Определить вид треугольника со сторонами 5, 6 и 7 см. Выбрать и подчеркнуть верный ответ а) остроугольный' б) равнобедренный; в) тупоугольный; г) прямоугольный. Ответ: а) Задача № 7 В треугольнике АВС угол А равен 120°, АВ=АС=2 см. Найти длину стороны ВС. Выбрать и подчеркнуть верный ответ: Ответ: в) Задача № 8 В параллелограмме острый угол равен 60°Н а стороны 6 см н 8 см. Найти меньшую диагональ. (3 балла) Выбрать и подчеркнуть верный ответ: Ответ: б) Задача № 9: Угол при основании равнобедренного треугольника 30°, а боковая сторона равна 14 см. Найти медиану, проведенную к боковой стороне. . (4 балла) Выбрать и подчеркнуть верный ответ: Ответ: в) Задача № 10: Найти углы треугольника, если а=12, Ь=8; с=10. .(6 баллов) Верный ответ:  = 82049’;  = 410 24’;  = 550 47’. Задача № 11:Найти диагональ ВD параллелограмма АВСD, если она в 2 раза меньше стороны АВ угол АBD равен 60", АC=34 см. .(5 баллов) Верный ответ: 34 / 15 см. Задача № 12:В ромбе со стороной 10 см высота, опущенная из вершины тупого угла, делит сторону ромба на отрезки 3 см и 7 см. Найти меньшую диагональ ромба. .(5 баллов) Верный ответ: 2 15 см. Задача № 13: У треугольника длины сторон, а=6, b=8 и площадь S= 315. Третья его сторона меньше удвоенной медианы, проведенной к ней. Найти радиус вписанной в этот треугольник окружности. Ответ: r= 15/3 В конце изучения курса проводится анкетирование, позволяющее учащимся осознать, чем завершился для них данный курс. Что узнал о себе, изучая курс? Что изменил бы в курсе? Какие формы учебных занятий понравились больше всего? 1