Рабочая учебная программа по алгебре для 9 класса на 2013-2014 учебный год Составила: Овчинникова О. Н. учитель математики

Скачать 373.44 Kb. Название Рабочая учебная программа по алгебре для 9 класса на 2013-2014 учебный год Составила: Овчинникова О. Н. учитель математики Г.М.Кузнецовой Дата 11.04.2016 Размер 373.44 Kb. Тип Рабочая учебная программа

МОУ СОШ пгт Новокручининский Рабочая учебная программа по алгебре для 9 класса на 2013-2014 учебный год Составила: Овчинникова О.Н. учитель математики пгт Новокручининский 2013г.  Пояснительная записка Рабочая учебная программа составлена на основе авторской программы Г.М.Кузнецовой для образовательных учреждений. Программа ориентирована на УМК А.Г. Мордкович «Алгебра 9. - М.:Мнемозина 2010 г.), с учетом примерной программы основного общего образования по математике, утвержденной Министерством образования и науки РФ для образовательных учреждений Российской Федерации, реализующих программы общего образования, в соответствии с требованиями федерального государственного стандарта основного общего образования. Рабочая программа рассчитана на 102 учебных часа из расчёта 3 учебных часа в неделю. На проведение контрольных работ отводится  7 часов. Данная рабочая программа полностью отражает базовый уровень подготовки школьников по разделам программы. Она конкретизирует содержание тем образовательного стандарта и дает распределение учебных часов по разделам курса. При составлении программы учитывались особенности образовательного учреждения, которое реализует программу «Современные методы и организационные формы обучения предмету, обеспечивающие новое качество знаний» и особенности класса. 9 класс в своем составе имеет учащихся с различным уровнем обученности. Часть из них усваивает знания на уровне функциональной грамотности: К.Д, К.Э.,К.Д., для этих учащихся нужно всегда готовить дополнительные задания прикладного, исследовательского, проблемного характера, нестандартные и олимпиадные задачи. На уровне элементарной грамотности усваивают знания следующие учащиеся: Д.К.,В.П., этим учащимся нужно периодически оказывать помощь. Гораздо сложнее усваивают материал: К.Н., С.В., С.К., Б.В., Г.А., ,Л.В., М.С., М.С., М.С., С.Д., С.В. им необходима постоянная помощь со стороны учителя: индивидуально повторить новый материал, помочь при выполнении самостоятельной работы. В рамках отведенных часов необходимо выделить часы для тренировочных и диагностических работ, поэтому многие темы претерпевают изменения. Общая характеристика учебного предмета Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. Одной из главных особенностей курса алгебры является то, что в нем реализуется взаимосвязь принципов научности и доступности и уделяется особое внимание обеспечению прочного усвоения основ математических знаний всеми учащимися. Особенностью курса является также его практическая направленность, которая служит стимулом развития у учащихся интереса к алгебре, а также основной для формирования осознанных математических навыков и умений. «Идеология» основного курса алгебры делает его органическим продолжением и обобщением курса арифметики. Центральное понятие этого курса – понятие числа – развивается и расширяется от рационального до действительного. Усвоение алгебры осуществляется успешно, если изучение теоретического материала проходит в процессе решения задач. Этим достигается осмысленность и прочность знаний учащихся. Большое количество разнообразных задач на применение алгебры в геометрии, физике, технике и т.д. помогает учащимся понять практическую необходимость изучения алгебры. ЦЕЛИ И ЗАДАЧИ ПРОГРАММЫ Изучение математики на ступени основного общего образования направлено на достижение следующих целей: овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования; интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе; ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей; формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов; воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса. Место предмета На изучение предмета в учебном плане школы отводится 3 часа в неделю, итого 102 часа за учебный год. Количество контрольных работ - 6 РЕЗУЛЬТАТЫ ОБУЧЕНИЯ Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достичь все учащиеся, оканчивающие 9 класс, и достижение которых является обязательным условием положительной аттестации ученика за курс 9 класса. Организация образовательного процесса Основная форма организации образовательного процесса – классно-урочная система. Предусматривается применение следующих технологий обучения: традиционная классно-урочная игровые технологии элементы проблемного обучения технологии уровневой дифференциации здоровье сберегающие технологии ИКТ Преобладающие формы организации учебной работы учащихся: фронтальная, индивидуальная, реже групповая. Текущий контроль осуществляется с помощью опросов, компьютерных тестов, самостоятельных и контрольных работ. ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ ОСНОВНОЙ ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ Алгебра Алгебраические выражения, Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных, входящих в алгебраические выражения. Подстановка выражений вместо переменных, Равенство буквенных выражений. Тождество, доказательство тождеств. Преобразования выражений. Свойства степеней с целым показателем. Многочлены. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формую суммы кубов и разности. Разложение многочлена на множители. Квадратный трехчлен. Выделение полного квадрата в квадратном трехчлене. Теорема Виста. Разложение квадратного трехчлена на линейные множители. Многочлены с одной переменной. Степень многочлена. Корень многочлена. Алгебраическая дробь Сокращение дробей. Действия с алгебраическими дробями. Рациональные выражения и их преобразования, Свойства квадратных корней и их применение в вычислениях. Уравнения и неравенства. Уравнение с одной переменной. Корень уравнения. Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения. Решение рациональных уравнений. Примеры решения уравнений высших степеней; методы замены переменной, разложения на множители. Уравнение с двумя переменными; решение уравнения с двумя переменными. Система уравнений; решение системы. Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением. Уравнение с несколькими переменными. Примеры решения нелинейных систем. Примеры решения уравнений в целых числах. Неравенство с одной переменной. Решение неравенства. Линейные неравенства с одной переменной и их системы. Квадратные неравенства. Примеры решения дробно-линейных неравенств. Числовые неравенства и их свойства. Доказательство числовых и алгебраических неравенств. Переход от словесной формулировки соотношений между величинами к алгебраической. Решение текстовых задач алгебраическим способом. Числовые последовательности. Понятие последовательности. Арифметическая и геометрическая прогрессии. Формулы общего члена арифметической и геометрической прогрессий, суммы первых нескольких членов арифметической и геометрической прогрессий. Сложные проценты. Числовые функции. Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства. Чтение графиков функций. Функции, описывающие прямую и обратную пропорциональную зависимости, их графики. Линейная функция, ее график, геометрически!! смысл коэффициентов. Гипербола. Квадратичная функция, се график, парабола. Координаты вершины параболы, ось симметрии. Степенные функции с натуральным показателем, их графики. Графики функций; корень квадратный, корень кубический, модуль. Использование графиков функций для решения уравнений и систем. Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы. Параллельный перенос графиков вдоль осей координат и симметрии относительно осей. Координаты. Изображение чисел точками координатной прямой. Геометрический смысл модуля числа. Числовые промежутки: интервал, отрезок, луч. Формула расстояния между точками координатной прямой. Декартовы координаты на плоскости; координаты точки. Координаты середины отрезка, Формула расстояния между двумя точками плоскости. Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых. Уравнение окружности с центром в начале координат и в любой заданной точке. Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с двумя переменными их систем. Элементы комбинаторики, статистики и теории вероятностей Доказательство. Определения, доказательства, аксиомы и теоремы; следствия. Необходимые и достаточные условия. Контрпример. Доказательство от противного. Прямая и обратная теоремы. Понятие об аксиоматике и аксиоматическом построении геометрии. Пятый постулат Евклида и его история. Множества и комбинаторика. Множество. Элемент множества, подмножество. Объединение и пересечение множеств. Диаграммы Эйлера. Примеры решения комбинаторных задач: перебор вариантов, правило умножения. Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результатов измерений. Понятие о статистическом выводе на основе выборки. Понятие и примеры случайных событий, Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности. ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ В результате изучения математики ученик должен Знать - понимать: существо понятия математического доказательства: пример доказательств; существо понятия алгоритма; примеры алгоритмов: как используются математические формулы, уравнения и неравенства: примеры их применения для .решения математических и практических задач: как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания; как потребности практики привели математическую науку к необходимости расширения понятия числа; вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов; каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждении о них, важных для практики; смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации. Алгебра уметь составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные; выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений; применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни; решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы; решать линейные и квадратные неравенства с одной переменной и их системы; решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи, изображать числа точками на координатной прямой; определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейной неравенства; распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы не скольких первых членов; Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей; определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств; описывать свойства изученных функций, строить их графики; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах; моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры; Описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций; интерпретации графиков реальных зависимостей между величина ми. Элементы комбинаторики, статистики и теории вероятностей. уметь извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики; решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения; вычислять средние значения результатов измерений; находить частоту события, используя собственные наблюдения и готовые статистические данные; находить вероятности случайных событии в простейших случаях; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: анализа реальных числовых данных, представленных в виде диаграмм, трафиков, таблиц; решения практических задач в повседневной и профессиональной деятельности с использованием действии с числами, процентов, длин, площадей, объемов, времени, скорости; решения учебных и практических задач, требующих систематического перебора вариантов; сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией; понимания статистических утверждений. Учебно-тематический план (3 часа в неделю, всего 102 часа) № п/п Раздел, название урока в поурочном планировании Планируемый результат Контроль знаний учащихся Коли- чество часов Дата Корректи- ровка По плану фактическая 1 2 3 Повторение 7-8 класс В результате повторения учащиеся научатся применять свойства квадратных корней для упрощения выражений и вычисления корней; формировать вопросы, задачи, создавать проблемную ситуацию Уметь: использовать формулы корней квадратного уравнения; проводить замену переменной; решать квадратные уравнения и уравнения, получившиеся из замены; решать биквадратные уравнения Проблемные задания, фронтальный опрос Урок обобщения и систематизации знаний 3 2.09 4.09 6.09 Неравенства и систем неравенств 16 4 5 6 §1 Линейные и квадратные неравенства. В результате повторения учащиеся должны Уметь: - решать простейшие линейные неравенства; - отмечать на числовой оси решение неравенства - правильно найти ответ в виде числового промежутка; решать неравенства, используя метод интервалов Знать алгоритм решения неравенств. Обучающий урок. СР обучающего характера. Урок практикум. СР Фронтальный опрос Уроки обобщения и систематизации знаний Индивидуальные задания 3 9.09 11.09 13.09 7 Контрольная работа (№8 за курс 8 класса) Уметь применять изученный теоретический материал при выполнении письменной работы. Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 16.09 № п/п Раздел, название урока в поурочном планировании Планируемый результат Контроль знаний учащихся Коли- чество часов Дата Корректи- ровка По плану фактическая 8 9 10 11 12 § 2 Рациональные неравенства. Уметь: Решать рациональные неравенства методом интервалов, решать системы рациональных неравенств. Знать: Способы решения линейных, квадратных, рациональных и систем рациональных неравенств. Изучение и первичное закрепление новых знаний (беседа); практическая работа ; МД. Взаимный и индивидуальный контроль. 5 18.09 20.09 23.09 25.0927.09 13 14 § 3 Множества и операции над ними. Уметь находить на числовом множестве разность множеств, дополнение до множества, пересечение и объединение множеств. Знать Подмножество, множество, элементы множества, круги Эйлера, разность множеств, дополнение до множества, числовые множества, пересечение и объединение множеств, совокупность Комбинированный Фронтальный опрос Взаимопроверка в парах Урок обобщения и систематизации знаний 2 30.09 2.10 15 16 17 18 § 4 Системы рациональных неравенств. Уметь: Решать простейшие линейные и квадратные неравенства , решать неравенства ,используя графики, решать рациональные неравенства методом интервалов, решать системы рациональных неравенств Знать: Правила равносильного преобразования неравенств. Способы решения линейных, квадратных, рациональных и систем рациональных неравенств. Обучающий урок. Урок практикум. Самостоятельная работа обучающая. Групповой контроль, самоконтроль 4 4.10 7.10 9.10 11.10 19 Контрольная работа № 1. Уметь применять изученный теоретический материал при выполнении письменной работы. Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 14.10 № п/п Раздел, название урока в поурочном планировании Планируемый результат Контроль знаний учащихся Коли- чество часов Дата Корректи- ровка По плану фактическая Глава 2. Системы уравнений. 15 20 21 22 23 §5 Основные понятия. Уметь: решать линейные, квадратные, рациональные уравнения и их системы; составлять уравнения по условию задачи; использовать для приближённого решения уравнений графический метод; изображать на координатной плоскости множества решений простейших уравнений и их систем. Знать: Равносильные Преобразование уравнении и неравенств с двумя переменными. Алгоритм метода подстановки. Обучающий урок. Урок практикум. Самостоятельная работа обучающая. Групповой контроль, самоконтроль. 4 16.10 18.10 21.10 23.10 24 25 26 27 28 § 6 Методы решения систем уравнении Усвоение нового материала в процессе решения задач. С/Р обучающего характера с проверкой на уроке. Самоконтроль. 5 25.10 28.10 30.10 1.11 4.11 29 30 31 32 33 § 7 Системы уравнении как математическая модель реальных ситуации. Уроки – практикумы. Самостоятельная работа. Индивидуальный контроль.. 5 6.11 8.11 11.11 12.11 15.11 34 Контрольная работа № 2. Уметь применять изученный теоретический материал при выполнении письменной работы. Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 18.11 Глава 3. Числовые функции 25 35 36 37 38 §8 Определение числовой функции. Область определения, область значений функции. Знать определение функции, области определения и области значения функции. Уметь находить область определения и область значения функции Урок ознакомления с новым материалом Урок закрепления изученного Урок применения знаний и умений Урок обобщения и систематизации знаний 4 20.11 22.11 25.11 27.11 39 40 §9 Способы задания функций. Знать определение функции, области определения и области значения функции. Уметь: при задании функции применять различные способы: аналитический, графический, табличный, словесный. Уроки – практикумы. Самостоятельная работа. 2 29.11 2.12 41 42 43 44 §10 Свойства функций. Знать определение возрастающей и убывающей функции на промежутке; условия возрастания и убывания функции. Уметь строить графики степенной функции при различных значениях показателя; описывать Усвоение нового материала в процессе решения задач. С/Р обучающего характера с проверкой на уроке. Самоконтроль. 4 4.12 6.12 9.12 11.12 45 46 47 §11 Четные и нечетные функции. Знать определение чётной и нечётной функции; как расположен график четной и нечетной функции. Уметь по формуле определять четность и нечетность функции; приводить примеры этих функций; строить график функции , описывать по графику свойства функции Фронтальный опрос работа по готовым графикам Урок ознакомления с новым материалом Урок закрепления изученного Урок применения знаний и умений Поисковый 3 13.12 16.12 18.12 48 Контрольная работа №3 Уметь применять изученный теоретический материал при выполнении письменной работы. Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 20.12 49 50 51 52 §12 Функции у=хп ( п Є N).Их свойства и графики. Знать :Определение числовой функции, области определения и области значения функции. О понятии степенной функции с натуральным показателем, о свойствах и графике функции. О понятии степенной функции с отрицательным целым показателем, о свойствах и графи функции. Уметь: Определять графики функции с чётным и нечётным показателем и с отрицательным показателем. Строить графики Степенных функции с любым показателем степени, читать свойства по графику функции. Строить график корня третьей степени, по графику описать свойства функции корня третьей степени. Практический урок + объяснение. Урок усвоения новых знаний 4 23.12 25.12 27.12 30.12 53 54 55 §13 Функции у= х-п ( п Є N) и их свойства и графики. Усвоение нового материала в процессе решения задач. С/Р обучающего характера с проверкой на уроке. 3 13.01 15.01 17.01 56 57 58 §14 Функция у=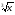 её свойства и график. Урок – исследование. Урок контроля, оценки и коррекции знаний учащихся. Тематический контроль. 3 20.01 22.01 24.01 59 Контрольная работа №4. Уметь применять изученный теоретический материал при выполнении письменной работы. Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 27.01 Глава 4 Прогрессии 16 60 61 62 63 § 15 Числовые последовательности Знать определение числовой последовательности. Иметь представление о способах задания числовой последовательности. Уметь приводить примеры последовательностей; определять член последовательности по формуле Урок ознакомления с новым материалом Урок закрепления изученного Дифференцированные карточки по теме Проверочная работа 4 29.01 31.01 3.02 5.02 64 65 66 67 68 §16 Арифметическая кая прогрессия. Знать определение и формулу n – го члена арифметической прогрессии, характеристическое свойство арифметической прогрессии. Уметь применять при решении задач указанные формулы. Урок ознакомления с новым материалом Урок закрепления изученного Урок применения знаний и умений Урок ознакомления с новым материалом Урок закрепления изученного Индивидуальный опрос Математический диктант 5 7.02 10.02 12.02 14.02 17.02 69 70 71 72 73 74 §17 Геометрическая прогрессия Знать определение Геометрическая прогрессия, знаменатель геометрической прогрессии, формула n-го члена геометрической прогрессии, характеристическое свойство геометрической прогрессии Уметь применять при решении задач указанные формулы Урок ознакомления с новым материалом Урок закрепления изученного Урок ознакомления с новым материалом Урок закрепления изученного Индивидуальный опрос Математический диктант 6 19.02 21.02 24.02 26.02 28.02 3.03 75 Контрольная работа№5 Уметь применять изученный теоретический материал при выполнении письменной работы. Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 5.03 Глава 5. Элементы комбинаторики, статистики и теории вероятностей 12 76 77 78 § 18 Комбинаторные задачи. Уметь: Решать задачи по комбинаторике и вероятностные задачи жизненного содержания, применять формулы теории вероятности и статистики при решении задач Знать: как построить дерево возможных вариантов для небольшого количества вариантов. На конкретных Примерах рассмотреть основные методы решения Простейших комбинаторныхзадач. О связи между статистикой и теорией вероятностей. Основные формулы теории вероятности и статистики Урок ознакомления с новым материалом Урок закрепления изученного Исследовательский 3 7.03 10.03 12.03 79 80 81 § 19 Статистика- Дизайн информации. Урок ознакомления с новым материалом Проблемный Комбинированный 3 14.03 17.03 19.03 82 83 84 § 20 Простейшие вероятностные задачи. Уроки обобщение и систематизации знаний, уроки – практикумы, комбинированные уроки 3 21.03 24.03 26.03 85 86 § 21 Экспериментальные данные и вероятности событий. Усвоение изученного материала в процессе решения задач. Обучающий, тест. 2 28.03 31.03 87 Контрольная работа №6. Уметь применять изученный теоретический материал при выполнении письменной работы. Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 2.04 Итоговое повторение 17 88 Выражения и их преобразования Уметь: выполнять арифметические действия, сочетая устные и письменные приемы, находить значения корня натуральной степени, степени с рациональным показателем; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования. Урок обобщения и систематизации знаний 1 4.04 89 90 Выражения и их преобразования Урок применения знаний и умений 2 7.04 9.04 91 Уравнения и системы уравнений Уметь: решать линейные, квадратные, рациональные уравнения и неравенства, их системы; составлять уравнения и неравенства по условию задачи; использовать для приближённого решения уравнений и неравенств графический метод; изображать на координатной плоскости множества решений простейших уравнений, неравенств и их систем. Урок обобщения и систематизации знаний 1 11.04 92 93 Уравнения и системы уравнений Урок применения знаний и умений 2 14.04 16.04 94 Неравенства и системы неравенств Урок обобщения и систематизации знаний 1 18.04 95 97 Неравенства и системы неравенств Урок применения знаний и умений 2 21.04 23.04 98 99 Текстовые задачи Уметь: составлять уравнения и неравенства по условию задачи Урок обобщения и систематизации знаний 2 25.04 28.04 100 Функции и графики Уметь: определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков. Урок обобщения и систематизации знаний 1 2.04 101 Функции и графики Урок применения знаний и умений 1 9.05 102 Арифметическая и геометрическая прогрессии Уметь: применять при решении задач определение и формулу n – го члена арифметической прогрессии, характеристическое свойство арифметической прогрессии, формулы суммы n первых членов арифметической прогрессии; определение и формулу n – го члена прогрессии, характеристическое свойство геометрической прогрессии, формулу суммы n первых членов геометрической прогрессии. 1 16.05 Итоговая контрольная работа в форме ГИА Закрепление знаний, умений и навыков, полученных на уроках по данным темам Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. 1 23.05 Тематика контрольных работ Линейные и квадратные неравенства – 1 час Неравенства и системы неравенств -1 час. Системы уравнений -1 час. Числовые функции - 2часа. Прогрессии -1 час События. Вероятности. Статистическая обработка данных -1час Контрольные работы находятся в методическом пособии «АЛГЕБРА 9» (контрольные работы) автора - составителя Ю.П.Дудницьша под редакцией А.Г.Мордковича - Москва, Мнемозима, 2010 г., а так же контрольные работы будут составляться индивидуально. Для составления контрольных работ будут использоваться материалы для подготовки к итоговой государственной аттестации. Литература. Алгебра - 9, Учебник А.Г.Мордковича - М.: Мнемозима, 2010. «АЛГЕБРА -9» Задачник А.Г.МордковичаДЕ Тульчинской, Т.Н.Мишустиной- М.,Мнемозима, 2010 3.Алгебра 9,методтическое пособие для учителя. А.Г.Мордкович, Семенов П.В. -М.,Мнемозима,2010г. 4.Математика: сборник материалов по реализации федерального компонента государственного стандарта общего образования в общеобразовательных учреждениях/ авт- сост. Е.И. Колусева, З.С. Гребнева, - Волгоград: Учитель, 2006. 5.Оценка качества знании выпускников основной школы по математике/ Г.В. Дорофеев, Л.В. Кузнецова, Г. В. Кузнецова и др. - М.: Дрофа, 2000. 6.Сборник нормативных документов. Математика/ Сост. Э.Д. Днепров, А.Г. Аркадьев. -М.: Дрофа, 2004. 7. События. Вероятности. Статистическая обработка данных: Доп. параграфы к курсу алгебры 7 - 9 кл. общеобразовательных учреждений/ А.Г Мордкович, П.В. Семенов. -5-е изд.- М.: Мнемозина, 2008. 8. Алгебра 9 Блицопрос: Е.Е.Тульчинская. – М.: Мнемозина, 2010. – 91 с. 9. Ященко И.В., Семенов А.В., Захаров П.И. подготовка к экзамену по математике ГАИ 9 в 2011 году. Методические рекомендации. – М.: МЦНМО, 2011. – 208 с. Математика 9 класс. ГИА. Тематические тренировочные задания. Базовый уровень. Под редакцией Семенко Е. А. М.: «Экзамен». 2011. Математика 9 класс. ГИА. Тематические тренировочные задания. Повышенный уровень. Под редакцией Семенко Е. А. М.: «Экзамен». 2011. Контрольно – измерительные материалы. Алгебра: 9 класс/ Сост. Мартышова Л. И. – М.: ВАКО, 2010.