«Развитие логического мышления у учащихся 6 класса через решение комбинаторных задач на уроках математики»
 Скачать 221.92 Kb. Скачать 221.92 Kb.
|
      МКОУ Уляхинская основная общеобразовательная школа МКОУ Уляхинская основная общеобразовательная школаГусь-Хрустального района Владимирской области Обобщение опыта Тема: «Развитие логического мышления у учащихся 6 класса через решение комбинаторных задач на уроках математики» Учитель: Карева Алла Николаевна Д.Уляхино,2012 год Обобщение опыта учителя математики Каревой Аллы Николаевны Стаж работы: 15 лет Преподаваемый предмет: математика и информатика Стаж по данному предмету: 4 года Специальность по диплому: учитель математики и физики Общий педагогический стаж: 15 лет Образовательное учреждение: МКОУ Уляхинская основная общеобразовательная школа Район: Гусь-Хрустальный, Владимирской области. Имею вторую квалификационную категорию. Тема: Развитие логического мышления у учащихся 6 класса через решение комбинаторных задач на уроках математики. Условия возникновения и становления опыта. Современный мир переживает радикальные изменения: на смену техногенного типа общества идет посттехногенное общество. Главное отличие последнего состоит в изменении отношения к человеку. Посттехногенному типу общества, где человек есть субъект и главная цель, необходима принципиально новая система образования – так называемое «личностно-ориентированное образование». В связи с этим изменяются цели и задачи современной школы. В «Концепции модернизации Российского образования » преобразование общеобразовательной школы предполагает ориентацию образования не только на усвоение обучающимися определенной суммы знаний, но и на развитие их личности, их познавательных и созидательных способностей. Естественно на первый план выдвигается проблема обеспечения новых подходов к организации педагогической деятельности, акценты в которой должны быть сделаны на воспитание саморазвивающейся личности. Важнейшей предпосылкой возникновения данного опыта является неумение детей ясно и четко выражать свои мысли, неумение слушать и отвечать на поставленные вопросы, низкая мотивация и заинтересованность в обучении. Это создает большие трудности в изучении математики, делает ее недоступной и неинтересной. Очевидно, что сложившееся положение заставляет искать пути решения данной проблемы. Актуальность и перспективность опыта. На современном этапе развития общества, когда в нашу жизнь стремительно вошли референдумы и социологические опросы, кредиты и страховые полисы становится актуальность включения в школьный курс математики материала вероятностно- статистического характера. Данная тема исследования актуальна для наших детей в связи с тем, что современные школьники стали более развиты и им требуются не просто задачи на вычисление, а задачи, требующие в своём решении участия логического мышления. Такими задачами и являются задачи на комбинаторику и вероятность. Данное исследование определяет уровень логического мышления учащихся 6 класса. А выявление методов обучения решению таких задач даёт возможность выбора наиболее оптимального метода для преподавания. Также актуальность этой проблемы вытекает из противоречий, сложившихся в настоящее время в современном образовании: - противоречие между традиционным обучением и ориентацией современного образования на развитие личности; - между программными требованиями и реальным уровнем обучения; - между коллективным обучением и индивидуальным развитием личности школьника; - между снижением интереса учащихся к изучению математики и формированием качеств мышления, характерных для математической деятельности; Теоретическая база опыта. Мышление – активный процесс отражения объективного мира в понятиях, суждениях, научных теорий, гипотезах и т.д. Одним из важных компонентов мышления является логика, логическое мышление. Логика – наука о законах и операциях правильного мышления зародилась в Древней Греции. Основоположником логики по праву считают великого ученого Аристотеля. Логика лежит в основе различных наук (естественных, общественных и технических), а также в основе любого учебного предмета, изучаемого в начальной и средней школе. Эти же логические знания (формы абстрактного мышления: понятия, суждения, умозаключения) лежат в основе всякого учебного предмета, изучаемого в любом вузе, колледже, лицее, гимназии – во всех учебных заведениях, как современных, так и функционировавших в прошлые века. Логику должен знать каждый человек, чтобы мыслить правильно, т.е. определенно, непротиворечиво, доказательно, четко, и уметь излагать свои мысли понятным языком. В своём опыте я опираюсь на работы психологов Ж.Пиаже и Е.Фишбейна.В работах «Речь и мышление ребёнка» и «Психология интеллекта» они показывают, что человек изначально плохо приспособлен к вероятностной оценке, к осознанию и верной интерпретации вероятностно-статистической информации. Их исследования показывают, что наиболее благоприятен для формирования вероятностных представлений и развития логического мышления возраст 11-12 лет. Это 5-6 классы. Ведущая педагогическая идея. В среднем звене школы заметно падение интереса к процессу обучения в целом и в частности к математике. На уроках математики проводимых по привычной схеме и на традиционном материале у ученика создаётся ощущение непроницаемой стены между изучаемым объектом и окружающим миром. Именно вероятностно-статистическая линия , изучение которой невозможно без опоры на процессы, наблюдаемые в окружающем мире, на реальный жизненный опыт, способна содействовать как к возвращению интереса к предмету «математика», так и к развитию личности самого ребёнка, его логического мышления. Новизна опыта. По современным стандартам и программам математического образования вероятностно-статистическая линия по учебникам Н.Я.Виленкина изучается интегрировано. Новизна данного опыта в том, что данный материал изучается блоком. На данную тему отводится 4 часа в конце года, за счёт резервного времени. Адресность опыта. Данный опыт приемлем для всех категорий педагогов: от педагогов с высоким уровнем мастерства до начинающих педагогов. Область применения: 6 классы всех образовательных учреждений. Технология опыта. Цель педагогической деятельности: Развитие логического мышления учащихся 6 класса через решение комбинаторных задач на уроках математики. Исходя из этого , ставлю следующие задачи: 1.Разработать уроки на решение комбинаторных задач в 6 классе. 2.Провести уроки на решение комбинаторных задач в 6 классе одним блоком. 3.Продиагностировать уровень развития логического мышления у учащихся 6 класса. Этапы педагогической деятельности: 1.Констатирующий этап. На данном этапе были проведены и обработаны тесты на оценку логического мышления у учащихся 6 класса. А также были даны задания на выборочное решение задач.(обычные, комбинаторные) А)Тест на изучение логического мышления. Учащимся зачитывается ряд слов, которые они должны запомнить, причём эти слова составляют часть предложений. Вторые части зачитываются чуть позже. Учитель читает слова первого ряда с 5-секудным интервалом. После 20 секундного перерыва зачитываются слова второго ряда. Учащиеся должны записать предложения, составленные из слов первого и второго рядов. Первый ряд Второй ряд Барабан пожар Села на цветок столица родины Трусость железо и золото Произошёл на фабрике висел на стене Москва пчела Металлы мальчик Принёс книгу плохое качество Оценивание: 0-2-низкий уровень 3-5-средний уровень 6-7-высокий уровень Результаты: Количество человек в классе-4 Количество учащихся, выполнявших тест-4 Низкий уровень-1 человек Средний уровень-2 человека Высокий уровень-1 человек Б)Решение задач на выбор. Учащимся предлагается две задачи и решить их. Задача 1.В одном пакете ¾ кг конфет, а в другом-на 1/5 меньше, чем в первом. Сколько конфет в обоих пакетах? Ответ: 26/20 кг Задача 2. В кафе предлагают два первых блюда: борщ, рассольник- и четыре вторых: гуляш, котлеты, сосиски, пельмени. Укажите все разнообразные обеды из двух блюд. Ответ:8 вариантов. Оценивание: 0задач-низкий уровень 1 задача-средний уровень 2 задачи-высокий уровень Результаты: Количество человек в классе-4 Количество решавших задачи-4 Низкий уровень-0 Средний уровень-3 Высокий уровень-1 2.Формирующий этап. На данном этапе проводятся уроки в 6 классе на решение комбинаторных задач. Повышение уровня логического мышления, уровня знаний и интереса к математике достигается следующим образом:. 1.При актуализации знаний на первом уроке перед учащимися ставится проблема: В старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. Ребята, с какой проблемой сталкивается добрый молодец на перепутье? Ответ учащихся: с проблемой выбора дальнейшего пути движения. -Верно! А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Это сделать очень трудно не потому, что его нет или оно одно и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был оптимальный. Оказывается существует целый раздел математики, именуемый комбинаторикой, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. 2.Новый материал-«Способы решения комбинаторных задач(таблица вариантов, дерево вариантов, правило умножения)» излагается учителем на первом уроке. Параллельно решается задача на составление флагов из цветов флага РФ. На следующих уроках идёт закрепление этих правил , с помощью решения разнообразных задач, содержащих жизненные ситуации. 3.Используются различные формы обратной связи.Это: -устный опрос -самостоятельная работа в группах -индивидуальная самостоятельная работа. 4.Разнообразие домашнего задания .Это: -решение задач, предложенных учителем -составление синквейна -составление комбинаторных задач самими учащимися Учащиеся охотно составляют задачи. Например: А).Имеется чёрный хлеб, белый хлеб, сыр, варенье. Сколько разнообразных бутербродов можно приготовить? Составить дерево вариантов. Б).Составить все возможные варианты двухзначных чисел, используя цифры 1, 6, 8 не более одного раза. Использовать таблицу вариантов. 5.Также для повышения уровня логического мышления использую на уроках исторический материал (история возникновения комбинаторики как науки). 6.Использую на уроках мультимедийные технологии, наглядные пособия, что повышает интерес учащихся к задачам 7.Одним из средств активации мыслительной деятельности, внимания, умственного развития является игра. Игра помогает школьникам раскрепостить воображение, развивает наблюдательность, смекалку, интеллект, логическое мышление. На последнем уроке проводится игра-соревнование «Своя игра» между двумя командами. Разработки уроков прилагаются Презентации размещены на мини-сайте ns- портал https://nsportal.ru/shkola/algebra/library/prezentaciya-k-uroku-v-6-klasse-reshenie-kombinatornyh-zadach. 3.Контролирующий этап. Повторное проведение и обработка теста на развитие логического мышления. Повторное задание на решение задач. Результаты: А)Психодиагностический тест Низкий уровень-0 Средний уровень-1 Высокий уровень-3 Б)Решение задач. Низкий уровень-0 Средний уровень-1 Высокий уровень-3 Результативность Сравнение результатов констатирующего этапа с результатами контролирующего этапа представлено в диаграмме. А)Психодиагностический тест Б)Решение задач По результатам исследования можно сказать следующее: если применять данную методику решения комбинаторных задач в 6 классе, то повышается уровень логического мышления учащихся, формируется творческая личность учащегося повышается интерес к предмету. Приложение 1 Урок 1 Тема: Решение комбинаторных задач Цель: начать формировать умения решать простейшие комбинаторные задачи. Задачи:
ХОД УРОКА I Актуализация опорных знаний. Слово учителя: в старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. Ребята, с какой проблемой сталкивается добрый молодец на перепутье? Ответ учащихся: с проблемой выбора дальнейшего пути движения. Слово учителя: Верно! А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Это сделать очень трудно не потому, что его нет или оно одно и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был оптимальный.  Оказывается существует целый раздел математики, именуемый комбинаторикой, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. II. Изучение нового материала. Слово учителя: задачи, которые мы сегодня будем решать помогут вам творить, думать необычно, оригинально, смело, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности и идти через невозможное вперед.Комбинаторная задача – задача, в которой идет речь о тех или иных комбинациях объектов. Учащимся раздаются цветные полоски (белый, синий, красный) и предлагается из них составить флаг РФ. Затем задаются вопросы исторического характера.  Что означает каждый цвет? Значение цветов флага России: белый цвет означает мир, чистоту, непорочность, совершенство; синий – цвет веры и верности, постоянства; красный цвет символизирует энергию, силу, кровь, пролитую за Отечество. Оказывается, есть государства, где флаги имеют такие же цвета.  Видим, что от перестановок цветных полосок, можно получить другой флаг. Как подсчитать, сколько таких флагов мы можем составить из трех цветных полосок? Решение этой задачи можно записать тремя способами:
 3.Правило умножения 1 полоса 3 способа 2 полоса 2 способа 3 полоса 1 способ 3 ∙ 2 ∙ 1 = 6 Ответ: 6 способов III Выполнение упражнений.
IV Итог урока. Домашнее задание. Сколько трехзначных чисел можно составить из цифр 1, 3 и 5? Решите задачу различными способами Урок 2. Тема: Решение комбинаторных задач. Цель: продолжить формирование умений решать простейшие комбинаторные задачи практического содержания. Задачи:
Из урока в урок я не перестаю повторять, а вы убеждаетесь в том, что наш мир полон математики. И сегодня мы продолжим исследовать на предмет выявления (если можно так выразиться) математики вокруг нас. 1) Устный опрос.
В это время два ученика оформляют на доске решение домашних задач. 2) Работа в группах. Класс разбит на 2 группы. Каждая группа получает задания, на решение которых отводится 10 мин. После выполнения заданий каждая группа представляет свое решение. 1 группа. 1 задание В субботу в 5 «А» классе 5 уроков: физкультура, русский язык, литература, ИЗО, математика. Сколько можно составить вариантов расписания на день? Сколько можно составить вариантов расписания на день, зная, что математика – последний урок? 2 задание Путешественник хочет выехать на своей машине из города А, посетить города В, С и D, после чего вернуться в город А. Какими путями можно это сделать? На рисунке схема путей, связывающих города. Какой из вариантов самый оптимальный? 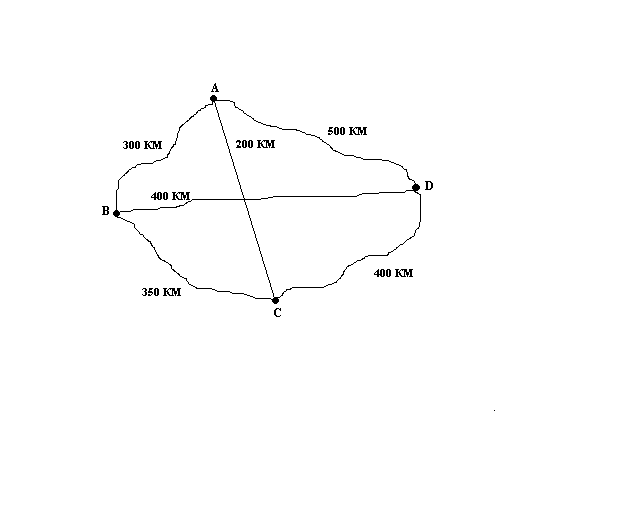 2 группа. 1 задание Участники лыжных соревнований стартуют с интервалом в 30 секунд. Чтобы определить порядок старта, спортсмены тянут жребий, определяющий номер старта. Сколько существует различных последовательностей выхода лыжников на старт, если в соревнованиях принимает участие 6 лыжников. Через какой промежуток времени все спортсмены будут на лыжне? 2 задание Хоккейная комбинация. На поле 5 игроков. Начал комбинацию игрок № 1, продолжили игроки с другими номерами, а забил гол игрок № 5. Каждый хоккеист ударил по шайбе только один раз. На рисунке с помощью стрелок изображен один из возможных вариантов передачи шайбы между игроками в данной комбинации. Изобразите в тетради все другие возможные варианты передачи шайбы. 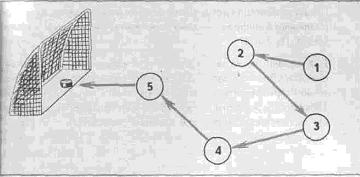 3) Представление решений. 4) Итоги 5) Домашнее задание. а) Решить любые три задачи. 1. Сколько трёхзначных чисел можно составить, используя цифры 3 и 5? 2. Андрей зашел в магазин, чтобы купить майки. В магазине оказались майки четырех цветов: белые, голубые, красные, черные. а) Сколько вариантов покупки есть у Андрея, если он хочет купить две майки? Подсказка: обозначьте цвета маек буквами Б, Г, К, Ч. Составьте дерево возможных вариантов б) Сколько вариантов покупки есть у Андрея, если он хочет купить две майки разного цвета? 3. В классе три человека хорошо поют, двое других играют на гитаре, а еще один умеет показывать фокусы. Сколькими способами можно составить концертную бригаду из певца, гитариста и фокусника? 4. Наташа сшила кукле десять разных платьев, а Даша сшила своему мишке трое штанишек и четыре футболки. Как вы думаете, у кого больше разных нарядов – у куклы или у мишки? 5. Для начинки пирогов у Наташи есть капуста, яйца, зелень лук и клубничное варенье. Сколько различных начинок можно приготовить из этих продуктов? При этом не надо забывать, что пироги должны быть вкусными. Вряд ли кто из вас захочет съесть пирог с начинкой из капусты с клубничным вареньем. 6. Служитель зоопарка должен дать зайцу два различных овоща. Сколькими различными способами он может это сделать, если у него есть морковь, свекла и капуста? 7. В алфавите племени УАУА имеются всего две буквы – «а» и «у». Сколько различных слов по три буквы в каждом можно составить, используя алфавит этого племени? 8. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Сколько различных вариантов завтрака может выбрать Вова? б) Составить синквейн к слову «комбинаторика» ПРАВИЛА НАПИСАНИЯ СИНКВЕЙНА 1 строчка – одно слово – название стихотворения, тема, обычно существительное. 2 строчка – два слова (прилагательные или причастия). Описание темы, слова можно соединять союзами и предлогами. 3 строчка – три слова (глаголы). Действия, относящиеся к теме. 4 строчка – четыре слова – предложение. Фраза, которая показывает отношение автора к теме в 1-ой строчке. 5 строчка – одно слово – ассоциация, синоним, который повторяет суть темы в 1-ой строчке, обычно существительное. Примерный ответ. Комбинаторика Интересная, непознанная. Изучать, понимать, перебирать. Присутствует во всех областях. Урок 3. Тема: Решение комбинаторных задач. Цель: продолжить формирование умений решать простейшие комбинаторные задачи практического содержания. Задачи: обобщить и систематизировать знания и умения учащихся по теме развивать логическое мышление учащихся формировать познавательный интерес к предмету Ход урока: 1) Из истории науки «Комбинаторика» (сообщение ученика) Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов, - возникла в XII веке. Еще в доисторическую эпоху люди сталкивались с комбинаторными задачами. Выбирать и расположить предметы в определенном порядке, отыскивать среди разных рассположений наилучшее – вот задачи, решаемые в быту, на охоте или в сражениях. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют "сочетания". В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. По мере усложнения производственных и общественных отношений задачи усложнялись. Комбинаторные задачи встречались, как игры в досуге. Наряду с состязаниями в беге, метании диска, кулачными боями появлялись игры, требовавшие умение мыслить, рассчитывать, составлять планы, опровергать планы противника. Со временем игры усложнились: появились нарды, карты, шашки и шахматы. В таких играх приходилось рассчитывать различные ситуации, комбинации сочетания фигур. При тайных переписках дипломаты стали применять шифры, которые были основаны на различных перестановках букв, чисел, заменах букв с использованием ключевых слов и т. д. Комбинаторика как наука стала развиваться в XIII в. параллельно с возникновением теории вероятностей. Первые научные исследования по этой теме принадлежат итальянским ученым Дж. Кардано, Н. Чарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б.Пискамо (1623-1662) и П. Ферма. Комбинаторику, как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика». Значительный вклад в развитие комбинаторики внес Л. Эйлер. Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX в. За последние годы комбинаторика переживает период бурного развития, связанного с общим повышением интереса к проблемам дискретной математики. Комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний; для составления планов производства и реализации продукции. Установлены связи между комбинаторикой и задачами линейного программирования, статистики и т. д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории информации. Значительную роль комбинаторные методы играют и в чисто математических вопросах — теории групп и их представлений, изучении оснований геометрии, неассоциативных алгебр и т. д. 2) Повторение Какие способы решения комбинаторных задач мы знаем? Дерево вариантов, табличный, правило умножения. Сравним эти способы.
3) Выполнение упражнений. 1. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута? 2. Человек, пришедший в гости, забыл код, открывающий дверь подъезда, но помнил, что он составлен из нулей и единиц и содержит четыре цифры. Сколько вариантов кода в худшем случае ему придется перебрать, чтобы открыть дверь? 3. Витя, Толя и Игорь купили вместе интересную книгу и решили ее читать по очереди. Выпишите все варианты такой очереди. Сколько есть вариантов, в которых Игорь на первом месте? Витя не на последнем месте? 4. Имеется ткань двух цветов: голубая и зеленая – и требуется обить диван, кресло и стул. Сколько существует различных вариантов обивки этой мебели? 3) Самостоятельная работа.
4) Итог урока. Математика повсюду – Глазом только поведешь И примеров сразу уйму Ты вокруг себя найдешь… 5) Домашнее задание Составить комбинаторные задачи практического содержания. Урок 4 Игра «Своя игра» Цель игры: Обобщить и систематизировать знания по комбинаторике Правила игры: В игре участвуют две команды. На игровом поле размещены ячейки. Поле разбито на пять секторов. В каждом секторе пять ячеек. Каждая имеет свою стоимость. Команда выбирает ячейку и отвечает на вопрос этой ячейки. Ход игры
1.Числовые ребусы 10. 20. 30. 40. 50. 95 95 * * 0 12 * ,5 * 5, * 7 ** ** * 8 4* 3, * 4 *, 0 * *5 **5 6 * 7, 3 8 6, 0 0 1 ** ** * * * * ** * *3* 0 2.Числовые ряды Определить правила и продолжить ряд: 10.- 23, 27, 31, 35…( + 4)
30.- 14, 17, 18, 21…( следующее,+3)
3.Задача-шутка. 10.Сколько концов у двух палок, у трёх палок, у пяти с половиной палок? 20.Какой математический знак нужно поставить между 5 и 6, чтобы полученное число было больше 5 но меньше 6. 30.Крышка стола имеет 4 угла. Один угол отпилили. Сколько углов осталось? 40.У меня две монеты на общую сумму 15 копеек. Одна из них не пятак. Что это за монеты? 50.Найдите два в квадрате, три в квадрате, угол в квадрате. 4.Логические задачи. 10.На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод? 20Сколько всего двухзначных чисел можно составить из цифр 7,4 и 5 при условии, что они в записи числа не повторяются? 30.У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов? 40. Учащиеся 6 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 24 человека? 50.При встрече 8 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий? 5.Ребусы в картинках 10.  Задача 20. 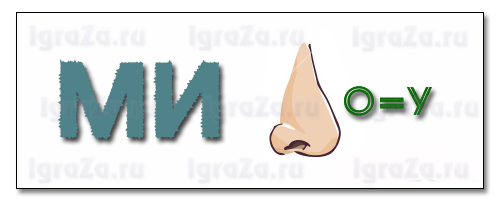 Минус. 30. 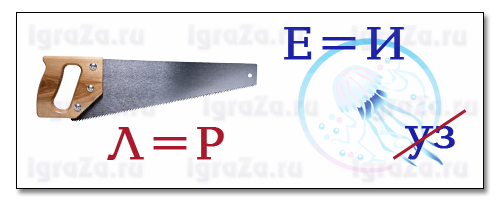 Пирамида. 40  Число 50. 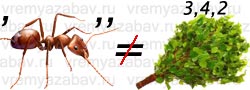 Уравнение. Литература:
М. «Владос» 2006г. Е.И.Рогов.
г. З.А.Михайлова. 7. «Математическая смекалка» М. «Наука» Б.А.Кордемский. 8. «Логические основы математики» М. « Дрофа». А.Д. Гетманова. |