Учитель
|
Кузнецова Светлана Александровна
|
Класс
|
10
|
Раздел
|
Подготовка к ЕГЭ. Решение задач с процентами
|
Результаты
обучения
по разделу
|
Личностные
|
Метапредметные
|
Предметные
|
Умение ясно, точно, грамотно излагать свои мысли.
Креативность мышления,инициатива
активность при решении математических задач
Умение контролировать процесс и результат учебной математической деятельности
|
Представление о методах математики как универсальном языке науки , о средстве моделирования явлений и процессов.
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах
Уметь применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач
Умение самостоятельно ставить цели, создавать алгоритмы решений
Умение планировать и осуществлять свою деятельность
|
Умение работать с математическим текстом.
Владение базовым понятийным аппаратом
Овладение практически-значимыми математическими умениями и навыками
Применение изученных методов при решении задач из различных разделов курса
|
Система задач
|
Олимпиадные
|
Практико-ориентированные
|
Творческие/
исследовательские
|
Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки?
|
Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг.
|
Товар m дороже товара n на 60%. На сколько процентов n дешевле m?
|
Имелось два разных сплава меди. Процент содержания меди в первом сплаве был на 40% меньше, чем во втором. Затем их сплавили вместе и получили сплав, содержащий 36% меди. Определите процентное содержание меди в первом и во втором сплавах, если известно, что меди в первом сплаве было 6 кг, а во втором – 12 кг
|
Кусок сплава меди с оловом массой 15кг содержит 20% меди. Сколько чистой меди необходимо добавить к этому сплаву, чтобы новый сплав содержал 40% олова?
|
Решить задачу в общем виде.
Увеличили число а на р %. На сколько процентов надо уменьшить полученное число, чтобы получить а
|
Вычислите вес и процентное содержание серебра в сплаве с медью, зная, что сплавив его с 3 кг чистого серебра, в результате получат сплав, содержащий 90% серебра, а сплавив его с 2 кг сплава, содержащего 90% серебра, получат сплав с 84% содержанием серебра
|
На сколько процентов уменьшится объём кругового конуса, если уменьшить его высоту на 20%?
|
Предприятие работало два года. В первый год выработка возросла на Р%, во второй на 10% больше, чем в первый. Определить на сколько процентов увеличилась выработка за второй год, если за два года она увеличилась на 48,59 %.
|
ТЕХНОЛОГИЧЕСКАЯ КАРТА РАБОТЫ НАД ЗАДАЧЕЙ
|
Формулировка задачи
|
Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг.
|
Решение задачи
|
400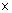 0.18 = 72 (кг) – масса воды в смеси; 0.18 = 72 (кг) – масса воды в смеси;
400 – 72 = 328 (кг) – масса сухого цемента в смеси;
18 + 2 = 20 (%) – влажность привезенной смеси;
100 – 20 = 80 (%) – сухого цемента в смеси;
328 : 0,8 = 410 (кг) – масса привезенной смеси.
Ответ: масса привезенной смеси равна 410 кг.
|
Основные этапы работы над задачей.
|
Цель этапа
|
Содержание педагогического взаимодействия
|
Деятельность
учителя
|
Деятельность учащихся
|
Познавательная
|
Коммуникативная
|
Регулятивная
|
Постановка учебной задачи
|
создание проблемы
|
текст задачи проектирует на доску
|
фиксируют проблему
|
проявляют готовность активно участвовать в учебно-познавательной деятельности
|
понимают смысл учебного задания, принимаюя его цель
|
Исследование проблемы
|
анализ условия,
поиск решения задачи
|
предлагает поработать в парах, обсудить возможные пути решения проблемы
|
Учащиеся проводят анализ условия задачи, идет поиск способа решения
|
принимают участие в работе пары,используя для этого речевые и другие коммуникативные
средства, ведут диалог, направленный на решение проблемы
|
Формулируют в паре идею решения задачи
|
Моделирование
|
составление математической модели проблемы
|
задает наводящие вопросы :
-Как вы понимаете выражение: влажность смеси составляет 18%?
-Чему равно количество воды в смеси?
Чему стала равна влажность смеси после перевозки?
Изменилась ли масса сухого цемента после перевозки?
|
делают вывод,что задачу можно решить с опорой на тему - нахождение числа по его проценту
|
отвечают на вопросы учителя
- В смеси содержится 18% воды
- 400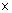 0.18(кг) 0.18(кг)
- 18%+2%
-Нет
делают вывод,что задачу можно решить с опорой на тему - нахождение числа по его проценту
|
планируют решение
|
Решение проблемы
|
оформление
решения задачи
|
предлагает изложить решение задачи на доске
|
задача свелась к нахождению числа по его проценту (ранее изучено ) в новой ситуации
|
оформляют решение задачи на доске, проговаривая этапы решения
1)400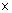 0.18 = 72 (кг) – масса воды в смеси; 0.18 = 72 (кг) – масса воды в смеси;
2)400 – 72 = 328 (кг) – масса сухого цемента в смеси;
3)18 + 2 = 20 (%) – влажность привезенной смеси;
4)100 – 20 = 80 (%) – сухого цемента в смеси;
5)328 : 0,8 = 410 (кг) – масса привезенной смеси.
Ответ: масса привезенной смеси равна 410 кг.
|
волевая саморегуляция, коррекция в записи,
самоконтроль решения
|
Поиск другого способа решения
|
поиск возможно более эффективного способа решения
|
предлагает найти иной способ решения
Приглашает ученика реализовать способ решения на доске
|
ищут и выделяют необходимую информацию, выбирают эффективный способ решения
|
ответ учащихся:
-Можно эту задачу решить с помощью пропорции
Записывает новый способ решения на доске,комментирует решение
Пусть х кг – масса привезенной смеси
1)400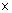 0.18 = 72 (кг) – масса воды в смеси; 0.18 = 72 (кг) – масса воды в смеси;
2)400 – 72 = 328 (кг) – масса сухого цемента в смеси;
( х – 328) кг – 20%
х кг – 100%
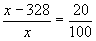 ; ; 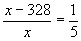 ; ; 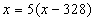 ; ; 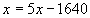 ; ; 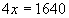 ; ; 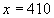 Ответ: масса привезенной смеси равна 410 кг. Ответ: масса привезенной смеси равна 410 кг.
|
волевая саморегуляция,
прогнозирование совпадения результата рещения задачи 1 и 2 способами,
коррекция в записи,
самоконтроль решения
|
Анализ
|
анализ способов решения задач
|
предлагает определить какой способ на их взгляд более рациональный
|
Учащиеся сравнивают два решения, анализируют их
|
приходят к выводу, что второе решение более громоздкое.
|
Оценивают результаты
|
Контроль усвоения
|
контроль усвоения
|
Предлагает решить по вариантам задачу самостоятельно ,найти несколько способов решения:
Проецирует текст на доску
1.Сколько литров воды надо добавить к 20 литрам пятипроцентного раствора соли, чтобы получить 4-хпроцентный раствор?
2. В 30 кг пятипроцентного раствора соли добавили воды, при этом получили 1,5-процентный раствор соли. Сколько кг воды добавили?
|
Решают самостоятельно задачу ,строят логические цепи рассуждений
|
ведут запись в тетради
|
осуществляют планирование, прогнозирование
контроль, коррекцию своих действий
|
ИНСТРУМЕНТАРИЙ ОЦЕНКИ СФОРМИРОВАННОСТИ
УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙТВИЙ
|
Задание
|
Деятельность учащегося *
|
Познавательная
|
Коммуникативная
|
Регулятивная
|
Сколько литров воды надо добавить к 20 литрам пятипроцентного раствора соли, чтобы получить 4-хпроцентный раствор?
В 30 кг пятипроцентного раствора соли добавили воды, при этом получили 1,5-процентный раствор соли. Сколько кг воды добавили?
|
Самостоятельно выделяет и формулирует познавательные цели.
Ищет и выделяет необходимую информацию.
Анализирует.
Самостоятельно выбирает эффективный способ решения задачи.
Выполняет знаково-символические действия.
Строит речевые высказывания в письменной форме.
Самостоятельно находит другие способы решения задачи. Анализирует результат.
|
Управляет своим поведением.
Владеет правилами вежливости.
|
Планирует свою деятельность в соответствии с поставленной задачей и условиями ее реализации.
Прогнозирует результат.
Самостоятельно находит несколько вариантов решения учебной задачи.
Вносит необходимые коррективы.
Самостоятельно осуществляет пошаговый и итоговый контроль
Адекватно воспринимает оценку своей деятельности учителем.
|
 Скачать 89.84 Kb.
Скачать 89.84 Kb.