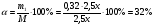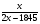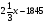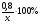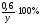Государственное бюджетное оздоровительное образовательное учреждение санаторного типа для детей, нуждающихся в длительном лечении
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
| Тема. Задачи на повышение концентрации. Задачи на понижение концентрации (тема 3). Форма проведения занятий: лекция, беседа, практикум по решению задач. Основная цель: сформировать умение работать с законами сохранения массы. В результате изучения темы учащиеся должны: - знать формулу содержания примеси основного вещества в смеси, алгебраические способы решения задач на смеси и сплавы; - понимать содержательный смысл понятий «концентрация вещества», «процентное содержание раствора»; - уметь составлять пропорции, находить неизвестные члены пропорции, выражать проценты в виде десятичной дроби и десятичные дроби в процентах, применять соответствующие понятия и формулы при решении задач на концентрацию смесей и сплавов. Использовать приобретенные умения и навыки в практической деятельности и повседневной жизни для - изменения концентрации растворов и смесей в быту, - приготовления смесей, растворов при строительстве, лепке, приготовлении красок в художественных мастерских, химических производствах. Ход урока
Вспомним, что такое процент и как найти долю числа. Если в задаче требовалось найти то или иное процентное содержание, то следует полученные доли перевести в процентные содержания. Практикум решения задач. Задача. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1.5% Решение. Для решения задачи применим табличный метод: Пусть требуется добавить x кг пресной воды. За чистое вещество примем соль. Тогда морская вода — это смесь с 5% -ным содержанием чистого вещества. Пресная вода — с 0%-ным содержанием чистого вещества. Переходя к долям, получаем, что - доля соли в морской воде составляет 0,05, -доля соли в пресной воде равна 0, -доля соли в смеси, которую нужно получить — 0,015. Происходит соединение смесей.
Исходя из третьей строки таблицы, составим уравнение m = 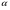 M : M : 0,05• 30 = 0,015(30 + x); 1,5 = 0,45 + 0,015x; 0,015 x = 1,5 — 0,45; 0,015x = 1,05; x = 70. Ответ: 70кг. Практикум решения задач с помощью изученных способов с последующим объяснением по группам. Задача. Имеется склянка 20%-го раствора кислоты и склянка 40% -го раствора кислоты. 1. группа. Смешали 200 г раствора кислоты из первой склянки и 300 г из второй. Определите массу кислоты и ее долю в полученном растворе. 2. группа. Из первой склянки взяли 300 г раствора кислоты. Сколько граммов раствора кислоты надо долить из второй склянки. Чтобы получить 32%-й раствор кислоты? 3. группа. Верно ли. Что если из второй склянки берут на 50% больше раствора кислоты, чем из первой, то полученная смесь является 32% - ым раствором кислоты? Решение: а) Заполним таблицу по условию задачи:
Масса кислоты в смеси: 0,2 • 200 + 0,4 • 300 = 40 +120 = 160 г. Процентное содержание кислоты в смеси рассчитаем по формуле 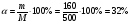 Ответ: 160 г, 32%. Ответ: 160 г, 32%.б) Пусть из второй склянки взяли x г раствора кислоты. Заполним таблицу:
Составим и решим уравнение: 600 + 0,4х = 0,32(300 + х), 0,08х = 36, откуда х=450. Ответ: 450 г. в) Пусть из первой склянки берут х г раствора. Заполним таблицу по условию задачи.
Рассчитаем содержание кислоты в смеси по формуле Задачи на понижение концентрации. 1 группа. Задача. Сироп содержит 18% сахара. Сколько килограммов воды нужно добавить к 40 кг сиропа. Чтобы содержание сахара составило 15%? Решение: Пусть надо добавить x кг воды. Заполним таблицу.
Так как масса сахара не изменилась. То составим и решим уравнение: 0,15(40 + x) = 7,2; 0,15• x = 1,2, откуда x = 8. Ответ: 8 кг. 2 группа. Задача. Сколько граммов воды нужно добавить к 5%-й йодной настойке массой 100 г, чтобы концентрация йода уменьшилось до 1% Решение: Способ 1. 1)100 · 0,05 = 5 г — масса йода в исходном растворе; 2)5 г — это 1% йода в полученном растворе. Масса полученного раствора составляет 100% и равна 500 г; 3) 500 — 100 = 400 г — столько воды надо добавить. Ответ: 400г. Способ 2. Пусть надо добавить x г воды. Заполним таблицу
Так как масса йода не изменилась, то составляем уравнение: 0,01(х + 100) = 5; 0,01х = 4; откуда х = 400 г. Ответ: 400 г. 3 группа. Задача. Сколько килограммов 5% - го раствора соли надо добавить к 15 кг 10%-го раствора той же соли, чтобы получить ее 8% - ный раствор? Решение: Пусть добавили х кг 5%-го раствора соли. Заполним таблицу.
Составим и решим уравнение: 1,5 + 0,05 х = 0,08(15 + х); 0,03х = 0.3; откуда х = 10. Ответ: 10 г. Задачи на повышение концентрации. 1 группа. Задача. Сплав меди с серебром содержит серебра на 1845 г больше чем меди. Если к нему добавить 1/3массы серебра, содержащего в сплаве, то получится новый сплав, содержащий 83,5% серебра. Какова масса сплава и процентное содержание серебра в нем? Решение: Пусть в сплаве содержится х г серебра. Заполним таблицу:
Составим уравнение: 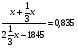 решая и находим, что х = 2505. решая и находим, что х = 2505. Масса сплава: 2· 2505 — 1845 = 3165 г. Процентное содержание серебра в сплаве: 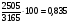 Ответ: 3165г, 79,1%. Ответ: 3165г, 79,1%.2 группа. Задача. Сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди? Решение: 45% - это 0,45. тогда 36 · 0,45 = 16.2 кг меди в сплаве. Пусть масса меди равна х кг, тогда (36 +х) кг — масса сплава после добавления. А масса меди в новом сплаве (16,2 +х) кг. Зная, что медь в новом сплаве составила 60%, то 16,2 +х = (36+х)·0,6. В результате х= 13,5 Ответ: 13.5 кг. 3 группа. Задача. Слили два раствора серной кислоты и получили смесь массой 10 кг. Определите массу каждого раствора, вошедшего в смесь. Если в первом растворе содержалось 800г серной кислоты, а во втором — 600 г. концентрация первого раствора была на 10% больше, чем концентрация второго раствора. Решение: заполним таблицу:
Составим систему уравнений 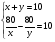 Решая и получим: х2 — 24х + 80 = 0 Решая и получим: х2 — 24х + 80 = 0х1 = 4; х2 = 20-не удовлетворяет условию задачи (х <10) Ответ: 4 кг и 6 кг. Итоги урока. Дом зад. Задачи из открытого банка задач ГИА и ЕГЭ. Приложение 6. Тема. Решение задач на «высушивание» или «задачи на сухое вещество» (тема 4). Форма проведения занятий: лекция, беседа, практикум по решению задач. Основная цель: сформировать умение решать задачи на высушивание. В результате изучения темы учащиеся должны: - знать формулу влажности, алгебраические способы решения задач на высушивание; - понимать, что означает процесс испарения и сушки, понятие «влажность»; - уметь составлять пропорции, находить неизвестные члены пропорции, выражать проценты в виде десятичной дроби и десятичные дроби в процентах, применять соответствующие понятия и формулы при решении задач на высушивание, решать задачи арифметическими и алгебраическими способами. Ход урока
Задачи на «высушивание». При решении этих задач надо объяснить, что все тела, вещества, продукты содержат в себе воду, которая частично испаряется. Поэтому при решении этих задач каждый раз разделяем данное нам вещество на воду и «сухой остаток», масса которого не меняется в условиях задачи. Вопрос. Где могут встречаться в жизни задачи на «высушивание»? Ответы. В практической деятельности и повседневной жизни для - определения необходимой массы ягод, грибов для сушки; -нахождение количества соли при выпаривании в пищевой промышленности; - определение влажности зерна лаборантам.
Для решения такого типа задач применим табличный метод. Рассмотрим задачи: Задача 1. Собрали 8 кг свежих цветов ромашки. Влажность которых 85% После того как цветки высушили, их влажность составила 20%. Чему равна масса цветков ромашки после сушки? Решение. Составим таблицу:
Значит, масса высушенных цветов равна 1.2 : 0.8 = 1.5 Ответ: 1,5. Задача 2. Имеется 0,5 т целлюлозной массы, содержащей 85% воды. После выпаривания получили массу, содержащую 25% целлюлозы. Сколько кг воды было выпарено? Решение: Пусть выпарили х кг воды. Заполним таблицу.
Составим и решим уравнение: 500 · 0,15 = (500 — х)0,25 0,25х =50, откуда х = 200. Ответ: 200г. Задача 3. Из 60% водного раствора спирта испарилась половина воды и 2/3 спирта. Какова процентное содержание спирта в получившемся растворе? Решение: 60% раствор спирта содержит 60% спирта и 100-60= 40% воды. Если масса раствора была х г, то спирта в нем было 0.6х г, а воды — 0,4х г. В результате испарения в растворе осталось:
Рассчитаем концентрацию получившегося раствора: 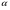 = m/ M = 0,2х/ 0,2х+0.2х = 1/2 = 50%. Ответ: 50%. = m/ M = 0,2х/ 0,2х+0.2х = 1/2 = 50%. Ответ: 50%. Задача 4. Для получения томат - пасты протертую массу томатов выпаривают в специальных машинах. Какова протертая масса томатов, содержащая 90% воды, если из нее получили 10 т томат – пасты, содержащей 30% воды? Решение табличным способом:
При выпаривании томатов испаряется вода, масса сухого вещества не меняется. Составляем уравнение: 0,1х = 0,7*10 0,1х = 7 х = 70 (т) – протертая масса томатов. Ответ: 70 т протертая масса томатов. Практикум решения задач. Задача. Собрали 8 кг свежих цветов ромашки. Влажность которых 85%. После того как цветки высушили, их влажность составила 20%. Чему равна масса цветков ромашки после сушки?
Значит, масса высушенных цветов равна 1.2 : 0.8 = 1.5 Ответ: 1,5. Задача. Имеется 0,5 т целлюлозной массы, содержащей 85% воды. После выпаривания получили массу, содержащую 25% целлюлозы. Сколько кг воды было выпарено? Решение: Пусть выпарили х кг воды. Заполним таблицу.
Составим и решим уравнение: 500 · 0,15 = (500 — х)0,25 0,25х =50, откуда х = 200. Ответ: 200г. Задача. Из 60% водного раствора спирта испарилась половина воды и 2/3 спирта. Каково процентное содержание спирта в получившемся растворе? Решение: 60% раствор спирта содержит 60% спирта и 100-60= 40% воды. Если масса раствора была х г, то спирта в нем было 0.6х г, а воды — 0,4х г. В результате испарения в растворе осталось:
Рассчитаем концентрацию получившегося раствора:  = m/ M = 0,2х/ 0,2х+0.2х = 1/2 = 50%. Ответ: 50%. = m/ M = 0,2х/ 0,2х+0.2х = 1/2 = 50%. Ответ: 50%.Итоги урока. Дом. зад. Решить задачи из открытого банка задач ГИА 2014г. Приложение 7. Задачи на переливание (тема 5). Форма проведения занятий: лекция, беседа, практикум по решению задач. Основная цель: сформировать умение решать задачи на переливание. В результате изучения темы учащиеся должны: - знать приемы и способы решения текстовых задач, - понимать, что при решении задач на переливание выполняются допущения: «закон сохранения масс» и «закон сохранения объемов», как для всей смеси, так и для каждого из ее компонентов; - уметь составлять уравнения и пропорции для решения задач на переливание, определять плотность раствора, решать задачи арифметическими и алгебраическими способами. Использовать приобретенные умения и навыки в практической деятельности и повседневной жизни для - решения задач на уроках химии, - выполнение производственных задач в химической, пищевой промышленности, быту. Ход урока. 1. Проверка дом. зад. 2. Лекция. При решении этих задач еще раз следует напомнить, что выполняются следующие допущения: «закон сохранения масс» и «закон сохранения объемов», как для всей семьи, так и для каждого из ее компонентов. При этом следует считать, что плотности растворов изменяются незначительно и примерно равны плотности воды, то есть растворы сильно разбавлены, или наоборот, имеем дело с сильно концентрированными растворами и разбавляем их незначительно, но тогда плотность раствора близка к плотности основного вещества. Для решения задач на переливание рассмотрим следующие задачи: Задача 1. В первой кастрюле был 1 л кофе. А во второй — 1 л молока. Из второй кастрюли в первую перелили 0,13 л молока и хорошо размешали. После этого из первой кастрюли во вторую перелили 0.13 л смеси. Чего больше: молока в кофе или кофе в молоке? Решение: 1) В первой кастрюле стало 1.13 л смеси, в которой молоко составило 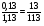 , а кофе , а кофе 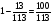
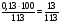 Ответ: одинаково. Задача 2. В сосуде объемом 10 л содержится 20% -й раствор соли. Из сосуда вылили 2 л раствора и долили 2 л воды. После чего раствор перемешали. Эту процедуру повторили ещё один раз. Определите концентрацию соли после первой и после второй процедуры. Решение: 1) Найдем начальную массу соли: m0 = 0,01 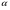 0 V = 0,2 · 10= 2 кг 0 V = 0,2 · 10= 2 кг2)После первой процедуры, соли осталось m1 = m0 - 0,01 · 2 = 2 - 0,2 · 2 = 1,6 кг. А ее концентрация после добавления 2 л воды стала равной 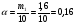 или 16% или 16%
m2 = m1 - 0,16 · 2 = 1.6 - 0,32 = 1,28 кг. После добавления воды концентрация стала 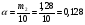 или 12,8% Ответ: 16%, 12,8% или 12,8% Ответ: 16%, 12,8% Рассмотрим задачу. В сосуде находится A г p% -го раствора соли. Из сосуда выливают a г раствора и наливают столько же литров воды, после чего раствор перемешивают. Эта процедура повторяется n раз . Какова доля соли после перемешиваний? Решение. Обратим внимание обучающихся на то, что объем раствора не меняется, а содержание соли и ее концентрация с каждым разом уменьшаются. Например, после первого переливания в сосуде останется соли 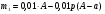 г гИ ее концентрация станет равной 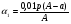 . .После второго переливания в сосуде останется соли 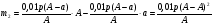 , ,Ее концентрация станет равной 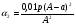 . .Аналогично рассуждая, получим, что после третьего переливания, масса оставшейся соли равна 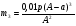 г, а ее концентрация г, а ее концентрация 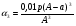 . Следовательно, после n переливаний масса соли станет равной . Следовательно, после n переливаний масса соли станет равной 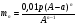 г., а ее концентрация г., а ее концентрация 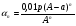 . .Ответ: 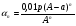 Запомним: 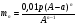 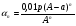 . Эти формулы будем применять для решения задач на переливание. . Эти формулы будем применять для решения задач на переливание.Задача. В сосуде находится A кг чистого спирта. Из него отливают a кг спирта и наливают a кг воды. После перемешивания получившейся смеси, с ней производят те же действия несколько раз. Сколько спирта останется в сосуде после n переливаний и какова будет доля спирта в получившейся смеси? Решение. Начальная концентрация спирта равна 100%, или 1. После первого переливания масса спирта будет равна 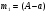 кг, а его концентрация равна кг, а его концентрация равна 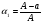 .после второго переливания .после второго переливания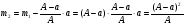 кг. кг.А концентрация 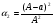 . .Аналогично рассуждая получаем после n-го переливания масса спирта будет равна 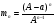 кг, а его концентрация кг, а его концентрация 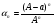 , или , или 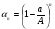 Ответ: 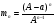 , , 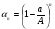 Закрепление темы, путем решения задач. Задача. Из сосуда емкостью 54 л, наполненного кислотой, вылили несколько литров кислоты и долили столько же литров воды, потом вылили столько же литров смеси. Тогда в смеси, оставшейся в сосуде, оказалось 24 л кислоты. Сколько литров кислоты вылили в первый раз? Решение. Пусть в первый раз вылили х л кислоты, тогда в сосуде осталось (54 - х) л кислоты, и после добавления воды 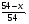 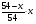 доля кислоты в растворе стала равна Во второй раз из доля кислоты в растворе стала равна Во второй раз из 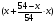 сосуда вылили х л смеси, в которых содержалось л сосуда вылили х л смеси, в которых содержалось л кислоты. Значит, за два раза вылили л, или 54-24=30 л кислоты. Составим и решим уравнение: 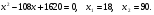 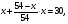 90 - не удовлетворяет условию задачи (90 > 54). Ответ: 18л. Задача. В сосуд емкостью 6л налито 4л 70% раствора серной кислоты. Во второй сосуд той же емкости налито 3л 90% раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нем получился 74% раствор серной кислоты? Найдите все допустимые значения процентного содержания раствора серной кислоты в 6л раствора в первом сосуде. Решение. Пусть х литров раствора кислоты нужно перелить из второго сосуда в первый. Тогда в нем станет (4 + х) литров 74 процентного раствора. 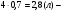 кислоты в первом сосуде. кислоты в первом сосуде.(0,9х) литров – кислоты нужно перелить. (2,8 + 0,9х) литров – кислоты в новом растворе. Учитывая, что новый раствор 74% и его объем (4 + х) литров, то кислоты в нем (0,74·(4 + х )) литров. Получим уравнение: 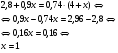 Найдем допустимые значения процентного содержания. Так как в первый сосуд налит 70 процентный раствор серной кислоты, а будем доливать 90 процентный раствор, то процентное содержание раствора будет увеличиваться. Из второго сосуда в первый можно перелить максимальное количество раствора кислоты – 2 литра. 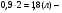 кислоты в двух литрах. кислоты в двух литрах.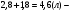 кислоты будет в первом сосуде. кислоты будет в первом сосуде.Тогда процентное содержание раствора серной кислоты в шести литрах раствора в первом сосуде может быть 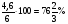 Ответ: Ответ: 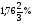 Рефлексия. Итоги урока. Дом. зад. Придумать задачи на переливание и решить их. Приложение 8. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||