Государственное бюджетное оздоровительное образовательное учреждение санаторного типа для детей, нуждающихся в длительном лечении
 Скачать 0.96 Mb.
|
              Государственное бюджетное оздоровительное образовательное учреждение санаторного типа для детей, нуждающихся в длительном лечении, «Болгарская санаторная школа-интернат»
Авторская программа элективного курса по математике «Решение задач на смеси, сплавы, концентрацию» Разработчик: учитель математики ГБООУ «Болгарская санаторная школа-интернат» Спасского муниципального района РТ Бондарева Людмила Николаевна Содержание.
Рабочая программа элективного курса «Решение задач на смеси, сплавы, концентрацию» составлена на основе:
Умение решать текстовые задачи является одним из основных показателей уровня сформированности математического образования, глубины освоения учебного материала. Поэтому любой экзамен, любой контроль знаний по математике содержит в качестве основной и, пожалуй, наиболее трудной части решение задач. За время обучения в школе решается огромное число задач. При этом решаются одни и те же задачи. И в итоге большая часть учеников овладевает общим умением решения задач, а встретившись с задачей незнакомого или малознакомого вида, теряются и не знают, как к ней подступиться. Для того, чтобы научиться решать задачи, надо много работать. Но эта работа не сводится лишь к решению большого числа задач. Если кратко обозначить то, что нужно сделать для этого, то можно сказать: надо научиться такому подходу к задаче, при котором задача выступает как объект тщательного изучения, а её решение – как объект конструирования и изобретения. Программа курса «Решение задач на смеси, сплавы, концентрацию» адресована обучающимся 9 классов, и рассчитана на 16 часов. Данный курс предназначен, в первую очередь, обучающимся, желающих расширить и углубить свои знания по математике, сделать правильный выбор профиля обучения в старших классах и качественно подготовиться к государственной (итоговой) аттестации. Разработка программы элективного курса обусловлена тем, что задачи с использованием таких понятий как концентрация, процентное содержание вещества в смеси, растворе, сплаве в школьном курсе математики практически отсутствуют, учащимся мало знаком алгоритм решения такого типа задач, что вызывает затруднения при решении текстовых задач на итоговой аттестации, математических олимпиадах, конкурсных работах. В последнее же время в контрольно-измерительные математике, проводящего в форме ЕГЭ и ГИА, включают и задачи на концентрацию, смеси и сплавы. Данный курс показывает связь математики с другими областями знаний, а также применение математических знаний к решению повседневно бытовых проблем человека, задач технологии производства, ориентирует учащихся на обучение по естественнонаучному, социально-экономическому профилю. Материал курса способствует формированию познавательной и социальной активности ученика. Цель курса: сформировать у учащихся умения и навыки решения задач на концентрацию, процентное содержание вещества в смеси, растворе, сплаве. Задачи курса:
2. Планируемые результаты. В результате изучения данного элективного курса учащиеся должны: Знать:
Уметь:
В ходе изучения курса обучающиеся повторяют: • Алгоритмы решения линейных уравнений. • Способы решения систем уравнений. • Виды текстовых задач и способы их решения. И дополнительно закрепляют умения: • Решать линейные уравнения, а также системы уравнений различными методами: подстановкой, сложением, введением новой переменной. • Определять тип текстовой задачи. • Составлять и решать математическую модель реальной ситуации. • Работать с математической моделью, в которой содержится несколько переменных, а также с моделью (системой), в которой число переменных превосходит число уравнений. • Применять полученные математические знания решения задач в повседневной жизни. • Использовать дополнительную литературу. Организация проведения аттестации учащихся. Итоговая аттестация по результатам изучения курса «Задачи на сплавы, смеси и концентрацию» предусмотрена с учетом самостоятельно выполненных работ учащимся (контрольная работа). Итоговая оценка предполагается накопительной, то есть результаты выполнения всех предложенных заданий оцениваются в баллах, которые суммируются по окончании изучения курса. Конкретные рамки по количеству баллов для получения той или иной оценки заранее не задаются, а оценка определяется по завершении изучения курса в зависимости от актуального уровня подготовки учащегося, его участия в проведении занятий. Оценка знаний и умений обучающихся 9 класса проводится в форме зачета по теме «Задачи на смеси, сплавы». В связи с тем, что за элективный курс оценки не выставляются, то можно предложить (по желанию обучающихся), что оценка за зачетную работу будет выставлена в журнале по предмету «математика» по пятибалльной системе. Возможные критерии оценок: Если обучающийся при сдаче зачета набрал 17 - 24 балла – учащийся блестяще освоил теоретический материал курса, получил навыки в его применении при решении конкретных математических задач, в работе над индивидуальными домашними заданиями ученик продемонстрировал умение работать с литературными источниками, он отличался активным участием при обсуждении решения задач, изучаемых в данном курсе; творческим подходом и большой заинтересованностью как при освоении курса в целом, так и при выполнении порученных ему учителем заданий. От 10 до 16 баллов – учащийся освоил идеи и методы данного курса в такой степени, что может справиться со стандартным заданием; ученик успешно сдал зачет и выполнял домашние задания, но без проявления явных творческих способностей. От 6 до 9 баллов – учащийся освоил наиболее простые идеи и методы курса, что позволило ему достаточно успешно выполнить такие задания. Менее 6 баллов – ученик не проявил ни прилежания, ни заинтересованности в освоении курса, он халатно отнесся к подготовке зачета и выполнению индивидуальных домашних заданий; он уклонялся от участия в обсуждение подходов решения задач. Текущий контроль уровня усвоения материала осуществляется по результатам выполнения учащимися самостоятельных, практических работ. Присутствует как качественная, так и количественная оценка деятельности. Качественная оценка базируется на анализе уровня мотивации учащихся, их общественном поведении, самостоятельности в организации учебного труда, а так же оценке уровня адаптации к предложенной жизненной ситуации (сдачи экзамена по алгебре в форме малого ЕГЭ). Количественная оценка предназначена для снабжения учащихся объективной информацией об овладении ими учебным материалом и производится по пятибалльной системе (по желанию обучающихся). Курс по теме «Задачи на смеси, сплавы и концентрацию» предполагает отработать целый блок текстовых задач, предлагаемых в рамках итоговой аттестации учащихся 9-х классов и в будущем сдачи ЕГЭ в 11-м классе и развитие умения учащихся самостоятельно решать текстовые задачи на смеси, сплавы и концентрацию. 3.Учебно-тематический план
4. Содержание программы. Тема 1: Начальные сведения из курса химии по теме «Массовая и объемная доли компонентов смеси (раствора)». Изучение основных понятий курса. Этапы решения задач. Составление таблицы данных задачи и её значение для составления математической модели. Способ решения задач «Пропорция». Тема 2: Общие подходы к решению задач на смеси, растворы и сплавы. Формула зависимости массы или объёма вещества в сплаве, смеси, растворе («часть») от концентрации («доля»), и массы или объёма сплава, смеси, раствора («всего»). Особенности выбора переменных и методики решения задач на сплавы, смеси, растворы. Тема 3: Задачи на растворы. Задачи на понижение, повышение концентрации. Конверт Пирсона. Тема 4: Задачи на «сухое вещество». Данная тема предполагает расширение знаний обучающихся о задачах на высыхание, усушку. Тема предполагает изучение общего алгоритма решения задач на «сухое вещество». Тема 5: Задачи на переливание. Выявление общей закономерности изменения той или иной величины в результате многократно повторяющейся операции. Задачи на разбавление. Тема 6: Задачи на смешивание растворов разных концентраций. Задачи на изменение концентрации растворов. Нахождение концентрации нового вещества. Применение различных способов решения задач. Тема 7: Задачи на сплавы различными способами. Данная тема предполагает углубление знаний о смесях, и сплавах, здесь не только рассматриваются задачи на переливание, смешение, но и решаются задачи жизненного характера (концентрация, усушка, переливание, задачи с экономическим и практическим содержанием). Рассматриваются решение задач с помощью схем и графиков. Тема 8: Зачет по теме. Итоговая письменная работа. Программа курса имеет практическую направленность. Задачи, используемые на занятиях, подобраны с учетом нарастания уровня сложности, их количество не создает учебных перегрузок для школьников. Содержание программы способствует интеллектуальному, творческому, эмоциональному развитию школьников; предусматривает формирование устойчивого интереса к предмету, развитие и выявление математических способностей, ориентацию на профессии, связанные с математикой, выбор дальнейшего профиля.
14. Цыганов Ш. И. Все задачи ЕГЭ по математике прошлых лет: Учебное пособие / Ш. И. Цыганов – 4-е изд., дополненное – Уфа: Центр педагогических измерений, 2008-324с. Литература для обучающихся
Приложение 1. Тема. «Начальные сведения из курса химии по теме «Массовая и объемная доли компонентов смеси (раствора)» (тема1). Форма проведения занятий: лекция, практикум по решению задач. Основная цель: изучить табличный способ решения задач и способ «пропорция». В результате изучения темы учащиеся должны:
- понимать содержательный смысл терминов «процент», «смесь» как специального способа выражения доли величины;
Использовать приобретенные умения и навыки в практической деятельности и повседневной жизни для: - процентных вычислений людям различных профессий - решения математических, химических, задач школьнику и студенту. Ход урока Лекция. Учитель. Сегодня мы рассмотрим методику решения задач на смеси, растворы и сплавы. Но первым делом необходимо повторить такие понятия, как: 1. Концентрация (доля чистого вещества в смеси (сплаве)); 2. Масса смеси (сплава); 3. Масса чистого вещества в смеси (сплаве). А также то, что процентом называется его сотая часть и три основные задачи на проценты: 1. Найти 15% от числа 60. Решение:60•0,15=9. 2. Найти число, 12% которого равны 30 . Решение: 30:0,12=250. 3. Сколько процентов составляет число 120 от 600? Решение: 120:600•100%=20%. Имеются различные типы задач на смеси и сплавы. Это:
Сообщается, что известно уже учащимся из курса химии 8 класса о том, что такое массовая доля вещества, ее обозначение, формула, в чем ее выражают. Эта величина может быть выражена либо в долях единицы, либо в процентах. Прежде всего, введем основные понятия. Говоря о смесях, растворах и сплавах, будем употреблять термин «смесь» независимо от ее вида (твердая, жидкая, газообразная, сыпучая и т. д.). Смесь состоит из «чистого вещества» и «примеси». Что есть «чистое вещество», определяется в каждой задаче отдельно, однако при этом все остальные вещества, составляющие смесь, относят к примеси. Необходимо помнить, что долей ( 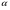 ) чистого вещества в смеси называется отношение количества чистого вещества (m) в смеси к общему количеству (M) смеси при условии, что они измерены одной и той же единицей массы или объема: 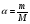 Понятие доли чистого вещества в смеси можно вводить следующей условной записью: Количество чистого вещества в смеси Доля чистого вещества в смеси = Общее количество смеси Процентным содержанием чистого вещества в смеси (с) называют его долю, выраженную процентным отношением: 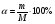 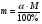 При решении задач следует руководствоваться тем, что при соединении (разъединении) смесей с одним и тем же чистым веществом количества чистого вещества и общее количества смесей складываются (вычитаются). Основные этапы решения задач. 1. Выбор неизвестной (или неизвестных). В качестве неизвестных величин выбирают те, которые требуется найти. Но иногда целесообразно обозначать неизвестными некоторые промежуточные величины, через которые легко выражаются искомые. 2. Выбор чистого вещества. Из веществ, фигурирующих в условии задачи, выбирается одно в качестве чистого вещества. Чаще всего выбирают вещество, о котором идет речь в требовании задачи, или вещество, о доле которого в условии содержится больше всего информации. 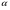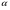При этом, если - доля чистого вещества, то (1 - ) - доля примеси.3. Переход к долям. Если в задаче имеются процентные содержания. Их следует перевести в доли и в дальнейшем работать только с долями. 4. Отслеживание состояния смеси. На каждом этапе изменения смеси (добавление, изъятие) необходимо описывать состояние смеси с помощью трех основных величин m, M, 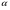.5. Составление уравнения. В результате преобразований смеси, описанных в задаче, мы приходим к ее итоговому состоянию. Оно характеризуется величинами m,M, 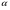, содержащими неизвестные. 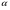Уравнением, связывающим эти неизвестные, будет уравнение m = M.В ходе осуществления этих этапов строим таблицу.
Решение уравнения (или их системы) и нахождение требуемых величин. Рассмотрим задачу. Задача. Определите в каких пропорциях нужно смешать а%-й и b%-й растворы кислоты (a < b), чтобы получить с%-й раствор. Решение. Решение задачи с помощью таблицы. Возьмем х грамм а%-го раствора и у грамм b%-го раствора кислоты. Составим таблицу:
Составим и решим уравнение: 0,01ах + 0,01by = 0,01c(x + y), (b – с)у = (с – а)х, x : у = (b – с) : (с – а). Теперь рассмотрим конкретную задачу. Задача. При смешивании 5%-го и 40%-го растворов кислоты получили 140 г 30% -го раствора кислоты. Сколько граммов каждого раствора было взято? Решение: Пусть взяли х г 5%-го раствора кислоты. Заполним таблицу.
Составим уравнение: 0,05х + 0.4(140 — х) = 0,3 · 140; 0.35х = 14; х = 40. Ответ: 40 г 5% -го и 100г 40%-го. Закрепление темы, путем решения задач. Я предлагаю вам рассмотреть задачу следующего содержания, которая предлагалась при сдаче ЕГЭ по математике. Задача. Один раствор содержит 55% азотной кислоты, а второй 30%. Сколько нужно взять первого и второго растворов, чтобы получить 100 кг 50% -ного раствора азотной кислоты? (Учащиеся самостоятельно решают задачу с помощью уравнения с последующей проверкой у доски).
На основании того, что массовая доля растворённого вещества нового раствора равна сумме массовых частей растворённого вещества первого и второго растворов можно составить уравнение: 0,55х+0,3(100-х)=0,5* 100 0,55х+30-0,3х=50 0,25х=50-30 0,25х=20 х=80 Значит, масса 55%-го раствора 80кг, масса 30%-го раствора 100-80=20(кг) Ответ: 80кг; 20кг. Физкультминутка. Давайте рассмотрим еще способ решения задач на смеси и концентрацию . Способ «Пропорция». Задача. Смешивают 300г 90% раствора соли и 900 г 30% раствора той же соли. Найти содержание соли в полученном растворе? Решение:
90% х г 30% х
III. 100% 1200 x 540 4) 540· 100 : 1200 = 45%. Ответ: 45%. Задачи на закрепление изученного материала. Решение задачи у доски Задача. Какой концентрации получится раствор при смешивании 300 г 50% раствора соли и раствора в котором 120 г соли составляют 60%?
50% х 60% 120г
3) 300 + 200 = 500 г. 4) 150 + 120 = 270 г. III. 100% 500 х 270г 5) 270 · 100 : 500 = 54%. Ответ: 54%. Самостоятельное решение с последующей проверкой Задача. 5 л сливок с содержанием жира 5% смешали с 4 л. 20% сливок и к смеси добавили 1 л. чистой воды. Какой жирности получилась смесь? Итоги урока. Что нового и полезного вы сегодня узнали на уроке? Дом зад. Найти задачи из прошлых лет ГИА или ЕГЭ и решить их. Приложение 2. |