Государственное бюджетное оздоровительное образовательное учреждение санаторного типа для детей, нуждающихся в длительном лечении
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
| Тема. Общие подходы к решению задач на смеси, растворы и сплавы. Решение задач на смеси и сплавы с помощью уравнения (тема 2). Цели урока: Научиться решать задачи на сплавы, растворы и смеси с помощью уравнения. Воспитывать интерес к предмету через межпредметные связи с химией, обращая внимание на аккуратность, дисциплинированность и самостоятельность. Развивать устную и письменную речь, внимание и логическое мышление. Ход урока Вводная беседа. Учитель. Задачи на смеси и сплавы вызывают наибольшие затруднения. В процессе решения каждой такой задачи целесообразно действовать по следующему алгоритму: Алгоритм решения задачи на сплавы, растворы и смеси: 1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи. 2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами. 3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели. 4. Изучение полученного решения, критический анализ результата. Очень часто в задачах на смеси и сплавы используются понятия объемной концентрации и массовой концентрации компонентов, составляющих раствор или сплав. Например, если имеется 40%-ный раствор соли, то в этом растворе 0,4 объема занимает <чистая> соль. Значит, объемная концентрация соли в растворе равна 0,4. Если сплав содержит свинец и медь в отношении 4 : 7, то 4 :11 массы всего этого сплава составляет свинец, а 7 :11 - медь, т. е., массовые концентрации свинца и меди в сплаве соответственно равны 4 : 11 и 7 : 11. . Решение задач с помощью уравнения. Примечание: в задачах на смешивание важно помнить, что вес или объем одного и того же вещества накапливается суммированием его веса по всем смешивающимся смесям. Обычно такие задачи решаются с введением двух переменных, каждая для своего начального сплава (смеси). Учитель объясняет решение задачи. Задача. Сколько надо взять 5 процентного и 25 процентного раствора кислоты, чтобы получить 4 л 10 процентного раствора кислоты? Решение. 0,1· 4=0,4(л) – кислоты в новом растворе. Пусть х л надо взять первого раствора. Тогда второго – (4 – х) л, а количество получившегося раствора 2х. 0,05х л – кислоты в первом растворе. 0,25· (4 – х) л – кислоты во втором растворе. 0,05х + 0,25· (4 – х) = 0.05х + 1 – 0,25х = (1 – 0,2х) л. Получим уравнение 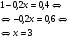 3 л надо взять первого раствора. 4 – 3 = 1 л – второго. Ответ: 1 л, 3 л Решение у доски. Задача. Даны 70% и 10% растворы. Сколько нужно взять каждого из этих растворов, чтобы получилось 600 граммов 30% раствора? x- кол-во взятого 70% раствора 600-x – кол-во взятого 10% раствора 70%= 0,7; 10%= 0,1; 30%= 0,3 0,7x + 0,1*(600-х) = 0,3*600 0,7х + 60 – 0,1х = 180 0,6х -120 = 0 0,6х = 120 x = 200 600-200=400гр Ответ: чтобы получилось 600 гр 30% раствора, нужно взять 200гр 70% раствора и 400гр 10% раствора. Задача. Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. Решение. Условно разделим сплав на медь и еще какой-то металл. Пусть х кг масса первого сплава. Тогда масса второго сплава (х + 3) кг, а масса третьего сплава (х + (х + 3)) = (2х + 3) кг. Масса меди в первом сплаве (0,1х) кг, во втором – (0,4·(х + 3)) кг, а в третьем – (0,3· (2х +3)) кг. Получим уравнение: 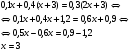 3 кг масса первого сплава. 2 · 3 + 3 = 9 (кг) – масса третьего сплава. Ответ: 9 кг. Итоги урока. Дом. зад. Найти задачи из открытого банка задач ГИА и ЕГЭ и решить их. Приложение 3. Тема. Задачи на растворы. Правило «креста» (тема 3). Форма проведения занятий: лекция, беседа, практикум по решению задач. Основная цель: рассмотреть различные способы решения задач на смеси и сплавы. В результате изучения темы учащиеся должны: - знать способы решения задач на смеси и сплавы: с помощью уравнения, системы уравнений, по правилу «креста»; - понимать содержательный смысл терминов «смесь», «сплав»; - уметь записывать условие задачи на смеси и сплавы в виде таблицы, решать линейные уравнения и системы линейных уравнений, задачи на смеси и сплавы. Использовать приобретенные умения и навыки в практической деятельности и повседневной жизни для - решения задач на уроках химии; - получения растворов и смесей в медицине, кулинарии, консервировании, при приготовлении пищи. Ход урока. Практикум решения задач. Изучение нового способа «Правило креста» При решении задач на смешивание растворов разных концентраций используется «правило креста». В точке пересечения двух прямых обозначают концентрацию смеси. У концов этих прямых слева от точки пересечения указывают концентрации составных частей смеси, а справа – разности концентраций смеси и ее составных частей: При решении задач на смешивание растворов разных концентраций автор использует диагональные схемы («правило креста»). На диагональной схеме в точке пересечения двух прямых обозначают концентрацию смеси. Например, далее в задаче 2 – это 80%. У концов этих прямых слева от точки пересечения указывают концентрации составных частей смеси, а справа – разности концентраций смеси и ее составных частей: 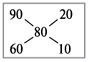 Из этой схемы следует, что, например, для приготовления 30 г 80%-го раствора H3PO4 требуется взять 20 г 90%-го и 10 г 60%-го растворов кислоты. Например, для приготовления 30 г 80%-го раствора H3PO4 требуется взять 20 г 90%-го и 10 г 60%-го растворов кислоты. Практикум решения задач. Старинный способ решения задач на смешивание двух веществ (метод рыбки) Задача. У некоторого человека были на продажу масла двух сортов: одно ценою 10 гривен за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла ценою 7 гривен? 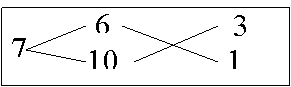 Из схемы делаем заключение, что дешевого масла нужно взять втрое больше, чем дорогого, т.е. для получения одного ведра ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого масла 3/4. Задача. Торговец продает орехи двух сортов: грецкие по 450 рублей за килограмм и миндаль по 540 рублей за килограмм. Мама решила купить смесь орехов за 500 рублей. В какой пропорции торговцу надо смешать орехи, чтобы получить эту смесь? Решение: метод «рыбки» 450 руб. 540 – 500 = 40 500 руб. 540 руб. 500 – 450 = 50 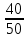 = = 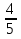 Ответ: 4 части ореха первого сорта и 5 частей ореха второго сорта надо смешать торговцу, чтобы поучить эту смесь. Способ Л.Ф. Магницкого для трех веществ Задача. Некто имеет чай трех сортов – цейлонский по 5 гривен за фунт, индийский по 8 гривен за фунт и китайский по 12 гривен за фунт. В каких долях нужно смешать эти сорта, чтобы получить чай стоимостью 6 гривен за фунт? 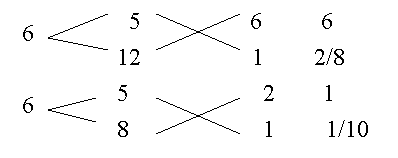 Взять 6+2=8 частей чая ценой по 5 гривен и по одной части ценой 8 гривен и 12 гривен за один фунт. Возьмем 8/10 фунта чая ценой по 5 гривен за фунт и по1/10 фунта чая ценой 8 и 12 гривен за фунт, то получим 1 фунт чая ценой 8/10*5 + 1/10*8 + 1/10*12 = 6 гривен Задача. Сплавили два слитка серебра: 75 г 600-й и 150 г 864-й пробы. Определить пробу сплава. Пусть проба сплава равна х. Составим диагональную схему: 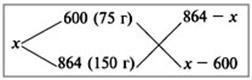 Получаем: (864 – х): (х – 600) = 75: 150 1728 – 2х = х – 600 х = 776. Ответ: сплав 776-й пробы. Задача. Латунь – сплав меди и цинка. Кусок латуни содержит меди на 11 кг больше, чем цинка. Этот кусок латуни сплавили с 12 кг меди и получили латунь, в котором 75% меди. Сколько килограммов меди было в куске латуни первоначально? Решение. Обозначим искомую величину за х. Тогда масса первоначального куска латуни 2х – 11, а его содержание меди составляет процентов. Поскольку «медность» куска меди 100%, то по правилу креста получаем: 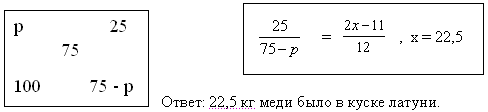 Задача (самостоятельно). В бидон налили 4л молока трехпроцентной жирности и 6л молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне? Итоги урока. Домашнее задание: К каждой задаче составить по одной обратной и решить с помощью «правила креста» любую задачу на ваш выбор.. 1. Один раствор содержит 55% азотной кислоты, а второй 30%. Сколько нужно взять первого и второго растворов, чтобы получить 100кг 50%-ного раствора азотной кислоты? 2. К 15 г 10% раствора соли добавили 5% раствор соли и получили 8% раствор. Какое количество граммов 5% раствора добавили? 3. Морская вода содержит 5% (по массе) соли. К 40кг морской воды добавили пресной воды и содержание соли в полученной воде составило 2%. Чему равна масса добавленной воды? 4. Сколько воды нужно добавить к 250г раствора соли для понижения его процентной концентрации с 45% до 10%? 5. Необходимо приготовить из безводной фосфорной кислоты 85%-ную фосфорную кислоту. В каких отношениях( по массе) следует смешать безводную кислоту с водой? Приложение 4. Тема. Основные способы решения задач на смешивание растворов разных концентраций. Конверт Пирсона (тема 3). «Только из союза двоих, работающих вместе и при помощи друг друга ,рождаются великие вещи.» Антуан Де Сент-Экзюпери Цели урока: 1. Продолжить работать над алгебраическим способом решения задач на смешивание растворов и применять математический аппарат при решении задач химического содержания. 2. Развивать у обучающихся желания и потребности обобщения изучаемых факторов. 3. Способствовать развитию творческого мышления, самостоятельности и творчества при изучении данной темы. Ход урока. 1. Орг. момент. Учитель. Сегодня на уроке мы продолжим работать над задачами на смешивание растворов алгебраическим методом и рассмотрим новый способ решения этих задач под названием «Конверт Пирсона», который позволяет рационально распределить время при решении задач на растворы. В последнее время в учебниках по математике, начиная с 5-го класса появилось много задач химического содержания на растворы, поэтому поняв химическую сущность задачи и применив математический аппарат, можно быстро справиться с задачей, тем более, что вы владеете некоторой химической терминологией, благодаря предмету «Введение в химию», который вы начали изучать в этом году. Начать сегодняшний урок я бы хотела замечательными словами: «Только из союза двоих, работающих вместе и при помощи друг друга рождаются великие вещи». 2. Актуализация знаний. Вспомним основные моменты, которые нам понадобятся на уроке. Работаем устно: 1. В чём заключается основное свойство пропорции? 2. Как найти неизвестный средний член пропорции? 3. Как найти неизвестный крайний член пропорции? 4. Из каких компонентов состоит раствор? 5. Из чего складывается масса раствора? 6. Что называется массовой долей растворённого вещества? 7. В чём измеряется массовая доля растворённого вещества? 8. Когда массовая доля растворённого вещества измеряется в процентах? 9. Что показывает массовая доля растворённого вещества? 10. 48% раствор. Что это значит? 11. Сколько г соли содержится в 250г 20%-го раствора? 12. 15г соли растворили в 10г жидкости. Определить процентную концентрацию раствора. 3. Изучение нового материала. Учитель: Открыли тетради, записали сегодняшнее число, тему урока: «Решение задач на смешивание растворов. Конверт Пирсона». Учитель: А теперь представим себе, что мы учимся в 11-м классе и очень скоро нам сдавать ЕГЭ. Оказывается, эту задачу можно решить намного проще с помощью нового метода - метод «креста».. При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора. Пусть требуется приготовить раствор определенной концентрации. В распоряжении имеется два раствора с более высокой и менее высокой концентрацией, чем нужно. Если обозначить массу первого раствора через 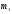 , а второго – через , а второго – через 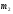 , то при смешивании общая масса смеси будет складываться из суммы этих масс. , то при смешивании общая масса смеси будет складываться из суммы этих масс.Пусть массовая доля растворённого вещества в первом растворе – 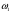 , во втором – , во втором – 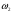 , а в их смеси – , а в их смеси – 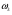 . Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах: . Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах: 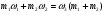 , , 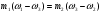 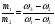 Очевидно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворённого вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси. ω1 ω3 — ω2 ω3 ω2 ω1 — ω3 При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения (метод креста) или квадрат Пирсона. Разберем этот метод на примере решения задачи. Задача. Один раствор содержит 20% соли. А второй — 70%. Сколько граммов первого и второго растворов нужно взять. Чтобы получить 100 г 50% -го солевого раствора? Решение: Решим задачу по правилу «креста». Составим схему. 20 20 50 70 30 Значит, 10 г смеси составляют 50 частей. Одна часть — 100 :(30 + 20) = 2 г, 70-ый раствор - 2· 30 = 60 г., а 20% раствор – 2 · 20 = 40 г. Ответ: 20%-40 г, 70% — 60 г. Теперь решите самостоятельно. Задача. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%? Решение: 5% 1,5% 30 кг 1,5% 0% 3,5% х кг 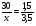 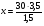 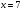 Конверт Пирсона в квадрате! Сегодня мы рассмотрим еще один оригинальный способ решения задач на концентрацию и решим одну из них разными способами. Итак… Условие задачи: Даны 70% и 10% растворы. Сколько нужно взять каждого из этих растворов, чтобы получилось 600 грамм 30% раствора. Сначала решим задачу способом, который известен всем нам, то есть алгебраическим. За величину Х возьмем количество взятого 70% раствора, следовательно, 600-Х – количество взятого 10% раствора. Как мы знаем, 70%=0,7, 10%=0,1, а 30%=0,3. Составим уравнение, находим Х. Х = 200 грамм, это количество 70% раствора, следовательно, 600-Х=600-200=400 граммов 10% раствора. Сейчас мы познакомим вас с более удобным и оригинальным способом решения этой задачи, который носит название «конверт Пирсона» в квадрате. Этот способ предложил английский математик и статистик Карл Пирсон. Мы имеем 70% раствор, 10% раствор. Нужно получить 600 грамм 30% раствора.
Из 30 вычитаем 10, в правый верхний угол записываем 20. Из 70 вычитаем 30, в правый нижний угол записываем 40. Складываем получившиеся результаты и записываем во вторую строку справа. 40+20=60. Количество раствора делим на последний результат, т.е. 600/60=10. 10 умножаем на 20 и 40, получаем ответ, 400 и 200 грамм. Немного истории и любопытных фактов. (Сообщение готовит обучающийся как дополнительное дом. зад.) А теперь немного о Пирсоне…Карл Пирсон родился 27 марта в 1857 году в Лондоне. Он был разносторонним человеком, активно изучал историю, математику, статистику и германистику. Большую часть 80-х годов XIX века он провел в Берлине, Гейдельберге, Вене и Брикслеге. Интересовали его религия и поэзия – с одинаковым интересом он изучал Гёте и Священное Писание. Занимали Пирсона и вопросы пола – он даже основал Клуб Мужчин и Женщин. В 1898 году получил медаль Дарвина. Карл Пирсон Погиб в Англии в городе Суррее 27 апреля 1936 года. Прожил он 79 лет. Как и все методы решений, конверт Пирсона имеет свои преимущества и недостатки. Одним из преимуществ этого способа является то, что он доступен ученикам, которые не умеют решать уравнения. Также квадрат Пирсона очень полезен для домохозяек, чтобы получать нужную концентрацию уксуса или сиропа. Недостатком этого метода является то, что его можно применять только при смешивании двух растворов. То есть если нужно смешать три или более веществ, конверт Пирсона здесь не поможет. Учитель. Итак, сделаем вывод: Для решения задач на проценты существует оригинальный метод решения «Конверт Пирсона». Он удобен для домохозяек, доступен ученикам, которые не умеют решать уравнения, но этот способ нельзя применять при смешивании трех и более растворов. А теперь с помощью квадрата Пирсона решим задачи по 2 вариантам. 1 вариант. Задача. Сколько граммов воды нужно добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20% ? Сколько граммов 20% сиропа получится?
180 : 20 = 9 Х = 9 * 25 =225гр Ответ: 45г., 225г. 2 вариант. Задача. Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла из этих сортов, чтобы получить 140 тонн стали, содержащей 30% никеля? 140 : 35 = 4
140 : 35 = 4 Ответ: 40т, 100т. Решите самостоятельно с последующей проверкой: Задача. К 25% раствору добавили 6 литров соли, и он стал 40%. Сколько соли надо добавить, что бы получить 50%-ный раствор соли. Учитель: Составьте, пожалуйста, задачу, обратную данной. (Ученики предлагают свои варианты задач) Учитель останавливается на одной из задач и предлагает её решить с помощью «конверта Пирсона». Обратная задача. Смешали 80кг 55%-го раствора азотной кислоты и 20кг 30%-го раствора. Найти процентную концентрацию полученного раствора. Ответ: 50%. Итоги урока. Рефлексия. Учитель: Итак, сегодня на уроке мы познакомились ещё с одним способом решения задач на смешивание растворов. Я хотела бы услышать от вас ответ на следующие вопросы: 1. Нужен ли нам данный способ и что в нём замечательного? 2. А нужен ли нам алгебраический способ? После того, как учитель выслушал ответы учеников, делает вывод: Алгебраический способ решения задач на смешивание растворов учит детей строить цепочку логических рассуждений. «Конверт Пирсона» - это механический способ, который позволяет рационально и экономно проводить вычисления при решении задач по алгебре. Поэтому, зная, два способа решения задач на растворы, один из них всегда можно применить в нужной ситуации. Дом зад. Придумать самим задачи и решить их с помощью изученных способов. Приложение 5. |