Государственное бюджетное оздоровительное образовательное учреждение санаторного типа для детей, нуждающихся в длительном лечении
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
| Тема. Задачи на смешивание растворов разных концентраций Решение задач с помощью систем уравнений (тема 6). Форма проведения занятий: беседа, практикум по решению задач. Основная цель: сформировать умение решать задачи на смешивание. В результате изучения темы учащиеся должны: - знать алгебраические способы решения задач на смеси и сплавы; - понимать, что означают термины «концентрация», «смесь»; - уметь определять тип задачи, - решать задачи арифметическими и алгебраическими способами. Использовать приобретенные умения и навыки в практической деятельности и повседневной жизни для определения концентрации растворов в пищевой промышленности, на уроках химии, в быту. Ход урока Вводная беседа Учитель. Ребята, как вы думаете, что такое «концентрация», «смесь» Ответы детей. Учитель. На прошлых уроках мы решали задачи на составление уравнений с одной неизвестной. Сегодня мы будем решать задачи с помощью систем уравнений с двумя неизвестными. Например, рассмотрим задачу. Задача 1. Имеется два сплава. Первый содержит 10% никеля, второй- 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Решение. Условно разделим сплав на никель и еще какой-то металл. Пусть х кг масса первого сплава, у кг – второго. Так как масса третьего сплава 200 кг, то получим уравнение 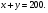 Масса никеля в первом сплаве (0,1х) кг, во втором – (0,3у) кг, а в новом - 200·0,25=50 кг. Получим второе уравнение 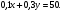 Получим систему уравнений: 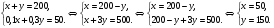 50 кг – масса первого сплава. 150 кг – масса второго сплава. 150 – 50 = 100 (кг) Ответ: на 100 кг. Работа в группах с последующим обсуждением каждой группы. 1 группа. Задача. При смешивании 30 процентного раствора серной кислоты с10 процентным раствором серной кислоты получилось 400 г 15 процентного раствора. Сколько граммов 30 процентного раствора было взято? Решение. Пусть х г масса 30 процентного раствора серной кислоты, а у г – 10 процентного. Получим уравнение х + у = 400. 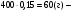 кислоты в новом растворе. кислоты в новом растворе.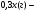 кислоты в первом растворе. кислоты в первом растворе.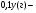 кислоты во втором растворе. кислоты во втором растворе.Получим второе уравнение 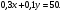 Получим систему уравнений: 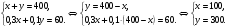 100 г 30 процентного раствора было взято. Ответ:100 г. 2 группа. Задача. Имеются два слитка сплава серебра и олова. Первый слиток содержит 360г серебра и 40г олова, а второй слиток – 450г серебра и 150г олова. От каждого слитка взяли по куску, сплавили их и получили 200г сплава, в котором оказалось 81% серебра. Определите массу (в граммах) куска, взятого от второго слитка. Решение. Первый слиток имеет вес 400 г, второй – 600 г. 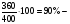 серебра в первом слитке (соответственно и в первом куске). серебра в первом слитке (соответственно и в первом куске).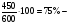 серебра во втором слитке (соответственно и во втором куске). серебра во втором слитке (соответственно и во втором куске).Пусть х г масса куска, взятого от первого слитка, а у г – от второго. 0,9х (г) – серебра в первом куске; 0,75у (г) – серебра во втором куске; 200 · 0,81 = 162 (г) – серебра в новом сплаве. Получим систему уравнений: 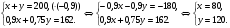 120 г нужно взять от второго слитка. Ответ: 120 г. 3 группа. Задача. Первый раствор содержит 40% кислоты, а второй - 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 процентного раствора, то получился бы 70 процентный раствор. Сколько литров 60 процентного раствора кислоты было первоначально? Решение. Пусть х л было 40 процентного, а у л – 60 процентного. Тогда нового, 20 процентного раствора – (х + у + 5) л. 0,4х (л) – кислоты в первом растворе; 0,6у (л) – кислоты во втором растворе; 0,2·(х + у + 5) (л) – кислоты в новом растворе. Получим уравнение 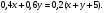 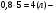 кислоты в 80 процентном растворе; кислоты в 80 процентном растворе;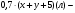 кислоты в новом, 70 процентном растворе. кислоты в новом, 70 процентном растворе.Получим второе уравнение 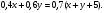 Получим систему уравнений: 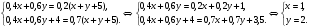 2 л 60 процентного раствора было первоначально. Ответ: 2 л. Рефлексия. Итоги урока. Дом зад. Задача. Смешали 30% и 10% растворы соляной кислоты и получили 600 г 15% раствора. Сколько граммов каждого раствора было взято? Приложение 9. Тема. Задачи на смешивание растворов разных концентраций. Решение задач с помощью систем уравнений (тема 6). Форма проведения занятий: лекция, беседа, практикум по решению задач. Основная цель: сформировать умение решать задачи на смешивание. В результате изучения темы учащиеся должны: - знать алгебраические способы решения задач на смеси и сплавы; - понимать, что означают термины «концентрация», «смесь»; - уметь определять тип задачи , - решать задачи арифметическими и алгебраическими способами. Использовать приобретенные умения и навыки в практической деятельности и повседневной жизни для определения концентрации растворов в пищевой промышленности, на уроках химии, в быту. Ход урока Вводная беседа Учитель. Ребята, как вы думаете, что такое «концентрация», «смесь» Ответы детей. Учитель. На прошлых уроках мы решали задачи на составление уравнений с одной неизвестной. Сегодня мы будем решать задачи с помощью систем уравнений с двумя неизвестными. Например, рассмотрим задачу. Задача 1. Имеется два сплава. Первый содержит 10% никеля, второй- 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Решение. Условно разделим сплав на никель и еще какой-то металл. Пусть х кг масса первого сплава, у кг – второго. Так как масса третьего сплава 200 кг, то получим уравнение 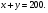 Масса никеля в первом сплаве (0,1х) кг, во втором – (0,3у) кг, а в новом - 200·0,25=50 кг. Получим второе уравнение 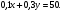 Получим систему уравнений: 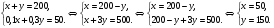 50 кг – масса первого сплава. 150 кг – масса второго сплава. 150 – 50 = 100 (кг) Ответ: на 100 кг. Работа в группах с последующим обсуждением каждой группы. 1 группа. Задача. При смешивании 30 процентного раствора серной кислоты с10 процентным раствором серной кислоты получилось 400 г 15 процентного раствора. Сколько граммов 30 процентного раствора было взято? Пусть х г масса 30 процентного раствора серной кислоты, а у г – 10 процентного. Получим уравнение х + у = 400. 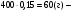 кислоты в новом растворе. кислоты в новом растворе.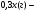 кислоты в первом растворе. кислоты в первом растворе.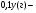 кислоты во втором растворе. кислоты во втором растворе.Получим второе уравнение 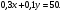 Получим систему уравнений: 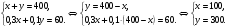 100 г 30 процентного раствора было взято. Ответ:100 г. 2 группа. Задача. Имеются два слитка сплава серебра и олова. Первый слиток содержит 360г серебра и 40г олова, а второй слиток – 450г серебра и 150г олова. От каждого слитка взяли по куску, сплавили их и получили 200г сплава, в котором оказалось 81% серебра. Определите массу (в граммах) куска, взятого от второго слитка. Первый слиток имеет вес 400 г, второй – 600 г. 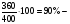 серебра в первом слитке (соответственно и в первом куске). серебра в первом слитке (соответственно и в первом куске).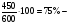 серебра во втором слитке (соответственно и во втором куске). серебра во втором слитке (соответственно и во втором куске).Пусть х г масса куска, взятого от первого слитка, а у г – от второго. 0,9х (г) – серебра в первом куске; 0,75у (г) – серебра во втором куске; 200 · 0,81 = 162 (г) – серебра в новом сплаве. Получим систему уравнений: 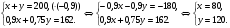 120 г нужно взять от второго слитка. Ответ: 120 г. 3 группа. Задача. Первый раствор содержит 40% кислоты, а второй - 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 процентного раствора, то получился бы 70 процентный раствор. Сколько литров 60 процентного раствора кислоты было первоначально? Пусть х л было 40 процентного, а у л – 60 процентного. Тогда нового, 20 процентного раствора – (х + у + 5) л. 0,4х (л) – кислоты в первом растворе; 0,6у (л) – кислоты во втором растворе; 0,2·(х + у + 5) (л) – кислоты в новом растворе. Получим уравнение 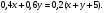 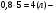 кислоты в 80 процентном растворе; кислоты в 80 процентном растворе;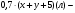 кислоты в новом, 70 процентном растворе. кислоты в новом, 70 процентном растворе.Получим второе уравнение 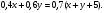 Получим систему уравнений: 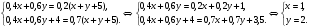 2 л 60 процентного раствора было первоначально. Ответ: 2 л. Рефлексия. Итоги урока. Дом зад. Задача. Смешали 30% и 10% растворы соляной кислоты и получили 600 г 15% раствора. Сколько граммов каждого раствора было взято? Приложение 10. Тема. «Задачи на сплавы различными способами» (тема 7) Цель урока. Повторение способов решения задач на смеси и сплавы. Изучить метод «площади равновеликих прямоугольников». Ход урока: Орг. момент Беседа. (сообщение необходимости решения задач на смеси и сплавы, связь темы с практическим применением). В связи с этим появилась необходимость в усилении практической направленности обучения, включении в работу с учащимися соответствующих заданий на проценты, пропорции, графики реальных зависимостей, текстовые задачи с построением математических моделей реальных ситуаций. В процессе поиска решения этих задач полезно применить очень удобную модель: Изображаем каждую смесь (сплав) в виде прямоугольника разбитого на фрагменты, количество которых соответствует количеству составляющих эту смесь (этот сплав) элементов. Актуализация опорных знаний Человеку часто приходится смешивать различные жидкости, порошки, газообразные или твердые вещества, или разбавлять что-либо водой. Текстовые задачи на смеси, сплавы и растворы входят в различные сборники заданий по математике ГИА и ЕГЭ. «Закон сохранения объема или массы» Если два сплава (раствора) соединяют в один «новый» сплав (раствор), то V = V1 + V2 – сохраняется объем; m = m1+ m2 – сохраняется масса. Примеры: Если сплав содержит свинец и медь в отношении 4:7, то в этом сплаве 4/11 частей от массы сплава составляет масса свинца, а 7/11- масса меди. Немного теории. Абсолютное содержание вещества в смеси – это количество вещества, выраженное в единицах измерения (грамм, литр и др.) Относительное содержание вещества в смеси – это отношение абсолютного содержания и общей массы (объему) смеси. Часто относительное содержание вещества в смеси называют концентрацией или процентным содержанием. Сумма концентраций всех компонентов смеси равна 1. Если имеется 40%-й раствор соли, то в этом растворе 0,4 объема занимает «чистая» соль. Значит, объемная концентрация соли в растворе равна 0,4. Закрепление материала (решение задач на смеси, растворы и сплавы разными способами). Задача 1. Решите самостоятельно. Два литра шести процентного уксуса разбавили тремя литрами одно процентного уксуса. Каково процентное содержание уксуса в полученном растворе? (Ответ: 3). Задача 2. Имеются сплавы золота и серебра. В одном эти металлы находятся в отношении 2: 3, а в другом в отношении 3: 7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11? Решение.  По этой схеме уравнение х + у =1 показывает массу нового сплава. Определяем массу золота в каждом сплаве и получаем уравнение Аналогично массу серебра и получаем уравнение Записываем одну из систем: 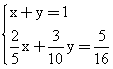 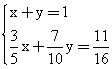 Решая ее, получаем х = 0,125 и у = 0,875 Ответ: 125 г и 875 г. Решение задач с помощью схем и графиков. В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы, рисунки, таблицы. Современные психологи утверждают, что решение одной задачи несколькими способами часто бывает более полезным, чем решение одним способом нескольких задач. Поэтому мы с вами рассмотрим несколько способов решения задач на смеси и сплавы. В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы, иллюстративные рисунки или вспомогательные таблицы. Рассмотрим их. Задача. Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди. Рассмотрим решение этой задачи двумя способами с помощью уравнения и систем уравнений.  х = 140 и у = 60 Ответ: 140 г меди и 60 г свинца Задача. Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. Сколько граммов каждого раствора надо было взять? Решение 1: Обозначим x массу первого раствора, тогда масса второго (600 - x). Составим уравнение: 30x + 10* (600 - x) = 600 *15 x = 150 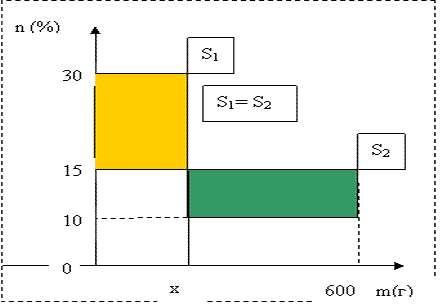 Решение 2: Приравнивание площадей равновеликих прямоугольников: 15x = 5 (600- x) x =150 Ответ: 150 г 30% и 450 г 10% раствора Задача. Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого из этих сортов, чтобы получить140 т стали с содержанием 30% никеля? 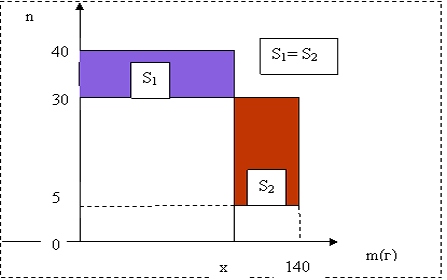 С использованием графика: (приравнивание площадей равновеликих прямоугольников) 10*х = 25*(140 – х) х = 100 140 – 100 = 40 Ответ: 100 т и 40 т Закрепление материала, путем решения задач. Решение у доски. Задача. Имеется два кислотных раствора: один 20%, другой 30%. Взяли 0,5 л первого и 1,5 л второго раствора и образовали новый раствор. Какова концентрация кислоты в новом растворе? Решение. Так как первый раствор 20 % - й, то в нем 0,2 объема занимает «чистая» кислота. Так как объем первого раствора равен 0,5л, то в этом количестве содержится 0,2*0,5=0,1 л «чистой» кислоты. Аналогично во втором растворе будет содержаться 0,3*1,5=0,45л «чистой» кислоты. При смешивании обоих растворов получим 0,5+1,5=2л кислотного раствора, в котором 0,1+0,45=0,55л «чистой» кислоты. Отсюда следует, что концентрация кислоты в новом растворе есть отношение 0,55:2=0,275, т.е.27,5%. Ответ: концентрация кислоты в новом растворе 27,5% Задача. Имеется руда из двух пластов с содержанием меди 6% и 11%. Сколько «бедной» руды надо взять, чтобы получить при смешивании с «богатой» 20 т руды с содержанием меди 8%? Аналитическая модель: Переведем проценты в дроби: 6%=0,06; 11%=0,11; 8%=0,08 Пусть надо взять х т «бедной» руды, которая будет содержать 0,06х т меди, а «богатой» руды надо взять (20-х) т, которая будет содержать 0,11(20 - х) т меди. Так как получившиеся 20 т руды будут содержать 20*0,08 т меди, то получим уравнение: 0,06х + 0,11(20 - х) = 20*0,08. Решив уравнение, получим х = 12. Ответ: 12т руды с 6% содержанием меди Итоги урока. Домашнее задание. (Задачи из открытого банка задач ЕГЭ) Приложение 11. Урок. Зачетная работа по теме «Решение задач на смеси, сплавы, концентрацию» (тема 8). Основная цель: проверить результаты учебной деятельности по изученному материалу. Воспитывать интерес к предмету через межпредметные связи с химией, обращая внимание на аккуратность, дисциплинированность и самостоятельность. Развивать устную и письменную речь, внимание и логическое мышление. В результате учащиеся должны знать какие требования предъявляются к зачетной работе, понимать различия в задачах различного типа, уметь грамотно оформить свою работу, Использовать приобретенные умения и навыки в практической деятельности и повседневной жизни для - самоопределения в дальнейшей учебной деятельности, - самоутверждения в классном коллективе. Ход урока. 1. Сообщение темы и цели урока. 2. Характеристика зачетной работы. По сравнению с контрольной работой в зачетной увеличено количество заданий. Соответственно у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В, С. Самые простые находятся в части А, более сложные в части В. Еще сложнее в части С. Каждая задача из А оценивается в 1 балл, из В – 2 балла, из С – 3 балла. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В – 8 баллов, и блока С - 9 баллов (всего 24 балла). Оценка «3» ставится за 6 - 9 баллов, оценка «4» – за 10 – 16 баллов, оценка «5» – за 17 - 24 баллов. Так как работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного занятия можно и не посвящать (решения задач могут быть вывешены на стенде). 3. Для самостоятельного решения полезно предложить учащимся следующие задания: Задачи, используемые для итогового теста. А.
В.
10. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра составляет 14 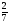 % веса меди. Сколько серебра в данном сплаве? % веса меди. Сколько серебра в данном сплаве?
С.
Разбор заданий зачетной работы. 1.Ответ:13,5кг. 2.Ответ:40т и 100т. 3.Ответ:2,5 кг 4.Ответ:40% и 25%. 5.Ответ:441г. 6.Ответ:150г. 7.Ответ: 60 кг. 8.Ответ:20%. 9.Ответ:5т 10.Ответ:0,25 кг. 11.Ответ:20% и 60% 12.Ответ:6 раз. 13.Ответ:400г. 14.Ответ:10кг; 69% Итоги урока. Учитель: закончить сегодняшний урок я бы хотела следующими словами: «Необходимо всегда глубоко продумывать сущность любой задачи и находить рациональные способы её решения, а не просто подгонять под ответ в конце учебника». Л. М. Фридман. Приложение 12. БАНК ЗАДАНИЙ ИЗ ВАРИАНТОВ ГИА, ЕГЭ. 2012г
Приложение 13. Задачи из открытого банка задач ГИА 2014 г.
Приложение 14. Задачи из открытого банка задач ЕГЭ 2014г.
Приложение 15. Банк задач на смеси, сплавы, концентрацию. Задачи на сплавы (тема 2).
50% меди? 7. Бронза – сплав меди и олова. В древности из бронзы отливали колокола, если в ней содержалось 75% меди. К куску бронзы 500кг и содержащему 72% добавили некоторое количество бронзы, содержащей 80% меди и получили бронзу, необходимую для изготовления колокола. Определите сколько добавили 80% бронзы. 8. Имелось два слитка меди. Процент содержания меди в первом слитке на 40% меньше, чем во втором. После того как оба слитка сплавили, получился слиток, содержащий 36% меди. Найдите процентное содержание меди в каждом слитке, если в первом было 6 кг меди, а во втором — 12 кг.
Приложение 16. Задачи на растворы на понижение концентрации ( |