англйиский для школьников киров У вас должен быть включен JavaScript для просмотра. . Сайт не несет ответственности за использование (как правомерное, так и неправомерное) третьими лицами информации, размещенной Пользователем на Сайте, включая её воспроизведение и распространение, осуществленные всеми возможными способами. Сайт имеет право вносить изменения в настоящее Соглашение.
Исследовательская работа «Лента Мёбиуса»
 Скачать 130.56 Kb. Скачать 130.56 Kb.
|
| Муниципальное бюджетное общеобразовательное учреждение «Березовская средняя общеобразовательная школа» Первомайского района Алтайского края Исследовательская работа «Лента Мёбиуса» Выполнила: ученица 7 б класса МБОУ «Березовская СОШ» Колупаева Вера Руководитель: Семенченко Светлана Петровна, учитель математики с. Березовка, 2012 г. СОДЕРЖАНИЕ Введение Биография Мёбиуса Августа Фердинанда Свойства ленты Мёбиуса Эксперименты над листом Мёбиуса Применение ленты Мебиуса Выводы Литература Приложение Введение Во многих парках и скверах, и даже в художественных музеях можно встретить удивительные скульптуры. У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. В 1967 году в Бразилии состоялся международный математический конгресс. Его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена лента Мёбиуса. И монумент высотой более чем в два метра, и крохотная марка – своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу, профессору Лейпцигского университета. Что это за лента и почему она вызывает такой интерес у художников и скульпторов? Оказывается это – лента Мебиуса, и она имеет самое прямое отношение к математике. Мне захотелось, как можно больше узнать об этой загадочной ленте Мебиуса. Целью моей исследовательской работы было: - изучение свойств ленты (листа) Мебиуса; - изучение применения ленты Мёбиуса. Для достижения поставленной цели мною решались следующие задачи: - познакомиться с историей появления ленты Мебиуса; - изготовить ленту Мебиуса; - исследовать опытным путем свойства ленты Мебиуса; - установить области применения ленты Мебиуса. Объект исследования: лента Мебиуса. Предмет исследования: свойства ленты Мёбиуса. Гипотеза: односторонние поверхности существуют. В своей работе я использовала методы: - анализ литературы по теме; - сравнение; - обобщение; - моделирование ; - эксперимент. Биография Мёбиуса Августа Фердинанда Август Фердинанд Мёбиус (1790-1868)(см. Приложение 1) родился на территории княжеской школы Шульпфорте, близ Наумбурга (Саксония-Анхальт). Его отец занимал в этой школе должность учителя танцев. Мать Мёбиуса была потомком Мартина Лютера. Отец умер, когда мальчику было всего три года. Начальное образование Мёбиус получил дома и сразу показал свой интерес к математике. С 1803 по 1809 годы учился в колледже Шульпфорте, затем поступил в Лейпцигский университет. Первые полгода, в соответствии с рекомендациями семьи, он изучал право, но затем принял окончательное решение посвятить жизнь математике и астрономии. Биографы предполагают, что в этом выборе сказалось влияние преподававшего там известного астронома и математика Моллвейде. В 1813—1814 годах Мёбиус жил в Гёттингене, где посещал университетские лекции Гаусса по астрономии. Затем он уехал в Халле, чтобы прослушать курс лекций математика Иоганна Пфаффа, учителя Гаусса. В результате Мёбиус получил глубокие знания по обеим наукам. С 1816 года он также работал сначала астрономом-наблюдателем, затем директором в Плейсенбургской астрономической обсерватории (близ Лейпцига). Деятельно участвовал в перестройке и оснащении обсерватории. В 1820 году Мёбиус женился. У него родились два сына и дочь. В 1825 году Моллвейд умер. Мёбиус попытался занять его место, но его репутация преподавателя была неважной, и университет предпочёл другую кандидатуру. Однако, узнав, что Мёбиус получил приглашения из других университетов, руководство повысило его в должности до ординарного профессора астрономии. К этому времени математические исследования Мёбиуса принесли ему известность в научном мире. В 1848 году Мёбиус становится директором обсерватории. В возрасте 68 лет Августу Мёбиусу удалось сделать открытие поразительной красоты. Он открыл односторонние поверхности, одна из которых – лист Мёбиуса. Лента Мёбиуса относится к числу «математических неожиданностей». А случилось это открытие в 1858 г. Рассказывают, что открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты. Мёбиус послал в Парижскую академию наук работу, включавшую сведения об этом листе. Семь лет он дожидался рассмотрения своей работы и, не дождавшись, опубликовал ее результаты. Справедливости ради, надо отметить, что почти в это же время предложил в качестве первого примера односторонней поверхности этот лист и другой ученик К.Ф. Гаусса – Иоганн Бенедикт Листинг, профессор Геттингенского Университета. Свою работу он опубликовал на три года раньше, чем Мёбиус, - в 1862 году, но лента все-таки носит имя Мёбиуса. Свойства ленты Мёбиуса Лист Мебиуса получается очень просто: надо склеить из бумажной полоски кольцо, только перед склеиванием повернуть один конец на 180° (см. Приложение 2). Что же удивительного в этой ленте? – Это ее свойства. 1. Односторонность. У листа Мёбиуса – всего одна сторона 2. Непрерывность. На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом ни разу не придётся переползать через край “ленты”. Разрывов нет – непрерывность полная. 3. Связность. Лист Мёбиуса двусвязен, т.к. если разрезать его вдоль, он превратится не в два отдельных кольца, а в одну целую ленту. 4. Неориентированность. Так, если бы человек смог пропутешествовать по всем изгибам листа Мёбиуса, то когда он вернулся бы в исходную точку, он превратился в своё зеркальное отражение. Эксперименты над листом Мёбиуса Чтобы понять некоторые свойства ленты Мебиуса я провела несколько экспериментов, взяв в качестве объектов – обычную ленту и ленту Мебиуса (см. Приложение 3). Опыт 1. Поставим точку на одной стороне каждого кольца и начертим непрерывную линию вдоль него, пока не придем снова в отмеченную точку. У обычного кольца линия проходит вдоль по одной стороне, сходясь в точке начала, вторая сторона остается чистой. У ленты Мёбиуса линия проходит по двум сторонам, заканчиваясь в начале. Опыт 2. Закрасим полностью только одну сторону колец. У обычного кольца – одна сторона закрашена, другая –нет. У ленты Мёбиуса –лента закрашена целиком. Таким образом, можно сделать вывод, что лента Мёбиуса имеет одну поверхность. Опыт 3. Закрасим непрерывной линией только один край колец. Закрасим узенькую полоску края ленты. У обычной ленты – один край кольца закрашен, второй – нет. У ленты Мёбиуса – линия края непрерывно закрашена на всем кольце. Значит лента Мёбиуса имеет один край. Опыт 4. На внутреннюю сторону обычного кольца посадим зайца, а на наружную волка. Разрешим им бегать как угодно, запретив перелезать через края кольца. На обычном кольце заяц и волк никогда не встретятся, не пересекая края. На ленте Мёбиуса они встретятся, не пересекая края. Значит Лента Мебиуса имеет одну искривленную поверхность, и если по ней двигаться, можно с внутренней части переместиться на внешнюю. Опыт 5. Разрежем кольца пополам вдоль. У обычного кольца получилось два кольца, уже, чем исходное, причем длина окружности каждого будет такой же, как длина окружности первоначально взятого. У ленты Мёбиуса получилось одно большое кольцо в виде восьмёрки. Опыт 6. Разрежем кольцо вдоль, отступив от края 1/3. У обычного кольца получилось 2 кольца одно уже, другое шире. У ленты Мёбиуса получилось два сцепленных друг с другом кольца, одно маленькое – другое большое. Опыт 7. Опыты с многоразовым разрезанием показали, что у обычного кольца получаются кольца все уже и уже, но длина окружности остается одинаковой. У ленты Мёбиуса: - при разрезании на чётное число полосок получаются только большие сцепленные кольца, которых в два раза меньше, чем количество разрезов (полосок); - при разрезании на нечётное число полосок получаются одно маленькое и несколько больших колец, сцепленных с маленьким, которых тоже в 2 раза меньше разности между количеством разрезов и маленьких колец. Применение ленты Мебиуса 1. Лист Мёбиуса в науке и технике (см. Приложение 4). Существовали технические применения ленты Мёбиуса. Патентная служба зарегистрировала немало изобретений, в основе, которых лежит всё та же односторонняя поверхность. В 1923 году выдан патент изобретателю Ли де форсу, который предложил записывать звук на киноленте без смены катушек, сразу с двух сторон. Придуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания. В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса. В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде листа Мёбиуса. Полоса ленточного конвейера выполнялась в виде ленты Мёбиуса, что позволяло ему работать дольше, потому что вся поверхность ленты равномерно изнашивалась. В матричных принтерах красящая лента имела вид листа Мёбиуса для увеличения срока годности. 2. Лист Мёбиуса в живописи и архитектуре. - Муравьи на листе Мёбиуса. Рисунок Мориса Эшера(см. Приложение 5) - Памятник трём бесконечностям в Латвии. - У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. В 1967 году, когда в Бразилии состоялся международный математический конгресс, его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена лента Мёбиуса. И монумент высотой более чем в два метра, и крохотная марка – своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу, профессору Лейпцигского университета. Мотив Ленты Мебиуса встречается в названиях художественных произведений, общественных заведений, логотипах (см. Приложение 6). 3. Лента Мебиуса в цирковом искусстве. Лента Мебиуса понравилась не только математикам, но и фокусникам. Более 100 лет лист Мёбиуса используется для показа различных фокусов и развлечений. Удивительные свойства листа демонстрировались даже в цирке, где подвешивались яркие ленты, склеенные в виде листов Мёбиуса. Фокусник закуривал сигарету и горящим концом дотрагивался до средней линии каждой ленты, которая была выполнена из калийной селитры. Огненная дорожка превращала первую ленту в более длинную, а вторую - в две ленты, продетая одна в другую. (В этом случае фокусник разрезал лист Мёбиуса не посередине, а на расстоянии в одну треть его ширины). Фокусники используют лист Мебиуса уже на протяжении 75 лет. Вот пример еще одного фокуса: фокусник вручает зрителю три больших бумажных кольца, каждое из которых получилось путем склеивания концов длинной ленты. Зритель разрезает ножницами первое кольцо вдоль ленты посередине, пока не вернется в исходную точку. В результате получаются два отдельных кольца. Разрезая таким же образом второе кольцо, он получает, к своему удивлению, не два кольца, а одно, которое вдвое длиннее исходного. Наконец, разрезая третье, он снова получает поразительный результат: два кольца, сцепленных друг с другом. Результат этого фокуса зависит от того, как были сомкнуты концы ленты перед склейкой. Первое наше кольцо получилось путем простого соединения концов ленты без перекручивание. Второе кольцо получается при соединении концов ленты, перекрученной один раз на 180ْ. Третье кольцо получилось при разрезании ленты, концы которой перекручивались перед склейкой дважды. Известно еще много фокусов с применением ленты Мебиуса. 4. Лента Мебиуса и генетика. Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение. Или аннигиляция, как подтверждают физики. Они, кстати, утверждают также, что все оптические законы основаны на свойствах ленты Мебиуса, в частности отражение в зеркале – это своеобразный перенос во времени, краткосрочный, длящийся сотые доли секунды, ведь мы видим перед собой… правильно, зеркального своего двойника! Выводы Несмотря на то, что Мёбиус сделал своё удивительное открытие очень давно, оно очень популярно и в наши дни: - у математиков- идут дальнейшие исследования; - у школьников - очень интересно экспериментировать с лентой Мёбиуса; - у учителей – есть ещё один способ заинтересовать учеников математикой; - в технике – открываются всё новые способы использования ленты Мёбиуса. Мёбиус повлиял не только на математиков, но и на художников, скульпторов, архитекторов и многих, многих других. В результате появились картины, скульптуры, марки, и прочие произведения искусства с изображением ленты Мёбиуса. Я думаю, что следов Мёбиуса в искусстве будет ещё много. Лист Мёбиуса – удивительный феномен. Его можно исследовать до бесконечности и рассказывать о Ленте Мебиуса можно удивительно долго. Надеюсь, что я вас заинтересовала, и вы продолжите исследования этого непредсказуемого листа сами, набрав в интернете заветное слово. Литература
ПРИЛОЖЕНИЯ Приложение 1. Август Фердинанд Мёбиус (1790-1868)(  Приложение 2. Как склеить ленту Мёбиуса. 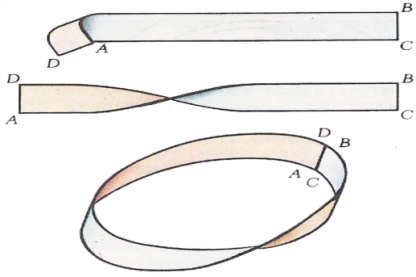 Приложение 3. Эксперименты с лентой Мёбиуса и обычным кольцом
Приложение 4. Лист Мёбиуса в технике  Приложение 5. Лист Мёбиуса в живописи и архитектуре. Муравьи на листе Мёбиуса. Рисунок Мориса Эшера.    Памятник трём бесконечностям в Латвии Кулон «Лента Мёбиуса»   Скульптор Макс Билл и Мёбиус Музей воды в Санкт-Петербурге     Творчество неизвестных мастеров Приложение 6. Мотив Ленты Мебиуса в названиях художественных произведений, общественных заведений, логотипах | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






