Контрольно-оценочные материалы для комплексного экзамена по результатам освоения дисциплины Математика, входящей в общеобразовательный цикл и относящейся к базовым общеобразовательным
 Скачать 93.34 Kb. Скачать 93.34 Kb. |
    Контрольно-оценочные материалы для комплексного экзамена Контрольно-оценочные материалы для комплексного экзаменапо результатам освоения дисциплины Математика, входящей в общеобразовательный цикл и относящейся к базовым общеобразовательным дисциплинам СПО (Уровень подготовки – базовый) 1.1. Назначение контрольно-оценочных материалов Контрольно-оценочные материалы предназначены для промежуточной аттестации в форме письменного экзамена по результатам освоения дисциплины «Математика». 1.2. Перечень знаний и умений, подлежащих контролю. Знания: • значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе; • значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии; • универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; • вероятностный характер различных процессов окружающего мира. • свойства степеней, корней, логарифмов; формулы, связанные со свойствами степеней, логарифмов. • тригонометрические формулы для преобразования выражений. • методы решения уравнений и неравенств. • формулы производных функций, формулы интегрирования. • формулы сложения, умножения вероятностей, формулу полной вероятности. • аксиомы стереометрии и теоремы о взаимном расположении прямых и плоскостей в пространстве • формулы для нахождения площадей и объемов геометрических тел; В том числе: Использовать приобретенные знания и умения в практической деятельности и повседневной жизни: • для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства. • для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков. • решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения. • для построения и исследования простейших математических моделей. • для анализа реальных числовых данных, представленных в виде диаграмм, графиков; • анализа информации статистического характера. • для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур; • вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства. Умения: • выполнять арифметические действия над числами, сочетая устные и письменные приемы; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения; • находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах; • выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций; • вычислять значение функции по заданному значению аргумента при различных способах задания функции; • определять основные свойства числовых функций, иллюстрировать их на графиках; • строить графики изученных функций, иллюстрировать по графику свойства элементарных функций; • использовать понятие функции для описания и анализа зависимостей величин; • находить производные элементарных функций; • использовать производную для изучения свойств функций и построения графиков; • применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения; • вычислять в простейших случаях площади и объемы с использованием определенного интеграла; • решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы; • использовать графический метод решения уравнений и неравенств; • изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными; • составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задачах. • решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул; • вычислять в простейших случаях вероятности событий на основе подсчета числа исходов; • распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями; • описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении; • анализировать в простейших случаях взаимное расположение объектов в пространстве; • изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; • строить простейшие сечения куба, призмы, пирамиды; • решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); • использовать при решении стереометрических задач планиметрические факты и методы; • проводить доказательные рассуждения в ходе решения задач; 2. Экзаменационные задания и материально – техническое оснащение экзамена: 2.1 Время, отведённое на проведение письменного экзамена по математике – 2 часа 2.2 Содержание экзаменационной работы: Экзаменационные задания в виде экзаменационных работ, состоящих из двух частей и содержит 29 заданий. Часть I содержит 21 тестовое задание базового уровня по материалу курса математики. В каждом задании кратко излагается условие задачи или примера. К каждому заданию предлагается 4 варианта ответов, 1 из которых - правильный. Задания части I считаются выполненными, если экзаменуемый выбрал верный ответ. За каждый верный ответ в задании части I экзаменационной работы студент получает 2 балла; при неверном выборе ответа, но верном ходе решения - 1 балл, при неверном выборе ответа и неверном решении или отсутствии решения – 0 баллов. Часть II содержит 8 более сложных заданий по материалу курса математики. Задания части II экзаменационной работы выполняются на отдельных листах, где записываются подробные решения с разъяснениями, чертежами, графиками и т.д. За каждое задание части II студент получает до 3 баллов, в зависимости от объёма правильно выполненных операций и рассуждений в процессе решения каждого из предложенных заданий. (Все необходимые вычисления, преобразования и чертежи учащиеся могут производить в черновике.) Баллы, полученные за выполненные задания, суммируются 2.3. материально – техническое оснащение экзамена: - экзаменационные листы с заданиями - чистые листы для выполнения решения - чистые листы для черновика - студентам разрешается использовать справочные материалы, содержащие основные формулы курса математики. - линейка. 3.3. Критерии оценки:
Критерии оценки письменной экзаменационной работы по математике согласно набранных баллов: 5 «отлично» – 60 баллов – 66 баллов 4 «хорошо» – 52 балла – 59 баллов 3 «удовлетворительно» – 44 балла – 51 балл 2 «неудовлетворительно» – менее 44 баллов Примеры заданий письменной экзаменационной работы по математике:
А) 3 х+1 = 27х -1 Б) lοg 2 (х+2) = 3 В) 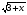 = 3 Г) = 3 Г) 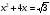
А) 8 Б) - 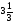 В) В) 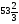 Г) 10,2 Г) 10,23. Вычислите и укажите значение выражения: lοg 2 32 - lοg 3 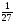 - lg 1 - lg 1А) 10 Б) 9 В) 8 Г) 7 Вычислите и укажите значение выражения: 2sin30º + cos π – tg 2π А)  Б) Б) 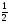 В) 1,5 Г) 0 В) 1,5 Г) 05. Решите уравнение и укажите его корни: 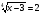 А) 20 Б) 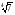 В) 19 Г) 8,5 В) 19 Г) 8,56. Решите уравнение и укажите его корни: 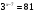 А) -7 Б) 10 В) 11 Г) 0 7. Укажите решения неравенства: 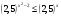 А) х ≥ 2 Б) -1 < х ≤ 2 В) х ≤ 2 Г) х 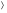 -1 -18. Решите уравнение и укажите его корни: А) -7 Б) 10 В) 11 Г) 0 7. Укажите решения неравенства: 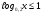 А) х ≥ 0,2 Б) 0 < х ≤ 0,2 В) х ≤ 0,2 Г) х 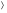 0 08. Укажите, на каком рисунке изображен график функции 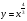 А) у Б) у В) у Г) у 1 1 1 1 1 0 х 0 -1 0 1 х -1 0 1 х -1 -1 1 9. Укажите функцию, являющуюся чётной: А) у = sinх Б) у = сosх В) у = tgх Г) у = ctgх 10. Укажите функцию, являющуюся периодической: А) у= lg(х+5) Б) у =  В) у = cos 2х Г) В) у = cos 2х Г) 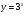 11. Вычислите предел ℓim (4х – 7х2) : х→2 А) -1 Б) 2 В) -20 Г) 3 12. Вычислить производную 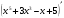 А) 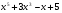 Б) Б)  В) В) 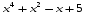 Г) Г) 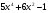 13. Вычислить интеграл: 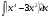 А) 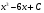 Б) Б) 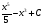 В) В)  Г) Г) 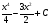 14. Вычислить интеграл: 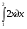 А) 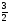 Б) 2 В) -1 Г) 3 Б) 2 В) -1 Г) 315. Какое из перечисленных геометрических тел не является телом вращения: А) цилиндр Б) сфера В) конус Г) тетраэдр 16. Объём какой геометрической фигуры вычисляется по формуле V= 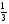 π r² h π r² hА) цилиндр Б) пирамида В) конус Г) призма 17. Найдите координаты вектора  : :А) 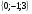 Б) Б) 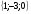 В) В) 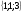 Г) Г) 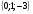 18. Найдите длину вектора  : :А)  Б) 1 В) Б) 1 В)  Г) 3 Г) 319. Найдите скалярное произведение векторов 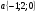 и и 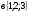 : :А) 2 Б) -5 В) 7 Г) 3 20. Какое из выражений является уравнением сферы с центром О(-2;0;1) и радиусом равным  : :А) (х+2)² + у² + (z-1)² = 25 Б) (х-2)² + у² + (z+1)² = 25 В) (х+2)² + у² + (z-1)² = 5 Г) (х-2)² + у² + (z+1)² = 5 21. Какая из перечисленных геометрических фигур является осевым сечением прямого цилиндра: А) равнобедренная трапеция Б) прямоугольник В) круг Г) равнобедренный треугольник II часть №1. Решить уравнение: 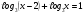 №2. Решить неравенство: 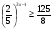 №3. Упростить выражение: 3cos2α + sin²α - cos²α №4. Написать уравнение касательной к графику функции  в точке в точке 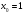 №5. Найти площадь фигуры, ограниченной линиями 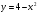 и осью Ох и осью Ох№6. Вычислить площадь полной поверхности и объём правильной четырёхугольной призмы, каждое ребро которой равно 4дм. №7. Найти площадь поверхности и объём фигуры, полученной вращением равностороннего треугольника со стороной 2м вокруг одной из его сторон. №8. Найти длину медианы АМ треугольника АВС, если А(2;-3;1), В(0;4;-2), С(-4;2;0). Основные вопросы для подготовки к экзамену по математике:
| |||||||||||||||||