Мбоу сош №4 с уиоп им. Г. К. Жукова
 Скачать 192.33 Kb. Скачать 192.33 Kb.
|
Содержание.
Введение. Развивающее обучение – это обучение, которое непосредственно ориентировано на закономерности развития личности. Это обучение, в котором развивающий эффект является не побочным, а прямым результатом. Оно рассматривает ученика как личность, живущую сегодня, и создает максимум благоприятных условий для ее развития, «… развивающее обучение есть развитие субъекта». Поэтому я стараюсь строить свои уроки не на авторитарных отношениях, а на субъектно-субъектных, помня, что я не вправе никому отдавать предпочтение. В ходе применения развивающего обучения происходит стимулирование познавательной деятельности, активизация процессов самопознания, саморазвития, самообразования. Основной мотивацией учебной деятельности в системе развивающего обучения является познавательный интерес с учетом профессиональной направленности. Для этого я вовлекаю учащихся в различные виды деятельности: математический КВН, доклады, различные игры, конкурсы, привлекаю учащихся к оформлению кабинета. Но все же основным элементом образовательного процесса был и остается урок. Я стараюсь, чтобы на уроках дети вели самостоятельный поиск решений задач и примеров. Объяснение нового материала часто начинается с задачи (создание проблемной ситуации), в ходе решения которой учащиеся сами приходят к необходимому выводу. Цели исследования.
Принципы развивающего обучения Страшная это опасность – безделье за партой; безделье шесть часов ежедневно, безделье месяцы и годы. Это развращает, морально калечит человека, и ни школьная бригада, ни школьный участок, ни мастерская – ничто не может возместить того, что упущено в самой главной сфере, где человек должен быть тружеником, - в сфере мысли. В. А. Сухомлинский [12]. Перечислю принципы развивающего обучения, используемые в своей деятельности:
Эффективность педагогического процесса обусловлена наличием постоянной обратной связи, которая позволяет получать информацию о соответствии полученных результатов предъявляемым требованиям, что составляет контрольно-оценочный, или рефлексивный, компонент педагогической деятельности. Результатом использования системы развивающего обучения является развитие мышления учащихся, и, как следствие, низкий процент неуспевающих по математике, победы учащихся на зональных олимпиадах, поступление выпускников в вузы, где математика является профилирующим предметом. В традиционном обучении система понятий задается для усвоения через формулировку этих понятий, их определения. Поэтому существует жесткий перечень, что должен знать ученик. В развивающем обучении научные понятия существуют в легком варианте – способе действий. Ребёнком должен быть освоен этот способ, его основание, умение построить данное действие, обосновать, доказать его. Поэтому в развивающем обучении нежелательно и, по-видимому, невозможно задавать готовые определения. Формулировка понятия – это тот результат, к которому нужно прийти в конечном итоге, в результате анализа. Изменение в содержании приводит и к существенному изменению методах обучения. Внутрипредметными и межпредметными связями в дидактических исследованиях по теории и методике обучения математике раскрываются закономерности процесса обучения: оптимизации и построения оптимальных дидактических систем; проблемного обучения математической деятельности; реализации деятельностного подхода посредством задач; формирования у учащихся способов деятельности, находящих применение в рамках нескольких предметов. При этом опора на межпредметные связи открывает возможность учить не отдельным действиям, а системе действий, т.е. системе приемов учебной деятельности. Приёмы учебной деятельности в обучении математике.
Приёмы деятельности могут быть разной степени сложности и обобщённости. Сложный приём состоит из большего числа действий, включает в себя в качестве составляющих действий другие приёмы, он необходим для решения более сложных задач. Обобщённый приём получен на основе анализа менее общих приёмов путём выделения общего содержания деятельности по решению конкретных учебных задач. Сознательное владение каким-либо приёмом деятельности называется умением; умение, доведённое до реально возможного автоматизма, характеризуется как навык. Если при наличии умения человек вынужден осуществлять оперативный контроль за выполнением действий, то на уровне навыка он специально не обдумывает каждый элемент деятельности (хотя при необходимости может это свободно сделать). Итак, термины «умение» и «навык» отражают разный уровень сформированности соответствующих действий и операций. На основе того, структуру каких компонентов они отражают, выделяют программы трех уровней: 1) исполнительские, 2) информационные и исполнительские, 3) мотивационно-целевые, информационные и исполнительские. Якиманская И. С. различает такие понятия, как «приём» и «способ» [14]. Приём в виде образца, алгоритма, правила должен входить в содержание знаний и описываться в учебнике или задаваться учителем. Способ – это открытие самого ученика, в нём проявляется накопленный учеником опыт познания; это – устойчивое индивидуальное образование, включающее в себя мотивационную и операционную сторону познавательной деятельности, - характеризует индивидуальную избирательность ученика к проработке учебного материала разного научного содержания, вида и формы, устойчивость предпочтения, продуктивность использования знаний. Усваиваемые в процессе учения общие приёмы учебной деятельности должны трансформироваться в его индивидуальные способы, в результате чего происходит обогащение личного опыта, усвоение знаний и развитие ученика.
1) учебно-организационные (определение задач, рациональное планирование, создание благоприятных условий деятельности), 2) учебно-информационные (работа с книгой и другими источниками информации, библиографический поиск, наблюдение), 3) учебно-интеллектуальные (мотивация деятельности, восприятие, осмысление, запоминание информации, решение проблемных задач, самоконтроль учебно-познавательной деятельности). Классификация приёмов учебной деятельности учащихся при изучении математики учитывает особенности её содержания и основных задач и может быть проведена по различным основаниям как в отношении обще-учебных приёмов (умственной деятельности, решения задач), так и в отношении отдельных курсов, разделов и тем школьного курса математики. «Квадратичная функция. График, свойства и их применение». Начинаю с подготовительной работы по следующему плану:
Итак, на доске или на плакатах я заранее подготавливаю восемь видов графиков (рис. 1):  Рис. 1 Графики квадратичной функции. По этим рисункам с классом обсуждаю особенности каждого графика и их общие свойства. Особое внимание уделяю тому, что изображённые кривые являются графиками различных квадратичных функций, и ввожу термин для обозначения кривых такого вида – «парабола», а также новые термины «вершина», «ветви», заостряя внимание на том, что каждая парабола имеет одну вершину и две ветви. При дальнейшем обсуждении графиков, ученики устанавливают факт, что у каждой параболы ветви направлены или только вверх или только вниз, вершина может располагаться или в начале координат (рис.1,а,б), или во внутренней части квадранта (рис.1,в,д,з), или на осях (рис.1,г,е,ж). Далее, я обращаю внимание ребят на точки пересечения с осями координат Ох и Оу. Сколько точек пересечения может иметь парабола? Решая эту проблему, я акцентирую внимание на следующем: симметричность расположения ветвей параболы относительно оси симметрии, направление ветвей, расположение параболы относительно осей. Так формируются первичные знания учащихся. Для закрепления этих знаний я ребятам даю следующие задания.
Ученики строят графики в своих тетрадях, а я вызываю нескольких человек к доске для того, чтобы каждый из них продемонстрировал свой чертёж на доске. Эту работу с учениками я провожу во избежание в дальнейшем ошибок при построении графика конкретной квадратичной функции. Теперь надо сформировать умения строить график квадратичной функции и перейти к методу построения, что обязательно должно быть усвоено всеми учащимися. Для этой цели в тетрадях записываем алгоритм построения:
Внимание! Данный алгоритм можно использовать для построения графика квадратичной функции любого вида, т.е. не только в том случае, когда функция записана в стандартном виде у = ах2 + bх + с, но и в других видах: y = ax2 + c; y = ax2 + bx; y = a(x +m)2 + n; y = a(x + m)2. Однако перед построением графика каждая функция должна быть приведена к стандартному виду, но в дальнейшем запись y = a(x +m)2 + n оказывается наиболее удобной, т.к. позволяет быстро определить координаты вершины. Но на первых порах я добиваюсь того, чтобы ученики приводили к стандартному виду, это целесообразней, так как связывает с понятием квадратного трёхчлена. Остаётся сформировать навык наиболее удобного и быстрого построения параболы. К уже изученному алгоритму добавляются формулы для вычисления вершины параболы: х0 = Вот здесь возникают большие трудности у учащихся, т.к. больше всего допускают ошибки при вычислении координат вершины параболы. Упростить вычисление можно следующим образом: зная, что х0 = В классах со слабой математической подготовкой такой метод построения параболы я считаю единственным и достаточным, а ещё более важно закрепить на конкретных примерах. Для группы таких ребят я даю примеры на закрепление этого алгоритма, а с сильными учениками разбираю второй метод. В первую очередь отрабатываю навыки построения симметричных точек, лежащих на ветвях параболы у = х2. Составляем таблицу зависимости значений функции от аргумента, по которой строится график. Цветными карандашами на одной и той же координатной плоскости ученики строят по точкам следующие графики: у = х2 +2; у = х2 – 4х +3; у = х2 + 5х. Обращаю внимание ребят на то, что при совмещении графиков, они одинаковы, а разница их лишь в расположении вершины параболы в координатной плоскости. Поэтому данные графики можно строить с помощью шаблонов, предварительно вычислив по коэффициентам a,b,c координаты вершины. С этой целью я предлагаю ребятам изготовить семь различных шаблонов: 1) у = х2; 2) у = 0,5х2; 3) у = 2х2; 4) у = Следующим этапом закрепления навыков построения квадратичной функции с использованием шаблонов параболы с ветвями направленными не вверх, а вниз: у = -х2; у = -х2 + 2; у = -х2 + 4х +3; у = -х2 +5х. Теперь необходимо обратить внимание на форму параболы с помощью построения графиков функций по точкам: у = 5х2, у = С учениками я анализирую вид построенных кривых, и по рисунку ребята устанавливают, как коэффициент «а» влияет на саму форму параболы. Если а>0 и а>1, то парабола тем сильнее прижимается к оси Оу, чем больше а. Если а>0 и a<1, то парабола более пологая и прижимается к оси Ох. 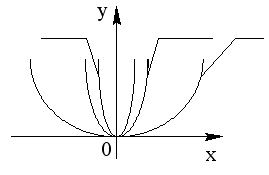 Также я обращаю внимание учеников на расположение графиков относительно графика у = х2, если коэффициент а положителен, то все квадратичные функции, у которых а>1, имеют графики, лежащие выше графика у = х2, если а положительно, но а<1, то графики квадратичных функций лежат ниже графика у = х2 , но точка х = 0 является исключением, т.к. это единственная точка, в которой графики совпадают. В конце урока, в целях проверки полученных знаний, умений и навыков, провожу самостоятельную работу:
у = На четвертом и пятом уроках обобщаю и систематизирую знания, умения и навыки. С этой целью мною подготовлен пакет задач с учетом межпредметных связей [11]:
А) Через сколько секунд упадёт на землю камень, брошенный с 80 – метровой башни со скоростью 7 м/с? Б) С самолета, летящего на высоте 700 м, на льдину сброшен груз с начальной скоростью 30м/с. Через сколько секунд груз достигнет льдины?
А) Футболист на тренировке подбрасывает ногой мяч вверх. Через сколько секунд мяч окажется в 10 м над землёй, если начальная скорость 15 м/с? Б) Футболист, подбрасывая мяч ногой, придал ему начальную скорость 20 м/с. Взлетит ли мяч выше берёзы, высота которой 15 м? Взлетит ли он выше дома, высота которого 22 м? 9*. С балкона, расположенного на высоте 20 м, бросили мяч под углом 30º вверх от горизонта со скоростью 10 м/с. Направив ось Х вдоль поверхности земли вправо, а ось У вдоль стены дома вверх, написать уравнения зависимости координат от времени х = х(t) и у = у(t), и уравнение траектории у = у(х). Найти: а) координаты мяча через 2 с; б) через какой промежуток времени мяч упадёт на землю; в) горизонтальную дальность полёта. Контроль и самоконтроль Важнейшими компонентами учебной деятельности является контроль и самоконтроль. Осуществляя контроль усвоения понятий сформированности умений, преследую следующие цели:
Приведу пример урока «Квадратные неравенства» Цели:
Оборудование: таблицы, шаблоны, карты – задания. Тип урока: урок обобщения и систематизации знаний. Ход урока:
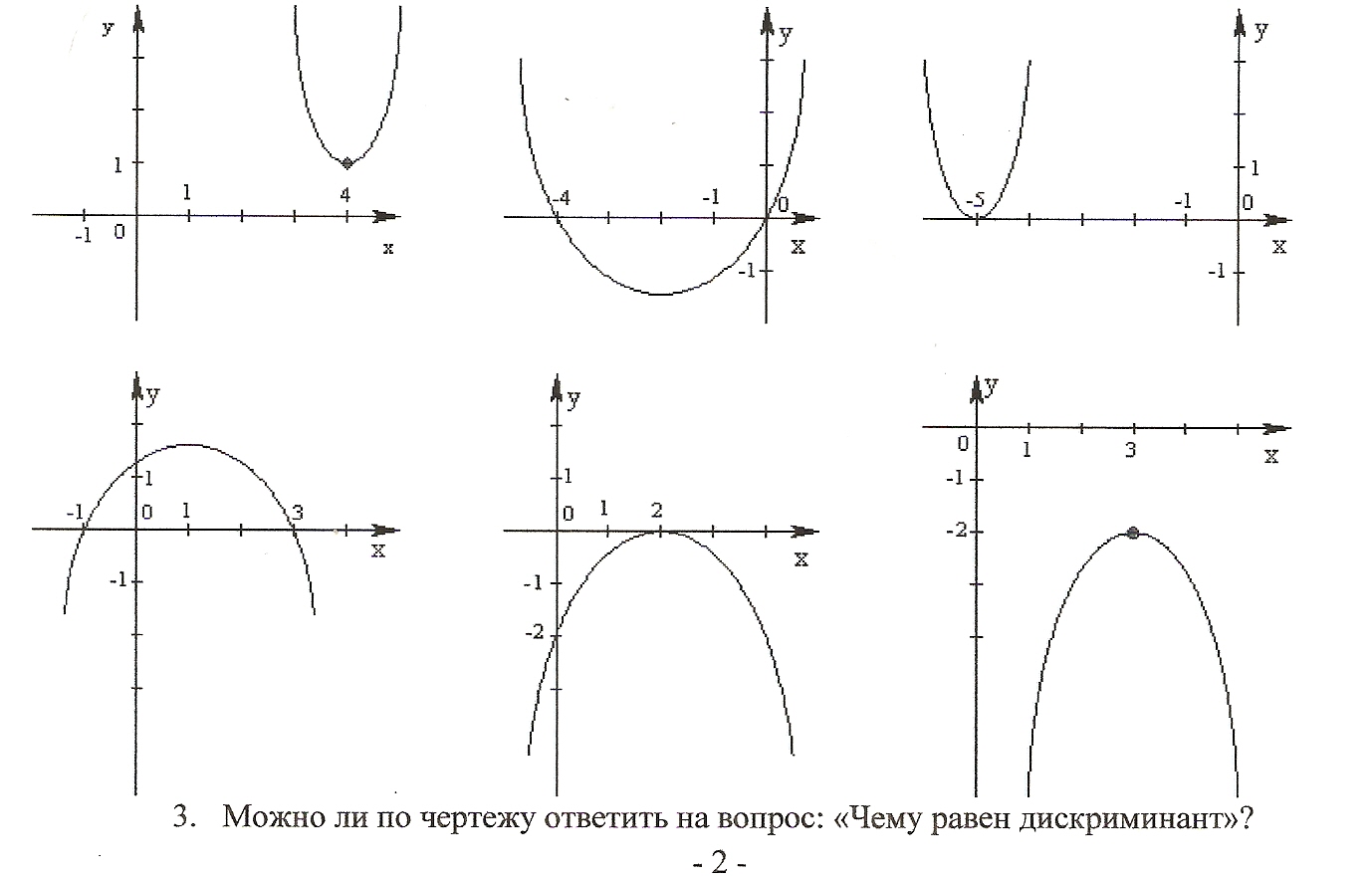 Рис. 2. Плакаты.
Вопрос учителя: «Как выяснить, является ли данное число решением или нет?» (Ответ: подставить это число в неравенство вместо х.) Решением является верное или неверное числовое неравенство:
7 > 0 – верно, да, является. 2. 1 – 2 – 3 < 0 -4 < 0 – верно, да, является. 3. -1 + 7 + 4 > 0 10 > 0 – верно, да, является.
19 < 0 – неверно, не является.
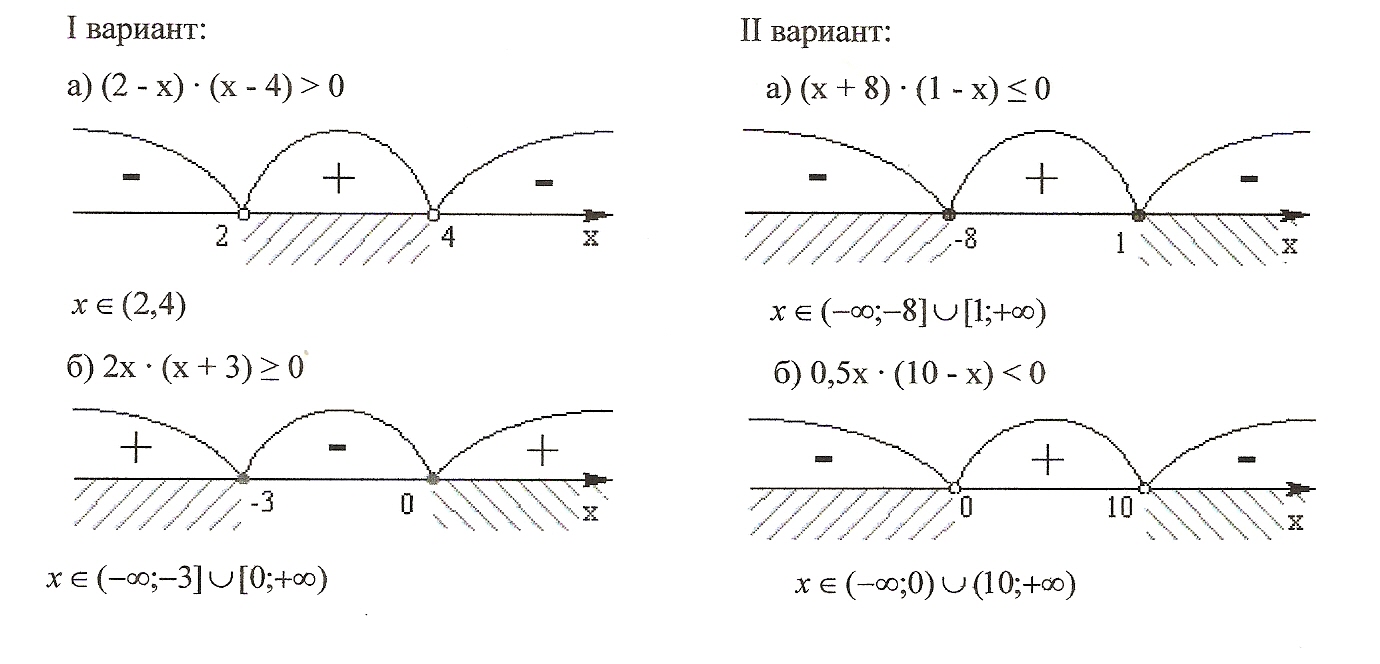
-3х2 + 4х -1 ≤ 0?  Решение (методом интервалов или графически): Нули функции: -3 + 4 – 1 = 0, следовательно. Х1 = 1, х2 = 1/3 (Ответ В.)
а) Какова область определения функции? F (x)= A: (0;3/5); Б:[0;3/5]; В: (-∞;0]U[3/5;+∞) Ученики решают самостоятельно и, найдя правильный ответ (В.), оформляют решение на доске, отвечая на вопрос: «Что называют областью определения функции?» б) Для какой из функций промежуток (-3;3) является областью ее определения? A. f(x)= Б. G(x)= В. H(x)= D(y) = (-3;3) - ? Решение (способ выбирают ученики по желанию). 9 – x2 ≥ 0 9 – x2 > 0 x2 – 9 > 0 (3 – х)(3 + х) ≥ 0 (х – 3)(х + 3) > 0 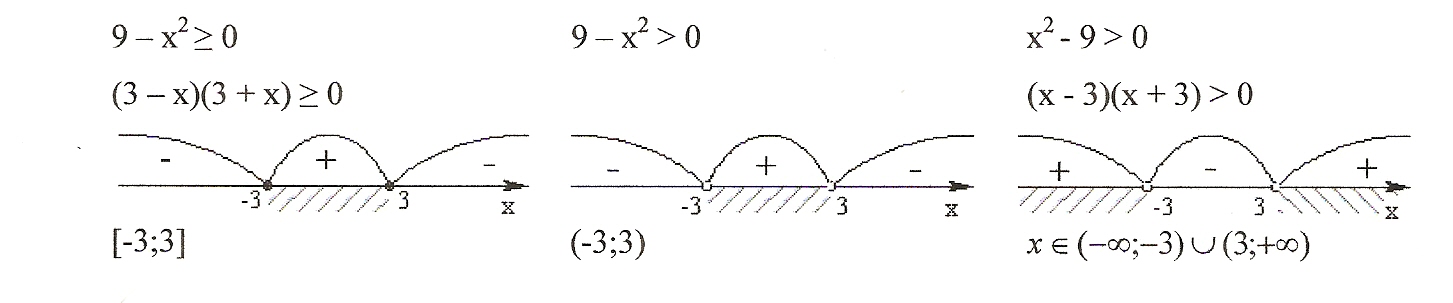 [-3;3] (-3;3) Ответ: Б.
а) найти решения неравенства Решение: нули функции 1 и Ответ: Б) Функция задана формулой у=f(x). Найдите область определения функции: Решение: Ответ: Тетради сдают на проверку.
Заключение. Таким образом, планируя урок обобщения и систематизации знаний, каждому учителю необходимо помнить о следующих структурных элементах урока [1]:
Анализ результатов мониторинга показывает положительную динамику качества знаний и умений. Работая в данном направлении на уроках математики, мне удалось добиться осознанного усвоения основных понятий, умений, алгоритмов построения параболы. Своей педагогической находкой считаю разработку блока урока по теме «Квадратичная функция» и пакета диагностических материалов к нему. Заканчивая анализ своей деятельности, приведу полученные мною результаты работы:
Литература.
|