Правила преобразования логических выражений; методы решения логических задач. Учащиеся должны уметь: применять законы логики; упрощать сложные логические выражения

Скачать 50.74 Kb. Название Правила преобразования логических выражений; методы решения логических задач. Учащиеся должны уметь: применять законы логики; упрощать сложные логические выражения Дата 18.04.2016 Размер 50.74 Kb. Тип Правила

Урок по информатике: Решение логических задач средствами алгебры логики Цели: познакомить учащихся с решением логических задач средствами алгебры логики. Задачи: Научить учащихся решать логические задачи средствами алгебры логики; Способствовать формированию логического мышления, интереса к изучаемому материалу. Ожидаемые результаты обучения: Учащиеся должны знать: законы логики; правила преобразования логических выражений; методы решения логических задач. Учащиеся должны уметь: применять законы логики; упрощать сложные логические выражения: решать логические задачи средствами алгебры логики. Ход урока I. Оргмомент. II. Проверка домашнего задания. III. Изложение нового материала. Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач: средствами алгебры логики; табличный; с помощью рассуждений. Сегодня на уроке познакомимся с решением логических задач средствами алгебры логики. Обычно используется следующая схема решения: изучается условие задачи; вводится система обозначений для логических высказываний; конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи; определяются значения истинности этой логической формулы; из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении. Задача. Представим такую ситуацию: по телевизору синоптик объявляет прогноз погоды на завтра и утверждает следующее: Если не будет ветра, то будет пасмурная погода без дождя. Если будет дождь, то будет пасмурно и без ветра. Если будет пасмурная погода, то будет дождь и не будет ветра. Так какая же погода будет завтра? Решение. Выделим простые высказывания и запишем их через переменные: А – «Ветра нет» В – «Пасмурно» С – «Дождь» Запишем сложные высказывания через введенные переменные: Если не будет ветра, то будет пасмурная погода без дождя: Если будет дождь, то будет пасмурно и без ветра: Если будет пасмурная погода, то будет дождь и не будет ветра: Запишем произведение указанных функций: Упростим формулу (используем законы де Морга, переместительный закон, закон противоречия): Приравняем результат единице, т.е. 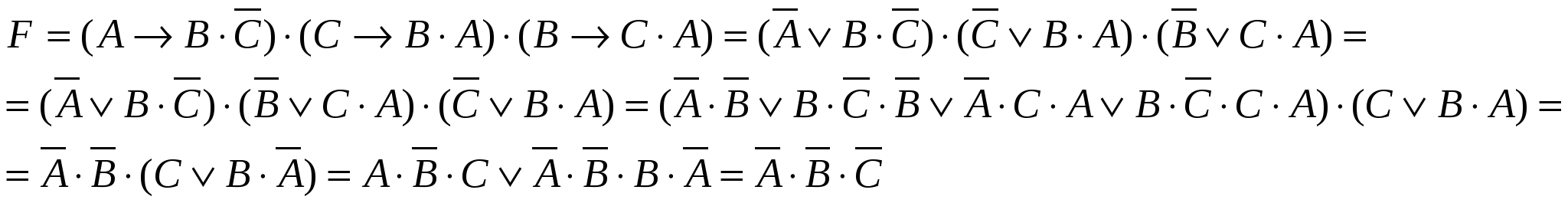наше выражение должно быть истинным: Проанализируем результат: Логическое произведение равно 1, если каждый множитель равен 1. Поэтому: Значит: А=0; В=0; С=0 Ответ: погода будет ясная, без дождя, но ветреная. IV. Закрепление изученного материала. Задача 1. В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайне мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики. Решение. Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть: А – «В первой аудитории находиться кабинет информатики»; В – «Во второй аудитории находится кабинет информатики». Отрицания этих высказываний: – «В первой аудитории находиться кабинет физики»; – «Во второй аудитории находиться кабинет физики». Высказывание, содержащееся на табличке на двери первой аудитории, соответствует логическому выражению: Высказывание, содержащееся на табличке на двери второй аудитории, соответствует логическому выражению: Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего записывается следующим образом: Подставим вместо Х и Y соответствующие формулы: Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения: В соответствии с законом непротиворечия: Упростим теперь второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания: В соответствии с законом непротиворечия: В результате получим: Для того чтобы выполнялось равенство , В и должны быть равны 1, то есть соответствующие им высказывания истинны. Ответ. В первой аудитории находится кабинет физики, а во второй - кабинет информатики. Задача 2. На вопрос «Кто из твоих учеников изучал логику?» учитель ответил: «Если логику изучал Андрей, то изучал и Борис. Однако неверно, что если изучал Семен, то изучал и Борис». Кто же изучал логику? Решение. Обозначим буквами высказывания: А — логику изучал Андрей; В — логику изучал Борис; С — логику изучал Семен. Оба высказывания учителя можно записать в виде импликаций: «Если логику изучал Андрей, то изучал и Борис». «Неверно, что если изучал Семен, то изучал и Борис». Применим логическое отрицание ко второму высказыванию и составим уравнение с помощью логического умножения: Теперь представляем импликацию через базовые операции и применяем закон де Моргана: Это уравнение имеет единственное решение: . Ответ: логику изучал только Семен. V. Итог урока. Обобщить пройденный материал, оценить работу активных учеников. VI. Домашнее задание. Задача. Кто из ребят играет в шахматы, если известно, что: если играет Андрей или Виктор, то Сергей не играет; если Виктор не играет, то играют Сергей и Дмитрий; Сергей играет.