|
Рабочая программа по алгебре (8 класс) Пояснительная записка
Рабочие программы и тематическое планирование
(2012 – 2013) Попова Н.В.
Рабочая программа по алгебре (8 класс)
Пояснительная записка
Материалы рабочей программы составлены на основе:
Федерального компонента государственного стандарта общего образования (Приказ Министерства образования от 05.03.2004 №1089;
Закона РФ «Об образовании» №122 – ФЗ в последней редакции от 01.12.2007. №313 – ФЗ;
Обязательного минимума содержания основного общего образования (Приказ Министерства образования РФ от19.05.96 №1276;
Обязательного минимума содержания основного общего и среднего (полного) общего образования (Приказ Министерства образования от 30.06.99. №56);
Примерной программы по математике основного общего образования (Из сборника «Программы общеобразовательных учреждений» М.Просвещение 2008г.);
Федерального базисного учебного плана для образовательных учреждений Российской Федерации (Приказ МО РФ от 09.03.04г.№03 – 1263);
Федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2011-12 учебный год;
Методического письма о преподавании учебных предметов в условиях введения федерального компонента государственного стандарта общего образования;
Требований к оснащению образовательного процесса в соответствии с содержанием учебных предметов компонента государственного стандарта общего образования;
Конвенции о правах ребенка.
Рекомендаций авторских программ по алгебре А.Г. Мордковича.
Согласно базисному учебному плану средней (полной) школы, рекомендациям Министерства образования Российской Федерации и в продолжение начатой в 7 классе линии, выбрана данная учебная программа и учебно-методический комплект.
Учебник: А. Г.Мордкович, Л.А.Александрова, Т. Н. Мишустина, Е.Е.Тульчинская
(часть1), задачник ( часть2).
В соответствии с федеральным базисным учебным планом для образовательных учреждений Российской Федерации на изучение алгебры в 8 классе отводится 105 часов, в неделю – 3часа.
Контрольных работ – 10, из них одна итоговая.
Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных
работ и математических диктантов.
Изучение математики на ступени основного общего образования
направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудности;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами
Требования к уровню подготовкеи учащихся, обучающихся по даннй программе.
Учащиеся должны знать/понимать:
значение математической науки для решения задач, возникающих в теории и практике;
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения, неравенства;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа;
должны уметь:
выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени;
определять область допустимых значений для дробей, сокращать, складывать и вычитать алгебраические дроби с одинаковыми и разными знаменателями, приводить дроби к наименьшему знаменателю; умножать, делить и возводить алгебраические дроби в степень; упрощать выражения и доказывать тождества;
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученные результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определения, возрастание и др.) и символику; понимать ее при чтении текста, в речи учителя, в формулировке задач;
понимать содержательный смысл важнейших свойств функций; уметь по графику функции отвечать на вопросы, касающиеся ее свойств: указывать промежутки возраста�ния и убывания, знакопостоянства, исследовать функции на монотонность;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики; уметь строить графики функций — линейной, прямой и обратной пропорциональностей, квадратичной фзункции —з в некоторых стандартных положениях, а также графики y = f(x + l), y = f(x) + m, y = f(x + l) +m, если известен график функции y = f(x);
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
Решать следующие жизненно – практические задачи:
самостоятельно приобретать и применять знания в различных ситуациях;
аргументировать и отстаивать свою точку зрения;
уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем энциклопедий и справочников для нахождения информации.
выполнять расчеты по формулам; составлять формулы, выражающие зависимости между реальными величинами;
моделировать практические ситуации и исследовать построенные модели с использованием аппарата алгебры;
использовать приобретенные знания для интерпритации графиков реальных зависимостей между величинами.
Содержание учебного материала
Алгебраические дроби (21ч)
Понятие алгебраической дроби. Основное свойство алгебраической дроби. Сокращение алгебраических дробей. Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений (первые представления). Степень с отрицательным целым показателем.
Основная цель – выработать умение выполнять преобразования алгебраических дробей. Изучение темы начинается с введения понятия алгебраической дроби, её числового значения и допустимых значений, входящих в неё букв.
Функция у =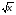 . Свойства квадратного корня (18ч) . Свойства квадратного корня (18ч)
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел.
Функция у= , ее свойства и график. Выпуклость функции.
Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби. Модуль действительного числа. График функции у=/х/.Формула =/х/.з
Основная цель – систематизировать сведения о рациональных числах, ввести понятие иррационального и действительного чисел. Научить выполнять простейшие преобразования выражений, содержащих квадратные корни
Квадратичная функция. Функция у =к/х (18ч)
Квадратичная функция. Функция у=k/х
Функция у=kх2, её свойства и график. Функция у=k/х, её свойства и график. Как построить график функции у=f(х+l)+m, если известен график функции у=f(х). Функция у=ах2+bх+с, её свойства и график. Графическое решение квадратных уравнений. Дробно-линейная функция, её свойства и график. Как построить графики функций у=│f(х)│и у=f│х│, если известен график функции у=f(х).
Основная цель – научить строить график функции обратной пропорциональности, применять свойства функции 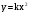 при решении упражнений. В данной теме рассматриваются упражнения на свойства и график функции при решении упражнений. В данной теме рассматриваются упражнения на свойства и график функции 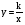 и на построение графика функции y = f(x + m) + n, если известен график функции у=f(х). и на построение графика функции y = f(x + m) + n, если известен график функции у=f(х).
Квадратные уравнения (21ч)
Основные понятия, связанные с квадратными уравнениями. Формулы корней квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на линейные множители. Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной .Рациональные уравнения как математические модели реальных ситуаций. Частные случаи формулы корней квадратных уравнений.
Иррациональное уравнение. Метод возведения в квадрат.
Основная цель – выработать умения решать квадратные уравнения, уравнения, сводящиеся к квадратным уравнениям, и применять их к решению задач. В данной теме рассматриваются примеры решения уравнений с параметрами.
Неравенства (15ч)
Свойства числовых неравенств. Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенств.
Квадратное неравенство. Алгоритм решения квадратного неравенства.
Возрастающая функция. Убывающая функция. Исследование функций на монотонность з(с использованием свойств числовых неравенств).
Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.
Линейные неравенства. Квадратные неравенства. Доказательство неравенств. Приближённые вычисления. Стандартный вид положительного числа.
Основная цель – сформировать умение решать неравенства первой степени с одной переменной и квадратные неравенства с помощью графика квадратичной функции и методом интервалов.
Обобщающее повторение (12ч)
Литература
Для учителя:
Программы. Математика. 5-6 классы. Алгебра 7-9 классы. Алгебра и начала математического анализа. 10-11 классы/авт.-сост. И.И.Зубарева, А.Г.Мордкович. М.: «Мнемозина», 2010 г.
А. Г. Мордкович. Алгебра. 8 класс. В 2 ч. Часть 1. Учебник. М.: «Мнемозина», 2008г.
А. Г. Мордкович, Л.А.Александрова, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра. 8 класс. В 2 ч. Часть 2. Задачник. М.: «Мнемозина», 2008г.
А. Г. Мордкович. Алгебра. 8 класс. Методическое пособие для учителя. М.: «Мнемозина», 2010 г.
Л.А.Александрова. Алгебра. 8 класс. Самостоятельные работы. Под ред. А. Г. Мордковича. М.: «Мнемозина», 2010 г.
Л.А.Александрова. Алгебра. 8 класс. Контрольные работы. Под ред.А. Г. Мордковича. М.: «Мнемозина», 2010 г.
А. Г. Мордкович, Е.Е. Тульчинская. Алгебра. 7-9 классы. Тесты для учащихся общеобразовательных учреждений. М.: «Мнемозина», 2009 г.
В.В. Шеломовский. Электронное сопровождение курса «Алгебра-8» / Под ред.А. Г. Мордковича.
9.Интернет – ресурсы.
Для обучающихся:
А. Г. Мордкович. Алгебра. 8 класс. В 2 ч. Часть 1. Учебник. М.: «Мнемозина», 2008 г.
А. Г. Мордкович, Л.А.Александрова, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра. 8 класс. В 2 ч. Часть 2. Задачник. М.: «Мнемозина», 2008 г.
Л.А.Александрова. Алгебра. 8 класс. Самостоятельные работы. Под ред. А. Г. Мордковича. М.: «Мнемозина», 2010 г.
А. Г. Мордкович, Е.Е. Тульчинская. Алгебра. 7-9 классы. Тесты для учащихся общеобразовательных учреждений. М.: «Мнемозина», 2009 г.
5.Интернет – ресурсы.
Для родителей:
1Домашняя работа по алгебре за 8 класс к задачнику «Алгебра,8класс. В2 ч.Ч 2. Задачник для учащихся общеобразовательных учреждений (А. Г.Мордкович, Л.А. Александрова, Т.Н.Мишустина и др.); под редакцией А.Г.Мордковича, - 11-е изд., стереотип. – М.:Мнемозина,2009г.
2.Интернет – ресурсы. |
|
|
 Скачать 101.64 Kb.
Скачать 101.64 Kb.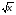 . Свойства квадратного корня (18ч)
. Свойства квадратного корня (18ч)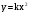 при решении упражнений. В данной теме рассматриваются упражнения на свойства и график функции
при решении упражнений. В данной теме рассматриваются упражнения на свойства и график функции 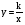 и на построение графика функции y = f(x + m) + n, если известен график функции у=f(х).
и на построение графика функции y = f(x + m) + n, если известен график функции у=f(х).