Семинар в 10 ф-м классе по теме " Тригонометрические уравнения" Цели: Обобщить и систематизировать материал по теме "Решение тригонометрических уравнений"
 Скачать 97.11 Kb. Скачать 97.11 Kb. |
| Урок-семинар в 10 ф-м классе по теме " Тригонометрические уравнения" Цели:
Содержание темы. Исследование и решение тригонометрических уравнений, в которых требуется установить способ решения. Тип урока. Урок обобщения и систематизации знаний. Форма урока. Урок-семинар Организационные формы общения. Групповая, индивидуальная. Структура урока:
Ход урока Мотивационная беседа. Решая тригонометрические уравнения, мы использовали различные способы. Их немало, повторим некоторые. На сегодняшнем уроке нам предстоит исследование и решение тригонометрических уравнений, в которых требуется установить:
Актуализация опорных знаний. Устно среди уравнений (слайд)
выбрать те, которые решаются: а) заменой переменной; б) делением на старшую степень синуса или косинуса, т. е. как однородные; в) понижением степени; г) с помощью формул суммы или разности; д) методом вспомогательного угла (аргумента); е) с помощью формул произведения; ё) методом универсальной подстановки; ж) разложение на множители.
Задание учащимся:
Учащимся предлагается из данных уравнений выбрать способы решения тригонометрических уравнений:
Что еще нужно учитывать при решении тригонометрических уравнений? Возможны случаи когда появляются посторонние корни. Например при решении уравнения 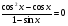 появляются посторонние корни. появляются посторонние корни. Диагностика. После повторения основ решения тригонометрических уравнений проверим ваше умение исследовать и решение тригонометрических уравнений, в которых требуется установить, при каких значениях параметра а уравнение имеет решения или не имеет их. Вам предлагаются следующие задания:
Первое уравнение решаем вместе, рассуждая, дополняя друг друга.
Поделим обе части уравнения на 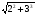 = =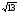 , получим , получим 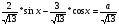 . Так как . Так как 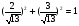 , то, обозначая , то, обозначая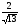 = cosφ, = cosφ,  = sinφ, приведем уравнение к виду = sinφ, приведем уравнение к видуsin(х – φ) = 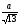 , где φ = arctg3/2. Из условия |sin(х – φ)|≤1 получаем , где φ = arctg3/2. Из условия |sin(х – φ)|≤1 получаем |а|≤ 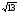 . .Ответ: а Є [- 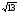 ; ;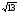 ]. ].Над решением второго уравнения работаем парами, потом обменяемся идеями. Правильное решение спроецируем на экран.
Поделим обе части уравнения на 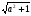 , получим , получим 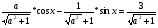 , где sinφ = , где sinφ =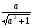 cosφ = 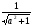 отсюда, sin (х – φ) = отсюда, sin (х – φ) = 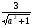 Из условия Из условия 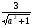 ≤1 имеем a2+ 1≥9, значит,|а|≥2√2. ≤1 имеем a2+ 1≥9, значит,|а|≥2√2.Ответ: а Є(-∞,-2√2]∪[ 2√2,+∞). Вспомним решения уравнений 2 и 8 из устной работы, используем навыки при работе с третьим уравнением.
Используя формулу sin2x + cos2x = 1, получим, 1 - cos2x - 5 cosx + а = 0. После замены cosx = t уравнение примет вид f (t) = 0, где До этого момента в работу детей вмешиваться не надо. Остальное необходимо разбирать совместно, привлекая рисунки параболы. f (t) = t2+ 5 t – (а + 1 ) абсцисса вершины параболы у = t2+ 5 t – (а + 1 ) t = -5/2 не принадлежит [-1;1], следовательно, уравнение f (t) = 0 на отрезке [-1;1] может иметь не более одного корня. Искомые значения а находим из неравенства f (-1)* f (1) ≤ 0, значит, (-5- а) (5 – а) ≤ 0. Ответ: а Є [-5;5]. Самостоятельная работа. Вариант №1 – решить уравнения 2;4;5;6;10 Вариант №2 – 1;3;7;8;9 Подведение итогов урока Мы замечательно поработали. Те навыки, которые вы получили на уроке, помогут нам в дальнейшей работе. А чтобы вы их не потеряли, но продолжили развивать выполните дома следующие задания. Домашнее задание. Выясните, при каких значениях параметра а уравнения имеют решения:
При каких значениях параметра а уравнения не имеют решений.
Решение самостоятельной работы а) Приведением к квадратному и заменой переменной решаются уравнения 4, 8. 4.sin2x - 2sinx – 3 = 0 пусть sinx = t, тогда t2+ 2 t – 3 = 0, где t = -3; 1. Учитывая, что |sinх|≤1, а -3<-1, имеем sinx = 1, Х =π/2+2 π n, n Є Z. Ответ: π /2+2 πn, n Є Z. 8.3sin2x + 2cos2x +2 cosx = 0 sin2x = 1 - cos2x, значит, 3 - 3cos2x + 2cos2x +2cosx = 0, cos2x - 2cosx – 3 = 0, пусть cosx = t, тогда t2- 2 t – 3 = 0, где t = 3; -1 3>1, значит, cosx = -1, Х = π + 2 π n, n Є Z. Ответ: π + 2 π n, n Є Z. б) Делением на старшую степень решаются уравнения 1, 5, 9. 1.2sin2x - 5cos2x = 3sinxcosx Разделив каждое слагаемое на cos2x,получим. 2tg2х - 3tgх - 5 = 0, Пусть tgх = p, тогда 2p2 - 3p - 5 = 0, где p = 2,5; -1, tgх =2,5, х = arctg2,5 + πn, n Є Z; tgх = -1, х = -π /4 + π n, n Є Z. Ответ: arctg2,5 + π n, n Є Z; -π /4 + π n, n Є Z. 5.√2 cosx – sinx = 0 |: cosx, cosx≠0, tgх = √2, х = arctg√2 + πn, n Є Z ответ: arctg√2 + π n, n Є Z 9.sin2x - √3/ 3sin2x = cos2x |: cos2x, cosx≠0 tg2х - √3/3 tg x- 1 = 0, tgх = √3/6(1 ± √13), х = arctg √3/6(1 ± √13)+ π n, n Є Z; ответ: arctg √3/6(1 ± √13)+ π n, n Є Z в) Понижение степени используют при решении уравнения 2. 2.sin2x + cos22x = 3/2. sin2x + 1/2(1 +cosx) =3/2, 2 sin2x + 1 +cosx -3 = 0, 2 - 2 cos2x + 1 +cosx -3 = 0, 2 cos2x - cosx = 0, cosx(2 cosx – 1) = 0, cosx = 0 или cosx = 1/2 Х = π /2 + π n, n Є Z или Х = ± π /3 + 2 π n, n Є Z. Ответ: ± π /3 + 2 π n, n Є Z; π /2 + π n, n Є Z. г) С помощью формул суммы или разности решаются уравнения 6, 7. 6.sinx + sin3x = sin5x – sinx 2 sin2x cosx - 2 sin2x cos3x = 0, sin2x (cosx - cos3x) = 0, sin22x sinx = 0, sin2x = 0 или sinx = 0, Х = π /2 n, n Є Z или Х = π n, n Є Z. Объединив множества, получим, Х = π /2 n, n Є Z Ответ: π /2 n, n Є Z д) Методом вспомогательного аргумента, который состоит в преобразовании выражения asinx ± bcosx к виду √(a2 + b2) sin(x±φ), где φ = b/√(a2 + b2) решается уравнение 10. 7.sinx + cosx = 1. Учитывая, что a= 1, b = 1, получим уравнение √2 sin(x+φ) = 1, где φ = arcsin√2/2, sin(x+ φ /4) = √2/2, х = - π /4 + (-1) π /4+ π n, n Є Z. Ответ: - π /4 + (-1) π /4+ π n, n Є Z. Рефлексия. С учащимися обсуждается работа на уроке; выясняется, что нового узнали. Вопросы к семинару.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||